5.3: Colapso hidrófobo

Colapso hidrófobo ¹

Vemos que las partículas hidrofóbicas en el agua intentarán minimizar su área superficial con el agua mediante la agregación o separación de fases. Este proceso, conocido como colapso hidrofóbico, se considera el efecto dominante que impulsa el plegamiento de las proteínas globulares.

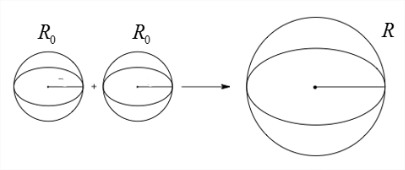
Calculemos el cambio de energía libre para dos gotas de aceite que se unen en una sola. Las gotitas más pequeñas tienen un radio R ₀ y la gotita final un radio de\(R\).

\[\Delta G_{\text{collapse}} = \Delta G_{\text{sol}} (R) - 2 \Delta G_{\text{sol}} (R_0) \nonumber\]

El volumen total de petróleo es constante, solo cambia el área superficial. Si el área de superficie inicial total es\(A_0\), y la superficie total final es\(A\), entonces

\[\Delta G_{\text{collapse}} = (A - A_0) \gamma \nonumber\]

que siempre es negativo desde entonces\(A < A_0\) y\(\gamma\) es positivo.

Esto descuida el cambio en la entropía traslacional debido a que dos gotas se unen en una sola. Considerando solo los grados de libertad traslacionales de las gotas, esto debería ser aproximadamente\(\Delta S_{\text{collapse}} \approx k_B \ln (3/6)\). En otras palabras, un número pequeño comparado con el término de superficie.

Podemos generalizar esto fácilmente a una cadena de\(n\) cuentas, cada una de radio\(R_0\), que colapsan hacia una sola esfera con el mismo volumen total. En este caso, consideremos cómo varía la energía libre del sistema con el número de cuentas que se han unido.

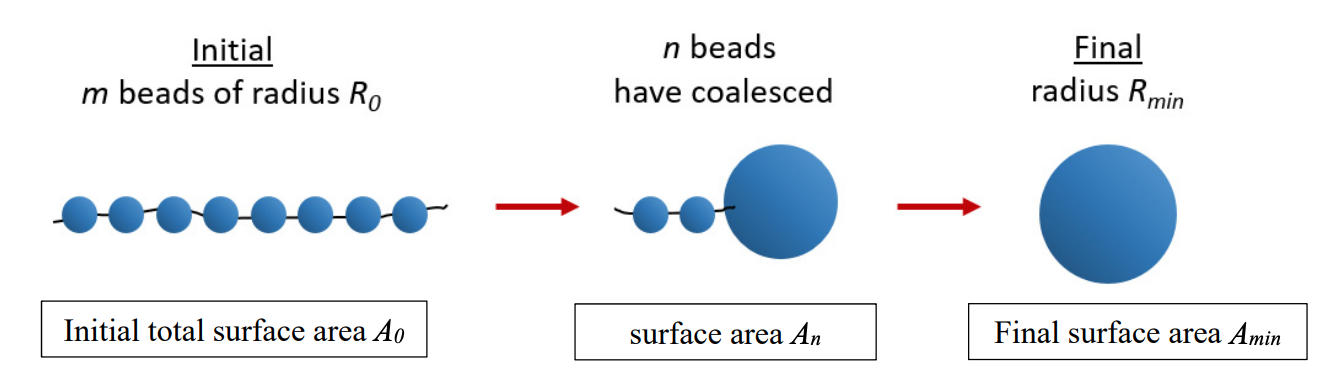
Nuevamente el volumen total es constante,\(V=n\left(\dfrac{4}{3} \pi R_{0}^{3}\right)\) y la superficie cambia. El área superficial inicial es\(A_{0}=m 4 \pi R_{0}^{2}\) y la superficie final es\(A_{\min }=4 \pi \left (R_{\min } \right)^{2} = m^{2/3} 4 \pi R_{0}^{2}\). A lo largo del camino, hay una caída de la superficie total por cada perla que se fusiona. Consideremos un camino, en el que una cuenta individual se fusiona con una gota en crecimiento. La superficie total una vez que\(n\) las\(m\) partículas se han unido es

\(A_n\)= (área superficial de gota formada por perlas\(n\) coalescentes) + (área total de\(m-n\) perlas restantes)

\[\begin{array} {rcl} {A_n} & = & {(n^{2/3} 4\pi R_0^2) + (m - n) 4\pi R_0^2} \\ {} & = & {(m + n^{2/3} - n)4\pi R_0^2} \\ {} & = & {A_0 + (n^{2/3} - n)4\pi R_0^2} \end{array}\nonumber\]

El cambio de energía libre para las\(n\) cuentas coalescentes es

\[\begin{array} {rcl} {\Delta G_{\text{coll}}} & = & {(A_n - A_0) \gamma } \\ {} & = & {(n^{2/3} - n) 4\pi R_0^2 \gamma} \end{array} \nonumber\]

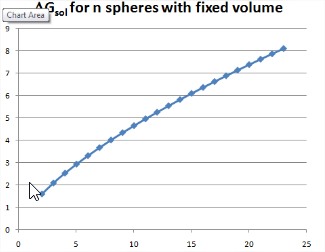
Esta energía libre se representa como una función del número de cuentas a un volumen fijo. Este es un paisaje energético que ilustra que la dirección cuesta abajo del cambio espontáneo conduce a un menor número de cuentas. La fuerza impulsora para el colapso de esta cadena puede considerarse como la disminución de la energía libre en función del número de cuentas en la cadena:

\[\begin{array} {c} {f_{\text{coll}} = -\dfrac{\partial \Delta G_{\text{coll}}}{\partial r} \propto - \dfrac{\partial \Delta G_{\text{coll}}}{\partial n}} \\ {-\dfrac{\partial \Delta G_{\text{coll}}}{\partial n} = 4\pi R_0^2 \gamma \left (1 - \dfrac{2}{3} n^{-1/3} \right )} \end{array} \nonumber\]

Esta no es una fuerza real expresada en Newtons, pero podemos pensarla como una pseudo-fuerza, con el número de cuentas actuando como un proxy para la extensión de la cadena. Si quieres extender una cadena hidrofóbica, debes trabajar en contra de esto. Escrito en términos de la extensión de la cadena\(x\) (no el área de caída\(A\))

\[w=-\int_{x_{0}}^{x} f_{ext} d x = \int_{x_{0}}^{x} \left (\dfrac{\partial \Delta G_{coll}}{\partial A_{n}}\right) \left(\dfrac{\partial A_{n}}{\partial x}\right) d x\nonumber\]

Aquí todavía tenemos que averiguar la relación entre extensión y superficie,\(\partial A_{n} / \partial x\).

Alternativamente, podemos pensar en la coordenada de colapso como el número de cuentas coalescentes,\(n\).

Colapso hidrófobo y fluctuaciones de forma

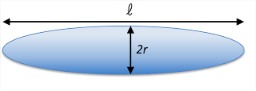
Un enfoque alternativo para pensar sobre este problema es en términos del colapso de un elipsoide prolado a una esfera ya que se busca minimizar su superficie. Tomamos el elipsoide para tener un largo\(\ell /2\) y un radio corto\(r\). El área y el volumen son entonces:

\ [
\ begin {array} {l}
A=2\ pi\ left (r^ {2} +\ frac {\ ell^ {2}} {4}\ frac {\ alpha} {\ tan\ alpha}\ derecha)\ quad\ alpha=\ cos ^ {-1}\ left (\ frac {2 r} {\ ell}\ right)\\
V=\ frac {2} {3}\ pi r^ {2}\ ell\ quad (\ text {constante})\\
\ por lo tanto\ quad r^ {2} =3 V/2\ pi\ ell\
A=\ izquierda (\ frac {3 V} {\ ell} +\ pi\ frac {\ ell^ {2}} {2}\ frac {\ alpha} {\ tan\ alpha}\ derecha)
\ end {array}
\ nonumber\]

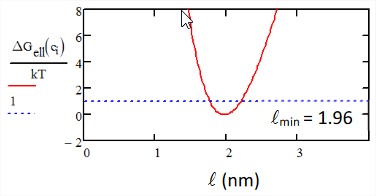
Vamos a trazar la energía libre de este elipsoide en función de\(\ell\). Para\(V = 4\ nm^3\),\(k_B T = 4.1\ pN/nm\) nos encontramos\(\ell_{\min} = 1.96\ nm\). Tenga en cuenta que en\(k_B T\) las dimensiones del elipsoide puede fluctuar sobre muchos\(\sim 5 \mathring{A}\).

Lecturas

1. N. T. Southall, K. A. Dill y A. D. J. Haymet, Una visión del efecto hidrofóbico, J. Phys. Chem. B 106, 521—533 (2002).
2. D. Chandler, Interfaces y la fuerza impulsora del ensamblaje hidrofóbico, Nature 437, 640—647 (2005).
3. G. Hummer, S. Garde, A. E. García, M. E. Paulaitis y L. R. Pratt, Efectos hidrofóbicos a escala molecular, J. Phys. Chem. B 102, 10469—10482 (1998).
4. B. J. Berne, J. D. Weeks y R. Zhou, Deshumectación e interacción hidrofóbica en sistemas físicos y biológicos, Annu. Rev. Phys. Chem. 60, 85—103 (2009).

____________________________________________

1. Véase K. Dill y S. Bromberg, Fuerzas Impulsoras Moleculares: Termodinámica Estadística en Biología, Química, Física y Nanociencia. (Taylor & Francis Group, Nueva York, 2010), p. 675.