6.6: Teoría Debie-Hückel
- Page ID
- 69715
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Al ser no lineal, no es fácil resolver el PBE, pero para ciertos tipos de problemas, podemos hacer aproximaciones para ayudar. La aproximación Debie-Hückel se mantiene para pequeñas condiciones de potencial electrostático o de alta temperatura de manera que
\[\dfrac{ze\Phi}{k_B T} \ll 1 \nonumber\]
Este es el régimen en el que la entropía de mezcla domina las interacciones electrostáticas entre iones. En este límite, podemos expandir el exponencial en eq. (6.5.5) como\(\exp [-ze \Phi /k_B T] \approx 1 - ze \Phi /k_B T\). El término principal en la suma resultante cae debido a la condición de neutralidad de carga, eq. (6.5.4). Mantener el segundo término en la expansión lleva a
\[\nabla^2 \Phi = \kappa^2 \Phi \label{eq6.6.1}\]
donde
\[\kappa^2 = \dfrac{2e^2}{\varepsilon k_B T} I \nonumber\]
y la fuerza iónica,\(I\), se define como
\[I = \dfrac{1}{2} \sum_i C_{0, i} z_i^2 \nonumber\]
Mirando la eq. (\(\ref{eq6.6.1}\)), vemos que la aproximación Debie-Hückel linealiza el PBE. Se le conoce como la ecuación de Debie-Hückel, o la PBE linealizada. Para el caso de la solución 1:1 de electrolito descrita por la eq., nuevamente obtenemos la eq. (\(\ref{eq6.6.1}\)) usando\(\text{sinh} (x) \approx x\) como\(x \to \infty\), con
\[\kappa^2 = \dfrac{2z^2 e^2 C_0}{\varepsilon k_B T} = 8\pi z^2 C_0 \ell_B \nonumber\]
La constante\(\kappa\) tiene unidades de distancia inversa, y su inversa se conoce como la longitud de Debye\(\lambda_D = \kappa^{-1}\). La longitud de Debye establece la escala de distancia sobre la que decae el potencial electrostático, es decir, la distancia sobre la cual las cargas se apantallan entre sí. Para los electrolitos simétricos
\[\lambda_D = \kappa^{-1} = \sqrt{\dfrac{\varepsilon k_B T}{2z^2 e^2 C_0}}\]
Como ejemplo: 1:1 electrolitos en\(\text{H}_2\text{O}\):\(\varepsilon = 80\);\(z_+ = -z_- = 1\);\(T = 300\ K\) conduce a
\[\begin{array} {ll} {C_0 = 100\ mM} & {\lambda_D = 9.6\ \mathring{A}} \\ {C_0 = 10\ mM} & {\lambda_D = 30.4\ \mathring{A}} \end{array} \nonumber\]
\[\lambda_D (\mathring{A}) \approx 3.04 \cdot [C_0 (M)]^{-1/2} \nonumber\]
La aproximación de Debye se mantiene para pequeños potenciales electrostáticos en relación con\(k_B T (r > \lambda_D)\). Por ejemplo, está bien para la distribución de iones sobre proteínas grandes o vesículas pero no para el agua en una bolsa de unión.
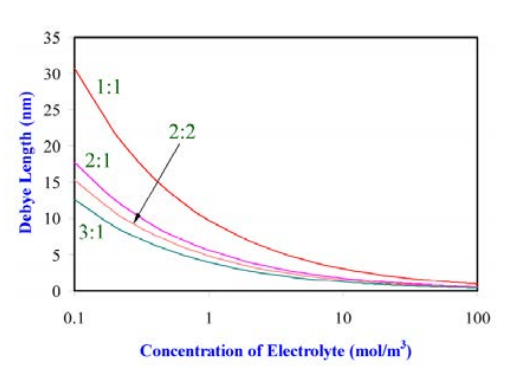
La variación de la longitud de Debye con concentraciones de electrolitos. Reimpreso de P. Ghosh http://nptel.ac.in/courses/103103033/module3/ lecture3.pdf.

