11.1: Caminata Aleatoria y Difusión

Queremos describir la correspondencia entre una imagen microscópica para el recorrido aleatorio de partículas y la difusión macroscópica de gradientes de concentración de partículas. Describiremos las estadísticas para la ubicación de un andador aleatorio en una dimensión (x), que se permite recorrer una distancia Δx a la derecha (+) o izquierda (—) durante cada intervalo de tiempo Δt. En cada momento se debe dar un paso a la izquierda o a la derecha, y los pasos a izquierda y derecha son igualmente probables.

Comencemos describiendo dónde se encuentra el sistema después de dar n pasos cualitativamente. Podemos relacionar la posición del sistema con donde estaba antes de dar un paso escribiendo:

\[x(n) = x(n-1) \pm \Delta x \nonumber \]

Esta expresión se puede promediar a lo largo de muchos pasos:

\[ \begin{aligned} \langle x(n) \rangle &= \langle x(n-1) \pm \Delta x \rangle \\ &= \langle x(n-1) \rangle = \langle x(n-2) \rangle = ... = \langle x(0) \rangle \end{aligned} \]

Dado que hay igual probabilidad de moverse hacia la izquierda o hacia la derecha con cada paso, el término ±Δx promedia a cero, y\(\langle x \rangle\) no cambia con el tiempo. La posición más probable para cualquier momento siempre será el punto de partida.

Consideremos ahora la varianza en el desplazamiento:

\[ \begin{aligned} \langle x^2(n)\rangle &= \langle x^2(n-1) \pm 2 \Delta x \, x(n-1)+(\Delta x )^2\rangle \\ &= \langle x^2(n-1) \rangle + (\Delta x)^2 \end{aligned} \]

En la primera línea, el término medio promedia a cero, y la varianza gana un factor de Δx ². Repitiendo este proceso para cada paso posterior sucesivo muestra que el desplazamiento cuadrático medio crece linealmente en el número de pasos.

\[ \begin{aligned} &\langle x^2(0) \rangle =0 \\ &\langle x^2(1) \rangle = (\delta x)^2 \\ &\langle x^2(2) \rangle = 2(\delta x )^2 \end{aligned} \]

\[ \vdots \nonumber \]

\[ \langle x^2 (n)\rangle = n(\Delta x)^2 \]

Cualitativamente, estos argumentos indican que las estadísticas de un andador aleatorio deben tener la misma media y varianza que la distribución de concentración para la difusión de partículas desde una posición inicial.

Función de distribución aleatoria de pasos

Ahora veamos esto un poco más cuidadosamente y describamos la distribución de probabilidad para la posición de las partículas después de n pasos, que equiparamos con el número de posibles trayectorias de caminata aleatorias que pueden conducir a un desplazamiento particular. ¿Cuál es la probabilidad de comenzar en x ₀ = 0 y alcanzar el punto x después de n saltos separados por el intervalo de tiempo Δt?

Similar a nuestra discusión sobre el polímero de caminata aleatoria, podemos expresar el desplazamiento de un saltador aleatorio al número total de saltos en la dirección positiva n ₊ y en la dirección negativa n _—. Si hacemos n saltos totales, entonces

\[ n = n_++n_- \qquad \longrightarrow \qquad t=n \Delta t \nonumber \]

El número total de pasos n es también nuestro proxy para el tiempo de una trayectoria dada, t. La distancia entre la posición inicial y final está relacionada con la diferencia en + y ‒ pasos:

\[ m = n_+-n_- \qquad \longrightarrow \qquad x=m\Delta x \nonumber \]

Aquí m es nuestro proxy para el desplazamiento total x. Nota de estas definiciones podemos expresar n ₊ y n _— como

\[ n_{\pm} = \dfrac{n\pm m}{2} \]

El número de diferentes formas de hacer n saltos con la restricción de n+ saltos positivos y n— negativos es

\[ \Omega = \dfrac{n!}{n_+!n_-!} \nonumber \]

La probabilidad de observar una secuencia particular de n “+” y “—” saltos es\( P(n) = (P_+)^{n_+} (P_-)^{n_-} = (1/2)^n\).

El número total de trayectorias que son posibles con n igualmente probablemente saltos “+” y “‒” es 2 ⁿ, por lo que la probabilidad de que cualquier secuencia de n pasos termine en la posición m viene dada por Ω/2 ⁿ o

\[ \begin{aligned} P(m,n) &= \left( \dfrac{1}{2} \right)^n \dfrac{n!}{n_+!n_-!} \\ &= \left( \dfrac{1}{2} \right)^n \dfrac{n!}{\dfrac{n+m}{2}! \dfrac{n-m}{2}!} \end{aligned} \]

Esta es la función binomial de distribución de probabilidad. Mirando el siguiente ejemplo para veinte pasos, vemos\(\langle m\rangle =0\) y para una distribución de probabilidad discreta que tiene una envolvente gaussiana.

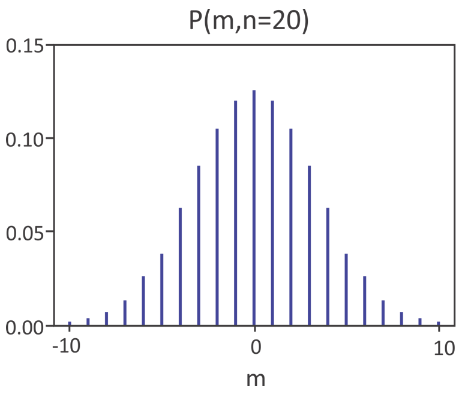
Para n muy grandes, la función de distribución se vuelve continua. Para ver esto, vamos a aplicar la aproximación de Stirling,\( n! \approx (n/e)^n \sqrt{2\pi n} \), y después de un poco de manipulación encontramos ¹

\[P(m,n) = \sqrt{\dfrac{2}{\pi n}} e^{-m^2/2n} \]

Tenga en cuenta que esta distribución tiene una envolvente que sigue una distribución gaussiana normal para una variable continua donde la varianza σ ² es proporcional al número de pasos n.

Para expresar esto con una variable de tiempo, insertamos n = T/δT y m = X/δx en eq. (11.1.3) para obtener la función de distribución de probabilidad discreta:

\[ P(x,t) = \sqrt{\dfrac{\Delta t}{2\pi t}} \exp \left[ - \dfrac{\Delta t x^2}{2t(\Delta x)^2} \right] \nonumber \]

Tenga en cuenta que podemos reescribir esta distribución de probabilidad discreta similar a la
solución de difusión continua

\[ P(x,t) = \sqrt{\dfrac{(\Delta x)^2}{4\pi Dt}}e^{-x^2/4Dt} \]

si equiparamos la varianza y la constante de difusión como

\[D = \dfrac{(\Delta x )^2}{2\Delta t} \nonumber \]

La ecuación (11.1.4) es ligeramente diferente porque P es una probabilidad sin unidades para encontrar la partícula entre x y X+δX, en lugar de una densidad de probabilidad continua ρ con unidades de m ^-1: ρ (x, t) dx = P (x, t). Aun así, la ecuación (11.1.4) sugiere que la función de distribución de probabilidad dependiente del tiempo para la caminata aleatoria obedece a una ecuación de difusión

\[ \dfrac{\partial P}{\partial t} = \Delta x D \dfrac{\partial^2 P}{\partial x^2} \qquad \qquad or \qquad \qquad \dfrac{\partial \rho}{\partial t} = D \dfrac{\partial^2 \rho}{\partial x^2} \]

Caminata aleatoria tridimensional

Podemos extender este tratamiento a la difusión desde una fuente puntual en tres dimensiones, usando un paseo aleatorio de n pasos de longitud Δx sobre una celosía cúbica 3D. Los pasos se dividen en los que se toman en las direcciones x, y y z:

\[ n = n_x+n_y+n_z \nonumber \]

y la distancia del andador desde el origen se obtiene a partir del desplazamiento neto a lo largo de los ejes x, y y z:

\[r = (x^2+y^2+z^2)^{1/2} = m\Delta x \\ m = \sqrt{m_x^2+m_y^2+m_z^2} \nonumber \]

Por cada intervalo de tiempo el andador da un paso eligiendo la dirección positiva o negativa a lo largo de los ejes x, y y z con igual probabilidad. Dado que cada dimensión es independiente de las demás

\[ P(r,n) = P(m_x,n_x)P(m_y,n_y)P(m_z,n_z) \nonumber \]

Mirando el desplazamiento radial desde el origen, encontramos

\[ \sigma_x^2 + \sigma_y^2 + \sigma_z^2 = \sigma_r^2 \nonumber \]

donde

\[ \sigma_x^2 = \dfrac{(\Delta x )^2t}{\Delta t} \rightarrow 2D_xt \nonumber \]

pero ya que cada dimensión es igualmente probable\(\sigma_r^2 = 3\sigma_x^2 \). Luego usando la eq. (11.1.3)

\[ P(r,t) = \left( \dfrac{3\Delta x^2}{2\pi \sigma_r^2} \right)^{3/2} e^{-3r^2/2\sigma_r^2} \nonumber \]

donde\(\sigma_r^2=6Dt\).

__________________________________________________

1. M. Daune, Biofísica Molecular: Estructuras en Movimiento. (Oxford University Press, Nueva York, 1999), Capítulo 7.