11: Movimiento browniano

El movimiento browniano se refiere a los movimientos aleatorios de pequeñas partículas bajo excitación térmica en solución descritos por primera vez por Robert Brown (1827), ¹ quien con su microscopio observó el movimiento espacial aleatorio y nervioso de los granos de polen en el agua. Este fenómeno está intrínsecamente vinculado con la difusión. La difusión es la realización macroscópica del movimiento browniano de las moléculas dentro de los gradientes de concentración. La base teórica para esta relación fue descrita por Einstein en 1905, ² y Jean Perrin ³ proporcionó los experimentos detallados que confirmaron sus predicciones.
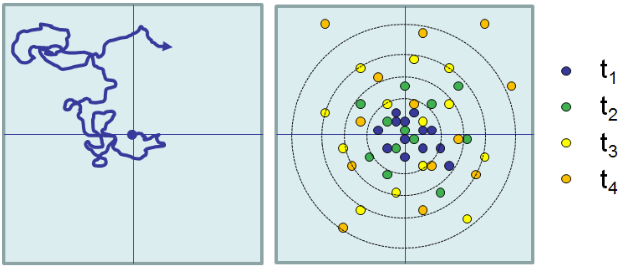
Dado que el movimiento de cualquier partícula es único, el movimiento browniano debe describirse estadísticamente. Observamos que el desplazamiento cuadrático medio de una partícula promediada en muchas mediciones crece linealmente con el tiempo, al igual que con la difusión.

El factor de proporcionalidad entre el desplazamiento medio cuadrado y el tiempo es la constante de difusión en la Segunda Ley de Fick. En cuanto a la difusión, el factor de proporcionalidad depende de la dimensionalidad. En 1D, si\(\langle x^2(t) \rangle /t = 2D \) entonces en 3D\( \langle r^2(t) \rangle /t = 6D \), donde D es la constante de difusión.

El movimiento browniano es una propiedad de las moléculas en equilibrio térmico. Se aplica a una partícula más grande (es decir, una proteína) que experimenta un desequilibrio de muchas fuerzas microscópicas ejercidas por muchas moléculas muy pequeñas de los alrededores (es decir, agua). La agitación térmica se origina dividiendo la energía cinética del sistema en promedio como k _B T/2 por grado de libertad. La libre difusión implica movimiento que solo está limitado por la energía cinética.

El movimiento browniano se aplica a un rango específico de fuerzas y masas donde la energía térmica (k _B T (300 K) = 4.1 pN nm) puede tener una influencia significativa en una partícula. Veamos la energía cinética traslacional promedio:

\( \left< \dfrac{mv_x^2}{2} \right> = \dfrac{1}{2}k_BT \)

Para una proteína de ~10 kDa con masa ~10 ^—23 kg, la velocidad media cuadrática debida a la energía térmica es\(v_{rms} = \langle v_x^2 \rangle^{1/2}\) = 20 m/s. para agua a 300 K, D ~10 ^—5 cm ² /s. La misma proteína tiene un desplazamiento neto en un segundo de\(x_{rms}=\langle x^2 \rangle ^{1/2}=\sqrt{2Dt} \approx 50 \, \mu \text{m}\). La gran diferencia en estos valores indica el gran número de colisiones aleatorias que experimenta esta partícula durante un segundo de evolución: (v _rms\(\cdot\) 1seg) /x _rms ≈ 4×10 ⁵. Para la proteína, las velocidades y desplazamientos son una fuerza dominante en la escala molecular. En comparación, una masa de 1 kg con k _B T de energía tendrá v _rms ~ 10 ^—11 m/s, ¡y un desplazamiento igualmente insignificante!