11.2: Cadena de Markov y Procesos Estocásticos

Trabajando nuevamente con el mismo problema en una dimensión, intentemos escribir una ecuación de movimiento para la distribución de probabilidad de caminata aleatoria:\(P(x,t)\).

• Este es un ejemplo de un proceso estocástico, en el que la evolución de un sistema en tiempo y espacio tiene una variable aleatoria que necesita ser tratada estadísticamente.
• Como antes, el movimiento de un andador sólo depende de la posición en la que se encuentre, y no de ningún escalón precedente. Cuando el sistema no tiene memoria de dónde estaba antes, lo llamamos sistema markoviano.
• En términos generales, hay muchos sabores de un problema estocástico en el que se describe la probabilidad de estar en una posición\(x\) a la vez\(t\), y estos se pueden categorizar por si\(x\) y\(t\) son tratados como variables continuas o discretas. La clase de problema que estamos discutiendo con discretos\(x\) y\(t\) puntos se conoce como una Cadena Markov. El caso donde el espacio se trata discretamente y el tiempo continuamente da como resultado una Ecuación Maestra, mientras que una ecuación de Langevin o ecuación de Fokker—Planck describe el caso de continuo\(x\) y\(t\).
• Para describir la dependencia del tiempo de los caminantes, relacionamos la distribución de probabilidad en un punto en el tiempo\(P(x,t+Δt)\), con la distribución de probabilidad para el paso de tiempo anterior,\(P(x,t)\) en términos de las probabilidades de que un caminante haga un paso a la derecha (\(P_+\)) o a la izquierda (\(P_-\)) durante el intervalo\(Δt\). Tenga en cuenta\(P_+\neq P_-\), cuando, hay un sesgo de paso en el sistema. Si\(P_+ + P_-<1\), hay una resistencia a pisar ya sea como resultado de una barrera energética o volumen excluido en la cadena.
• Además de la pérdida de probabilidad al alejarse de x a la izquierda o derecha, necesitamos dar cuenta de los pasos de sitios adyacentes que terminan en\(x\).

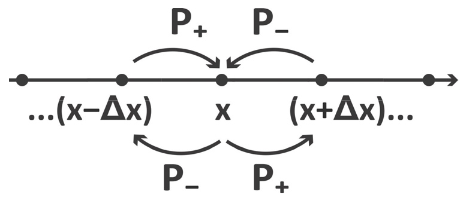
Entonces la probabilidad de observar la partícula en posición\(x\) durante el intervalo\(Δ\) t es:

\[\begin{aligned} P(x,t+\Delta t) &= P(x,t)-P_+\cdot P(x,t) -P_- \cdot P(x,t) +P_+\cdot P(x-\Delta x,t)+P_- \cdot P(x+\Delta x,t) \\[4pt] &= (1-P_+-P_-) \cdot P(x,t)+P_+ \cdot P(x-\Delta x,t) +P_- \cdot P(x+\Delta x,t) \\[4pt] &= P(x,t) + P_+[P(x-\Delta x,t)-P(x,t)]+ P_-[P(x+\Delta x,t)-P(x,t)] \end{aligned} \]

y la probabilidad de cambio neto es

\[ P(x,t+\Delta t) - P(x,t) = P_+[P(x-\Delta x,t) - P(x,t)]+P_-[P(x+\Delta x,t)-P(x,t)] \nonumber \]

Podemos lanzar esto como una derivada del tiempo si dividimos el cambio de probabilidad por el paso de tiempo Δt:

\[ \begin{aligned} \dfrac{\partial P}{\partial t} &= \dfrac{P(x,t+\Delta t)-P(x,t)}{\Delta t} \\[4pt] &= P_+[P(x-\Delta x,t) - P(x,t)]+P_-[P(x+\Delta x,t)-P(x,t)] \\[4pt] &= P_+ \Delta P_-(x,t)+P_-\Delta P_+(x,t) \end{aligned} \]\[\]

¿Dónde\(P_{\pm} = P_{\pm} / \Delta t\) está la velocidad de escalonamiento derecha e izquierda, y\( \Delta P_{\pm}(x,t) = P(x \pm \Delta x,t)-P(x,t) \)

Nos gustaría mostrar que este modelo de caminata aleatoria da como resultado una ecuación de difusión para la densidad de probabilidad ρ (x, t) que deducimos en la Ecuación (11.1.5). Para simplificar, suponemos que las probabilidades de paso a la izquierda y derecha\(P_+=P_-=\frac{1}{2}\), y sustituyen

\[ P(x,t) = \rho (x,t) dx \nonumber \]

en la Ecuación (11.2.1):

\[ \dfrac{\partial \rho}{\partial t} = P[\rho(x-\Delta x,t)-2 \rho (x,t)+\rho (x+\Delta x,t)] \nonumber \]

donde\(P=1/2 \, \Delta t \). Luego expandimos estos términos de densidad de probabilidad en x como

\[ \rho (x,t) = \rho (0,t) + \dfrac{\partial \rho}{\partial x} x+\dfrac{1}{2} \dfrac{\partial^2 \rho}{\partial x^2} x^2 \nonumber \]

y encontrar que la densidad de probabilidad sigue una ecuación de difusión

\[ \dfrac{\partial \rho}{\partial t} = D \dfrac{\partial^2 \rho}{\partial x^2} \nonumber \]

donde\(D= \Delta x^2/2 \Delta t\).

___________________________________

Materiales de lectura

• A. Nitzan, Dinámica Química en Fases Condensadas: Relajación, Transferencia y Reacciones en Sistemas Molecular Condensados. (Oxford University Press, Nueva York, 2006).