3.4: Bomba-Sonda

El experimento bomba-sonda o absorción transitoria es quizás el experimento no lineal de tercer orden más utilizado. Se puede utilizar para seguir muchos tipos de procesos de relajación dependientes del tiempo y dinámicas químicas, y se usa más comúnmente para seguir la relajación poblacional, cinética química o dinámica de wavepacket y ritmos cuánticos.

El principio es bastante simple, y el uso del formalismo teórico de la espectroscopia no lineal a menudo es innecesario para interpretar el experimento. Dos pulsos separados por un retardo\(\tau\) se cruzan en una muestra: un pulso de bomba y un pulso de sonda retardado en el tiempo. El pulso de la bomba\(E_{pu}\) crea un estado de no equilibrio, y los cambios dependientes del tiempo en la muestra se caracterizan por el pulso de sonda\(E_{pr}\) a través del cambio de intensidad inducido por la bomba en la sonda transmitida,\(\Delta I\).

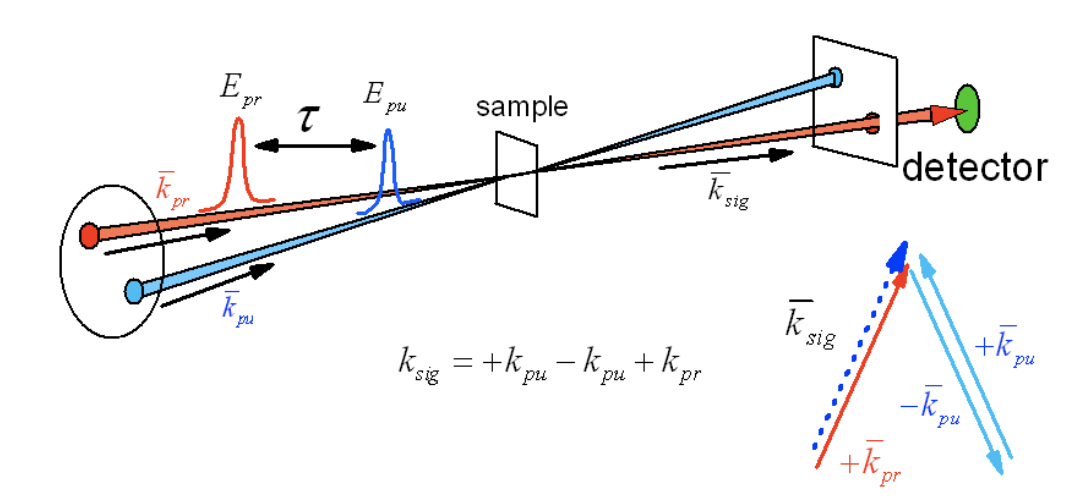
Descrita como una espectroscopía no lineal coherente de tercer orden, la señal se irradia colineal al campo de sonda transmitido, por lo que la condición de coincidencia del evector de ondas es

\[\bar k_{sig}=+\bar k_{pu} -\bar k_{pu} +\bar k_{pr}=\bar k_{pr}.\]

Hay dos interacciones con el campo de bombeo y la tercera interacción es con la sonda. Similar a la rejilla transitoria, no se puede distinguir el orden de tiempo de las interacciones de bomba, por lo que los términos que contribuyen a la dispersión a lo largo de la sonda son\(k_{sig}=\pm k_1 \mp k_2 + k_3\) (es decir, todas las funciones de correlación _R1 a _R4). De hecho, la bomba-sonda se puede considerar como el límite del experimento de rejilla transitoria en el límite del vector de onda de rejilla cero (\(\theta\)y\(\beta\rightarrow 0\)).

El detector observa la intensidad de la sonda transmitida y la señal no lineal

\[I=\frac{nc}{4\pi}|E_{pr}'+E_{sig}|^2 \label{4.4.1}\]

\(E_{pr}'\)es el campo de sonda transmitido corregido para la propagación lineal a través de la muestra. La señal medida es típicamente la intensidad diferencial en el campo de la sonda con y sin el campo de bombeo presente:

\[\Delta I(\tau)=\frac{nc}{4\pi}\left\{|E_{pr}'+E_{sig}(\tau)|^2-|E_{pr}'|^2\right\} \label{4.4.2}\]

Si trabajamos bajo condiciones de una señal débil en relación con la sonda transmitida\(|E_{pr}'|\gt\gt|E_{sig}|\), entonces la intensidad diferencial en eq. (4.4.2) está dominada por el término cruzado

\[\begin{aligned} \Delta I(\tau) & \approx \frac{n c}{4 \pi}\left[E_{p r}^{\prime} E_{s i g}^{*}(\tau)+c . c .\right] \\ &=\frac{n c}{2 \pi} \operatorname{Re}\left[E_{p r}^{\prime} E_{s i g}^{*}(\tau)\right] \end{aligned}\label{4.4.3}\]

Entonces la señal bomba-sonda es directamente proporcional a la respuesta no lineal. Dado que el campo de señal está relacionado con la polarización no lineal a través de un desplazamiento de fase\ (\ pi/2),

\[\bar E_{sig}(\tau)=i\frac{2\pi\omega_{sig}\ell}{nc}P^{(3)}(\tau)\label{4.4.4}\]

la señal medida de la bomba-sonda es proporcional a la parte imaginaria de la polarización

\[\Delta I(\tau)=2\omega_{sig}\ell Im\left[E_{pr}'P^{(3)}(\tau)\right]\label{4.4.5}\]

que también es proporcional a las funciones de correlación derivadas de los diagramas resonantes que consideramos anteriormente.

Respuesta Dicroica y Birrefringente

En analogía a lo que observamos anteriormente para la espectroscopia lineal, los cambios no lineales en la absorción del campo sondeo transmitido están relacionados con la parte imaginaria de la susceptibilidad, o la parte imaginaria del índice de refracción. Además de los procesos totalmente resonantes, también es posible que el campo de bombeo induzca cambios no resonantes en la polarización que modulen la parte real del índice de refracción. Estas pueden describirse a través de una variedad de interacciones no resonantes, como Raman no resonante, el efecto Kerr óptico, la dispersión coherente de Raleigh o Brillouin, o la segunda hiperpolarizabilidad de la muestra. En este caso, podemos describir el desarrollo temporal del campo de polarización y señal radiada como

\[\begin{aligned} P^{(3)}(\tau,\tau_3) &= P^{(3)}(\tau,\tau_3)e^{-i\omega_{sig}\tau_3}+\left[P^{(3)}(\tau,\tau_3)\right]^*e^{i\omega_{sig}}\tau_3 \\ &= 2Re\left[P^{(3)}(\tau,\tau_3)\right]\cos{(\omega_{sig}\tau_3)}+2Im\left[P^{(3)}(\tau,\tau_3)\right]\sin{(\omega_{sig}\tau_3)} \end{aligned}\label{4.4.6}\]

\[\begin{aligned}\bar E_{sig}(\tau_3) &=\frac{4\pi\omega_{sig}\ell}{nc}\left(Re\left[P^{(3)}(\tau,\tau_3)\right]\sin{(\omega_{sig}\tau_3)}+Im\left[P^{(3)}(\tau,\tau_3)\right]\cos{(\omega_{sig}\tau_3)}\right) \\ &= E_{bir}(\tau,\tau_3)\sin{(\omega_{sig}\tau_3)}+E_{dic}(\tau,\tau_3)\cos{(\omega_{sig}\tau_3)} \end{aligned}\label{4.4.7}\]

Aquí la señal se expresa como una suma de dos contribuciones, referidas como las\((E_{dic})\) respuestas birrefringentes\((E_{bir})\) y dicroicas. Como antes la parte imaginaria, o respuesta dicroica, describe la variación de amplitud inducida por muestra en el campo de señal, mientras que la respuesta birrefringente corresponde a la parte real de la polarización no lineal y representa el desplazamiento de fase o retardo del campo de señal inducido por la muestra.

En este esquema, la sonda transmitida es

\[\bar E_{pr}'(\tau_3)=E_{pr}'(\tau_3)\cos{(\omega_{pr}\tau_3)} \label{4.4.8}\]

Para que el

\[\Delta I(\tau)\approx\frac{nc}{2\pi}\left[E_{pr}'(\tau)E_{dic}(\tau)\right] \label{4.4.9}\]

Debido a que la señal está en cuadratura con la polarización (desplazamiento de\(\pi/2\) fase), la respuesta absortiva o dicroica está en fase con la sonda transmitida, mientras que no se observa la parte birrefringente. Si permitimos que se controle la fase del campo de la sonda, por ejemplo a través de una placa de cuarto de onda antes de la muestra, entonces podemos escribir

\[\bar E_{pr}'(\tau_3,\phi)=E_{pr}'(\tau_3)\cos{(\omega_{pr}\tau_3+\phi)} \label{4.4.10}\]

\[I(\tau,\phi)\approx\frac{nc}{2\pi}\left[E_{pr}'(\tau)E_{bir}(\tau)\sin{(\phi)}+E_{pr}'(\tau)E_{dic}(\tau)\cos{(\phi)}\right] \label{4.4.11}\]

La respuesta birrefringente y dicroica del sistema molecular ahora se puede observar para las fases de\(\phi=\pi/2,3\pi/2\dots\) y\(\phi=0,\pi\dots\), respectivamente.

Experimentos incoherentes de bomba-sonda

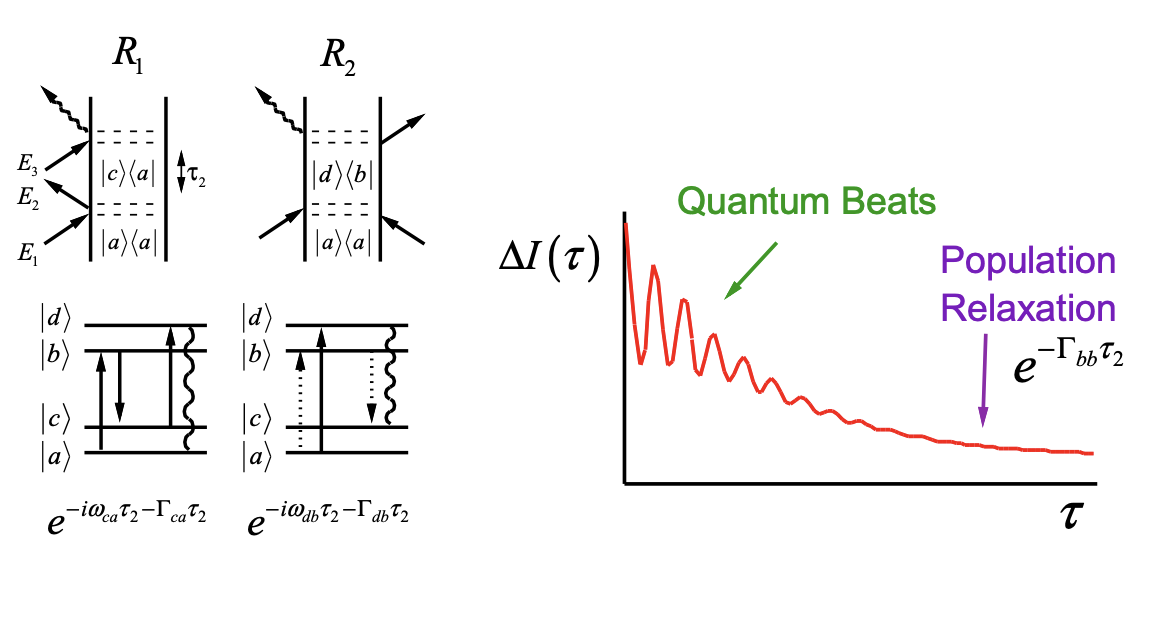
¿Qué información contiene el experimento bomba-sonda? Dado que el retardo de tiempo que controlamos es el segundo intervalo de tiempo\(\tau_2\), los diagramas para un sistema de dos niveles indican que estos miden la relajación poblacional:

\[\Delta I(\tau)\propto|\mu_{ab}|^4e^{-\Gamma_{bb}\tau} \label{4.4.12}\]

De hecho, medir los cambios poblacionales y la relajación son el uso más común de este experimento. Cuando la desfase es muy rápida, la bomba-sonda puede interpretarse como un experimento incoherente, y el cambio de intensidad diferencial (o absorción) es proporcional al cambio de población de los estados observados por el campo de la sonda. Los cambios de población inducidos por la bomba en los estados de la sonda se pueden describir mediante ecuaciones de velocidad que describen la relajación poblacional, la redistribución o la cinética química. Para el caso donde las frecuencias de bomba y sonda son las mismas, la señal decae como resultado de la relajación poblacional del estado inicialmente excitado. Los diagramas del sistema de dos niveles indican que la evolución en\(\tau_2\) se diferencia por la evolución en el suelo o estado excitado. Estos diagramas reflejan las contribuciones de señal iguales del blanqueador del estado fundamental (pérdida de la población del estado fundamental) y la emisión estimulada del estado excitado. Para la relajación directa de estado excitado a suelo la pérdida de población en el estado excitado\(\Gamma_{bb}\) es lo mismo que la recarga del agujero en el estado suelo\(\Gamma_{aa}\), de manera que eso\(\Gamma_{aa}=\Gamma_{bb}\). Si la relajación de la población desde el estado excitado es a través de un intermedio, entonces el decaimiento bomba-sonda reflejará contribuciones iguales de ambos procesos, lo que puede describirse mediante ecuaciones de tasa de primer orden acopladas.

Cuando las frecuencias de resonancia de los campos de bomba y sonda son diferentes, entonces la señal incoherente bomba-sonda se relaciona con la probabilidad conjunta de excitar el sistema en\(\omega_{pu}\) y detectar en\(\omega_{pr}\) después de esperar un tiempo\(\tau\),\(P(\omega_{pr},\tau;\omega_{pu})\).

Experimentos coherentes de bomba-sonda

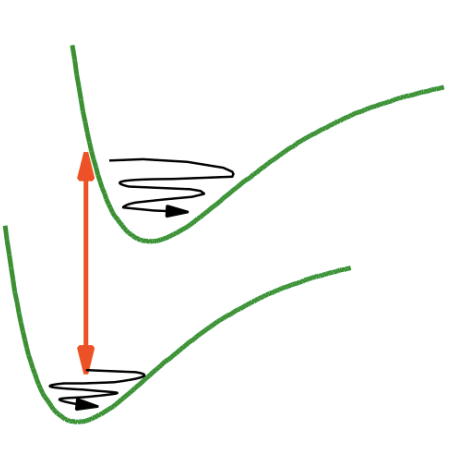
Las mediciones ultrarrápidas de bomba-sonda en la escala de tiempo de desfase vibracional operan en un régimen coherente donde las ondas preparadas por el pulso de bomba modulan la intensidad de la sonda. Esto proporciona un mecanismo para estudiar la dinámica de estados electrónicos excitados con vibraciones acopladas y dinámicas de reacciones químicas fotoiniciadas. Si consideramos el caso de experimentos bomba-sonda en estados electrónicos donde\(\omega_{pu}=\omega_{pr}\), nuestra descripción de la bomba-sonda a partir de diagramas de Feynmann indica que el pulso de bomba crea excitaciones tanto en el estado excitado como en el estado fundamental. Ambos wavepackets contribuirán a la señal.

Existen dos formas equivalentes de describir el experimento, que reflejan nuestra descripción anterior de la espectroscopia electrónica para una transición electrónica acoplada al movimiento nuclear. El primero es describir la espectroscopia en términos de los autoestados de\(H_0, |e,n\rangle\). El segundo se basa en la brecha energética hamiltoniana para describir la espectroscopia como dos niveles electrónicos\(H_S\) que interactúan con los grados vibracionales de libertad\(H_B\), y la dinámica de wavepacket son capturados por\(H_{SB}\).

Para la descripción del estado propio, un sistema de dos niveles es inadecuado para capturar la dinámica de wavepacket. En su lugar, describa la espectroscopia en términos de los diagramas de sistema de cuatro niveles dados anteriormente. Además de los términos de relajación poblacional, vemos que los términos _R2 y R ₄ describen la evolución de las coherencias en el estado electrónico excitado, mientras que los términos _R1 y R ₃ describen el paquete de ondas del estado fundamental. Para un conjunto de ondas subamortiguado, estas coherencias se observan como latidos cuánticos en la señal bomba-sonda.