6.1: Grados de libertad espacial, coordenadas normales y modos normales

Para hacer frente a la complejidad del movimiento vibratorio en moléculas poliatómicas, necesitamos utilizar los tres conceptos importantes enumerados como título de esta sección. Por un grado de libertad espacial, nos referimos a una dirección de movimiento independiente. Un solo átomo tiene tres grados espaciales de libertad porque puede moverse en tres direcciones independientes u ortogonales en el espacio, es decir, a lo largo de los ejes x, y o z de un sistema de coordenadas cartesianas. El movimiento en cualquier otra dirección resulta de combinar componentes de velocidad a lo largo de dos o tres de estas direcciones. Dos átomos tienen seis grados espaciales de libertad porque cada átomo puede moverse en cualquiera de estas tres direcciones independientemente.

Equivalentemente, también podemos decir que un átomo tiene tres grados espaciales de libertad porque necesitamos especificar los valores de tres coordenadas\((x_1, y_1, z_1)\) para localizar el átomo. Dos átomos tienen seis grados espaciales de libertad porque necesitamos especificar los valores de seis coordenadas,\((x_1, y_1, z_1)\) y\((x_2, y_2, z_2)\), ubicar dos átomos en el espacio. En general, para ubicar los átomos de N en el espacio, necesitamos especificar coordenadas 3N, por lo que una molécula compuesta por átomos de N tiene 3N grados espaciales de libertad.

Ejercicio\(\PageIndex{1}\)

Identificar el número de grados espaciales de libertad para las siguientes moléculas:\(Cl_2\),\(CO_2\),\(H_2O\),\(CH_4\),\(C_2H_2\),\(C_2H_4\),\(C_6H_6\).

El movimiento de los núcleos atómicos en una molécula no es tan simple como traducir cada uno de los núcleos independientemente a lo largo de los ejes x, y y z porque los núcleos, que están cargados positivamente, están acoplados entre sí por las interacciones electrostáticas con los electrones, los cuales están cargados negativamente. Los electrones entre dos núcleos los atraen efectivamente entre sí, formando un enlace químico.

Consideremos el caso de una molécula diatómica, que tiene seis grados de libertad. El movimiento de los átomos está limitado por el enlace. Si un átomo se mueve, se ejercerá una fuerza sobre el otro átomo debido al vínculo. La situación es como dos bolas acopladas entre sí por un resorte. Todavía hay seis grados de libertad, pero el movimiento del átomo 1 a lo largo de x, y, y z no es independiente del movimiento del átomo 2 a lo largo de x, y, y z porque los átomos están unidos entre sí.

Por lo tanto, no es muy útil usar las seis coordenadas cartesianas,\((x_1, y_1, z_1)\) y\((x_2, y_2, z_2)\), describir los seis grados de libertad porque los dos átomos están acoplados entre sí. Necesitamos nuevas coordenadas que sean independientes entre sí y que, sin embargo, den cuenta del movimiento acoplado de los dos átomos. Estas nuevas coordenadas se denominan coordenadas normales, y el movimiento descrito por una coordenada normal se denomina modo normal.

Una coordenada normal es una combinación lineal de coordenadas de desplazamiento cartesiano. Una combinación lineal es una suma de términos con coeficientes de ponderación constantes multiplicando cada término. Los coeficientes pueden ser imaginarios o cualquier número positivo o negativo incluyendo +1 y -1. Por ejemplo, el punto o vector r = (1, 2, 3) en el espacio tridimensional se puede escribir como una combinación lineal de vectores unitarios.

\[r = 1 \bar {x} + 2 \bar {y} + 3 \bar {z} \label {6-1}\]

Una coordenada de desplazamiento cartesiano da el desplazamiento en una dirección particular de un átomo desde su posición de equilibrio. Las posiciones de equilibrio de todos los átomos son aquellos puntos donde ninguna fuerza está actuando sobre ninguno de los átomos. Por lo general, los desplazamientos desde el equilibrio se consideran pequeños. Para ilustración, las coordenadas de desplazamiento cartesiano para HCl se definen en la Tabla\(\PageIndex{1}\), y se ilustran en la Figura\(\PageIndex{1}\).

Cuadro 6. Coordenadas de desplazamiento cartesiano para HCl. *

\[q_1 = X_{H} - X^e_H\]

\[q_2 = y_{H} - y^e_H\]

\[q_3 = z_H - z^e_H\]

\[q_4 = x_{Cl} - x^e_{Cl}\]

\[q_5 = y_{Cl} - y^e_{Cl}\]

\[q_6 = z_{Cl} - z^e_{Cl}\]

*El superíndice e designa el valor de la coordenada en la posición de equilibrio.

Tenga en cuenta que la posición de un átomo puede escribirse como un vector\(r_1\) donde\(r_1 = (x_1, y_1, z_1)\), y las posiciones de dos átomos se pueden escribir como dos vectores\(r_1\) y\(r_2\) o como un vector generalizado que contiene los seis componentes\(r = (x_1, y_1, z_1, x_2, y_2, z_2)\). De manera similar, las seis coordenadas de desplazamiento cartesiano pueden escribirse como un vector generalizado de este tipo\(q = (q_1, q_2, q_3, q_4, q_5, q_6)\).

Figura\(\PageIndex{1}\): Las coordenadas de desplazamiento cartesiano para HCl. Tenga en cuenta que el eje internuclear es el eje x.

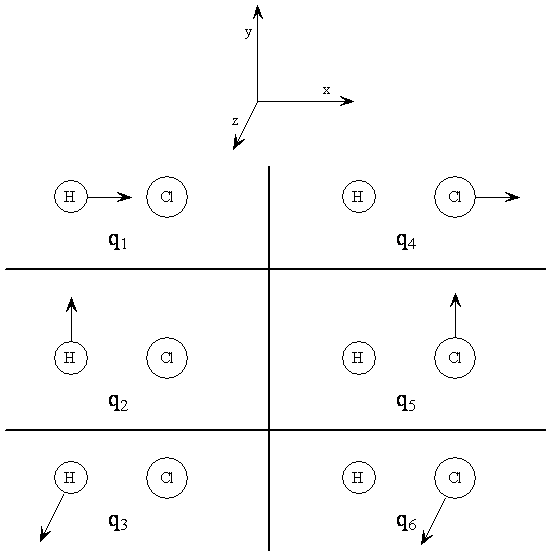
Para una molécula diatómica es fácil encontrar las combinaciones lineales de las coordenadas de desplazamiento cartesiano que forman las coordenadas normales y describen los modos normales. Basta con tomar sumas y diferencias de las coordenadas de desplazamiento cartesiano. Consulte Tabla\(\PageIndex{1}\) y Figura\(\PageIndex{4}\). para la definición de las q's. La combinación q1 + q4 corresponde a la traducción de toda la molécula en la dirección x; llamar a esta coordenada normal Tx. De igual manera podemos definir Ty = q2 + q5 y Tz = q3 + q6 como traducciones en las direcciones y y z, respectivamente. Ahora tenemos tres coordenadas normales que dan cuenta de tres de los grados de libertad, las tres traducciones de toda la molécula.

¿Qué hacemos con los tres grados de libertad restantes? Aquí usemos una regla simple para hacer ciencia creativa: si una cosa funciona, prueba algo similar y examina el resultado. En este caso, si sumar cantidades funciona, intente restarlas. Examine la combinación q2 - q5. Esta combinación significa que H se desplaza en una dirección y Cl se desplaza en la dirección opuesta. Debido al enlace, los dos átomos no pueden alejarse completamente, por lo que este pequeño desplazamiento de cada átomo desde el equilibrio es el comienzo de una rotación alrededor del eje z. Llama a esta coordenada normal Rz. De manera similar definir Ry = q3 - q6 para que sea rotación alrededor del eje y. Ahora hemos encontrado dos coordenadas normales rotacionales correspondientes a dos grados de libertad rotacional.

La combinación restante, q1 - q4, corresponde a los átomos que se mueven uno hacia el otro a lo largo del eje x. Este movimiento es el comienzo de una vibración, es decir, la oscilación de los átomos hacia adelante y hacia atrás a lo largo del eje x alrededor de sus posiciones de equilibrio, y representa el sexto grado de libertad restante. Utilizamos Q para la coordenada normal vibracional.

\[Q = q_1 - q_4 \label {6-2}\]

Para resumir: una coordenada normal es una combinación lineal de coordenadas de desplazamiento cartesiano atómico que describe el movimiento acoplado de todos los átomos que comprenden una molécula. Un modo normal es el movimiento acoplado de todos los átomos descritos por una coordenada normal. Mientras que las moléculas diatómicas tienen solo un modo vibracional normal y por lo tanto una coordenada vibracional normal, las moléculas poliatómicas tienen muchas.

Ejercicio\(\PageIndex{2}\)

Dibuje y etiquete seis diagramas, cada uno similar a la Figura\(\PageIndex{1}\), para mostrar las 3 coordenadas traslacionales, 2 rotacionales y 1 vibracional normales de una molécula diatómica.

Ejercicio\(\PageIndex{3}\)

Los modos vibracionales normales tienen varias características distintivas. Examinar las animaciones para los modos normales de benceno mostrados i n Figura\(\PageIndex{3}\) to identificar y hacer una lista de estas características. Utilice un programa de modelado molecular para calcular y visualizar los modos normales de otra molécula.

La lista de características distintivas de los modos normales que compiló en Ejercicio\(\PageIndex{4}\) debe incluir las siguientes cuatro propiedades. De no ser así, reexaminar las animaciones para confirmar que estas características están presentes.

1. En un modo normal vibracional particular, los átomos se mueven alrededor de sus posiciones de equilibrio de manera sinusoidal con la misma frecuencia.
2. Cada átomo alcanza su posición de desplazamiento máximo al mismo tiempo, pero la dirección del desplazamiento puede diferir para diferentes átomos.
3. Aunque los átomos se mueven, las relaciones entre las posiciones relativas de los diferentes átomos no cambian.
4. El centro de masa de la molécula no se mueve.

Para el ejemplo de HCl, ver Tabla\(\PageIndex{1}\), la primera propiedad, expresada matemáticamente, significa

\[q_1 = A_1 \sin (\omega t) \text {and} q_4 = A_4 \sin (\omega t) \label {6-3}\]

Los desplazamientos o amplitudes máximos están dados por A1 y A4, y la frecuencia de oscilación (en radianes por segundo) es ω para ambas coordenadas de desplazamiento involucradas en el modo vibratorio normal de HCl. Sustitución de Ecuaciones (6-3) por las coordenadas de desplazamiento en la expresión determinada anteriormente para la coordenada normal vibracional, Ecuación (6-2), rinde

\[ Q = q_1 - q_4 = A_1 \sin (\omega t) - A_4 \sin (\omega t) \label {6-4}\]

Esta expresión dependiente del tiempo describe los movimientos acoplados de los átomos de hidrógeno y cloro en una vibración de la molécula de HCl. En general para una molécula poliatómica, la magnitud del desplazamiento de cada átomo en un modo vibracional normal puede ser diferente, y algunos pueden ser cero. Si una amplitud, la A, para algún átomo en alguna dirección es cero, significa que el átomo no se mueve en esa dirección en ese modo normal. En diferentes modos normales, los desplazamientos de los átomos son diferentes, y las frecuencias del movimiento generalmente son diferentes. Si dos o más modos vibracionales tienen la misma frecuencia vibracional, estos modos se denominan degenerados.

Probablemente notaste en Ejercicio\(\PageIndex{4}\) que los átomos alcanzaron puntos extremos en su movimiento al mismo tiempo pero que no todos se movían en la misma dirección al mismo tiempo. Estas características son descritas por la segunda y tercera propiedades de la lista anterior. Para el caso del HCl, los dos átomos siempre se mueven en direcciones exactamente opuestas durante la vibración. Matemáticamente, el signo negativo en la Ecuación que desarrollamos para la coordenada normal, Q, da cuenta de esta relación.

Esta sincronización con respecto a la dirección del movimiento se llama la fase de los átomos. En un modo normal, los átomos se mueven con una relación de fase constante entre sí. La relación de fase está representada por un ángulo de fase φ en el argumento de la función sinusoidal que describe la oscilación de tiempo, sin (ωt + φ). El ángulo se llama ángulo de fase porque desplaza la función sinusoidal en el eje de tiempo. Podemos ilustrar esta relación de fase para HCl. Utilizar la identidad trigonométrica

\[- \sin {\theta} = \sin (\theta + 180^0) \label {6-5}\]

en Ecuación\ ref {6-4} para obtener

\[Q = A_1 \sin (\omega t ) + A_4 \sin (\omega t + 180^0) \label {6-6}\]

para ver que el ángulo de fase para este caso es de 180 ^o.

El ángulo de fase\(\varphi\) explica que el átomo de H y el átomo de Cl alcanzan sus desplazamientos máximos en la dirección x positiva, +A1 y +A4, en diferentes momentos. Generalmente en un modo normal el ángulo de fase\(\varphi\) es 0o o 180o. Si\(\varphi\) = 0o para ambos átomos, los átomos se mueven juntos, y se dice que están en fase. Para la vibración de una molécula diatómica como HCl, el ángulo de fase para un átomo es\(\varphi\) = 0o, y el ángulo de fase para el otro átomo es\(\varphi\) = 180o. Por lo tanto, los átomos se mueven en direcciones opuestas en cualquier momento, y se dice que los átomos están 180o fuera de fase. Cuando\(\varphi\) es 180o, dos átomos alcanzan los puntos extremos en su movimiento al mismo tiempo, pero uno está en la dirección positiva y el otro en la dirección negativa.

Las relaciones de fase se pueden ver viendo una banda de música. Todos los jugadores están ejecutando el mismo movimiento de marcha con la misma frecuencia, pero algunos pueden estar por delante o por detrás del resto. Se podría decir: “Están desfasados”. También se podría decir: “Están desfasados. “

Para ilustrar la cuarta propiedad del HCl, recuerde que el centro de masa de una molécula diatómica se define como el punto donde se satisface la siguiente ecuación.

\[m_H d_H = m_{Cl} d_{Cl} \label {6-7}\]

Las masas de los átomos están dadas por\(m_H\) y\(m_Cl\),\(d_H\) y\(d_{Cl}\) son las distancias de estos átomos desde el centro de masa.

Ejercicio\(\PageIndex{4}\)

Encuentra las distancias, dH y DCl, de los átomos de H y Cl desde el centro de masa en HCl dado que la longitud del enlace es de 0.13 nm. En general para una molécula diatómica, AB, ¿qué determina la relación Da/dB, y qué átomo se mueve la mayor distancia en la vibración?

En general, para satisfacer la condición del centro de masa, un átomo de luz se localiza más lejos del centro de masa que un átomo pesado. Para mantener el centro de masa fijo durante una vibración, la amplitud de movimiento de un átomo debe depender inversamente de su masa. En otras palabras, un átomo de luz se localiza más lejos del centro de masa y se mueve una distancia más larga en una vibración que un átomo pesado.

Ejercicio\(\PageIndex{5}\)

Encuentre la relación de A1 a A4 de Equ ación que mantenga el centro de masa de HCl estacionario durante una vibración. Encuentra valores para A1 y A4 que satisfagan la condición

\[A12 + A42= 1.\]

Ejercicio\(\PageIndex{6}\)

Para una molécula de HCl vibrante, utilice las cuatro propiedades de un modo vibratorio normal, enumeradas anteriormente, para esbozar una gráfica que muestre la posición del átomo de H (gráfico 1) y la posición del átomo de Cl (gráfico 2) en función del tiempo. Ambas parcelas deben estar en la misma escala. Pista: coloca x en el eje vertical y el tiempo en el eje horizontal.

En general, una molécula con 3N grados de libertad espacial tiene 3 modos normales de traducción (a lo largo de cada uno de los tres ejes), 3 modos normales rotacionales (alrededor de cada uno de los tres ejes) y 3N-6 (el número restante) diferentes modos de movimiento normales vibracionales. Una molécula lineal, como acabamos de ver, solo tiene dos modos rotacionales, por lo que hay modos normales vibracionales 3N-5. El movimiento rotacional alrededor del eje internuclear en una molécula lineal no es uno de los 3N grados espaciales de libertad derivados de la traducción de átomos en el espacio tridimensional. Más bien, dicho movimiento corresponde a otros grados de libertad, movimiento rotacional de los electrones y un movimiento giratorio de los núcleos. De hecho, la función de onda electrónica para una molécula lineal se caracteriza por algún momento angular (rotación) alrededor de este eje, y los núcleos tienen una propiedad llamada espín.

Ejercicio\(\PageIndex{7}\)

Identificar el número de modos normales traslacionales, rotacionales y vibracionales para las siguientes moléculas:\(Cl_2, CO_2, H_2O, CH_4, C_2H_2, C_2H_4, C_2H_6, C_6H_6\). Usando tu intuición, dibuja diagramas similares a los del Ejercicio\(\PageIndex{3}\) para mostrar los modos normales de\(H_2O\) y\(C_2H_4\). Es difícil identificar los modos normales de moléculas triatómicas y de mayor tamaño por intuición. Un análisis matemático es esencial. Es más fácil ver los modos normales si usas un programa de modelado molecular como Espartano o Gaussiano para generar y mostrar los modos normales.

Probablemente encontraste al intentar completar Ejercicio\(\PageIndex{7}\) que es difícil identificar los modos normales y las coordenadas normales de moléculas triatómicas y grandes por intuición. Un análisis matemático es esencial. Se describe por separado un análisis general basado en la formulación lagrangiana de la mecánica clásica.