7.5: Propiedades mecánicas cuánticas de moléculas diatómicas giratorias
- Page ID
- 71225
En esta sección examinamos los estados rotacionales de una molécula diatómica comparando la interpretación clásica del vector de momento angular con la interpretación probabilística de las funciones de onda de momento angular. Queremos responder a los siguientes tipos de preguntas. ¿Cómo se describe la orientación de una molécula diatómica giratoria en el espacio? ¿La molécula está rotando realmente? ¿Qué propiedades de la molécula se pueden observar físicamente? ¿De qué manera difiere la descripción mecánica cuántica de una molécula giratoria de la imagen clásica de una molécula giratoria?
Introducción
En el espacio isotrópico, es decir, todas las direcciones son equivalentes, cualquier molécula dada puede tener cualquier orientación. El eje z puede tener cualquier orientación. Dado que no podemos distinguir diferentes direcciones en el espacio isotrópico, diferentes moléculas tendrán diferentes vectores de momento angular y todas las orientaciones de estos vectores en el espacio serán igualmente probables. Así por ejemplo, a pesar de que nuestra descripción mecánica cuántica dice que solo se permiten tres estados con diferentes orientaciones de momento angular y ejes internucleares para el nivel de\(J = 1\) energía (\(m_J = 0, 1, -1\)), no hay consecuencias prácticas de este hecho en el espacio isotrópico.
Podemos hacer que el espacio sea anisotrópico aplicando un campo externo, por ejemplo, un campo eléctrico o un campo magnético. La dirección del campo es una dirección única en el espacio, y es más conveniente asignar el eje z a esa dirección. Nuestras funciones de onda rotacionales y operadores implícitamente están diseñados para que z sea el eje especial debido a las relaciones entre las coordenadas esféricas y las coordenadas cartesianas. Los efectos de los campos eléctricos y magnéticos externos sobre los espectros atómicos y moleculares es un área activa de investigación que ha proporcionado mucha información sobre las propiedades de los átomos y moléculas y el uso de la mecánica cuántica para describirlas. Por ejemplo, los efectos del campo magnético sobre los espectros atómicos contribuyeron al descubrimiento del espín electrónico y se discuten en el siguiente capítulo. Estos efectos se conocen como efectos Stark (campo eléctrico) y efectos Zeeman (campo magnético) después de los pioneros que los descubrieron.
Para el estado fundamental, J = 0, la energía rotacional y el momento angular son cero. ¡Sin energía rotacional o momento angular, la molécula no puede estar rotando! Puede estar vibrando y traduciendo, pero no está rotando. ¿Cuál es su orientación en el espacio? Examine la función de onda en la Figura\(\PageIndex{9}\). Todos los valores de\(\theta\) y\(\varphi\) son igualmente probables; no tenemos información sobre la orientación de la molécula en este estado. El hecho de que no haya incertidumbre en el momento angular (es exactamente cero), y no hay información sobre la orientación (la incertidumbre es infinita) es consistente con el Principio de Incertidumbre de Heisenberg.
El espacio para un rotor rígido está definido por todos los valores para las variables\(\theta\) y\(\varphi\). Dado que un rotor rígido no está limitado a ninguna región de este espacio por un límite potencial, la energía y el momento angular pueden ser cero porque la incertidumbre en la ubicación del rotor en este espacio es infinita. El rotor puede estar en cualquier lugar;\(\theta\) y\(\varphi\) puede tener cualquier valor. Esta situación es análoga a la partícula libre, donde conocíamos exactamente el impulso pero no teníamos conocimiento de la posición de la partícula. Cuando\(J\) es diferente de 0, la incertidumbre en la ubicación del rotor disminuye. Es más probable que se encuentre en algunas regiones del espacio que en otras. Esta disminución de la incertidumbre sobre la ubicación del rotor va acompañada de un aumento en la incertidumbre en el momento angular como lo requiere el Principio de Incertidumbre. Aún conocemos exactamente la magnitud del vector de momento angular, pero su dirección en el espacio es incierta.
A continuación considere el caso\(J = l\) con\(m_J = +1, 0, -1\). La longitud de los vectores de momento angular para todos estos estados es\(\sqrt {2} \hbar\), ver Ejercicio\(\PageIndex{16}\) y Figura\(\PageIndex{11}\). Desde una perspectiva clásica, el valor distinto de cero para el momento angular significa que la molécula debe estar rotando. Las proyecciones de los vectores sobre el eje z son, 0 y -para los\(m_J = +1, 0, -1\) estados, respectivamente. La interpretación clásica de este resultado es que, si bien el plano de rotación de la molécula, que es perpendicular al vector de momento angular que describe cada estado, está confinado a una orientación específica con respecto al eje z, no se limita con respecto a los ejes x e y.
El cuadro clásico de rotación e interpretación del vector de momento angular para el\(m_J = 0\) estado J = 1, coloca el eje internuclear en las posiciones mostradas en la Figura\(\PageIndex{1}\), rotando con igual probabilidad en cualquier plano que contenga el eje z pero sin restricciones con respecto al ángulo\(\varphi\) .

Para el\(J = 1\),\(m_J = 1\) y\(m_J = -1\) estados, las funciones de onda están dadas por
\[ \begin{align} Y^1_1 &= \sqrt {\frac {3}{8 \pi}} \sin \theta e^{i \varphi} \\[4pt] Y^{-1}_1 &= \sqrt {\frac {3}{8 \pi}} \sin \theta e^{-i \varphi} \label {7-44} \end{align}\]
El componente imaginario en estas funciones de onda es algo desconcertante hasta que nos damos cuenta de que el módulo cuadrado de la función de onda tiene la interpretación física de una densidad de probabilidad, y el componente imaginario desaparece en el módulo.
\[|Y^1_1|^2 = |Y^{-1}_1|^2 = \frac {3}{8 \pi} \sin ^2 \theta \label {7-45}\]
En estas expresiones, que son idénticas, el ángulo\(\varphi \) nuevamente no aparece. No hay restricciones en las funciones de onda con respecto al ángulo\(\varphi\); es decir, la densidad de probabilidad se extiende uniformemente sobre todos los valores\(\varphi \) asociados con un particular\(\theta\). La\(\theta\) dependencia es una\(\sin^2\) función, que tiene un máximo a 90º y va a 0º como\(\theta\) va a 0º y 180º para ambos estados rotacionales como se muestra en la Figura\(\PageIndex{3}\).

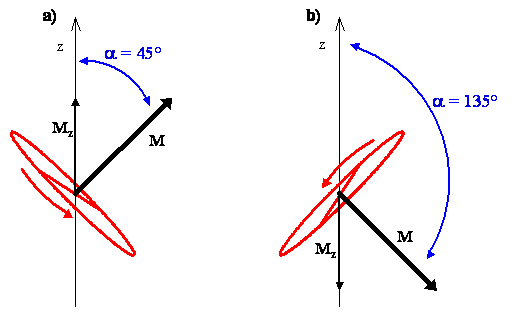
La interpretación clásica de la rotación asociada al vector de momento angular para el\(m_J = 1\) estado, que se inclina en un ángulo de 45º con respecto al eje z, dice que los posibles planos de rotación que contienen el eje internuclear de la molécula se alinean perpendicularmente al momento angular vector, como se muestra en la Figura\(\PageIndex{4a}\). La molécula está rotando en cualquiera de estos planos con igual probabilidad.
Para el\(m_J = -1\) estado, el vector de momento angular se encuentra en un ángulo\(\alpha\) = 135º del eje z, y los posibles planos de rotación que contienen el eje internuclear son perpendiculares a éste, como se muestra en la Figura\(\PageIndex{4b}\). Usando la regla de la mano derecha, la dirección de rotación es en sentido horario para el\(m_J = -1\) estado y en sentido antihorario para el\(m_J = 1\) estado.
Ejercicio\(\PageIndex{19}\)
Cinco estados tienen\(J = 2\). Calcular los ángulos que hacen los vectores de momento angulares para estos estados con respecto al eje z. Esboce un diagrama similar a la Figura\(\PageIndex{4}\) en el que los cinco vectores de momento angulares para el nivel de\(J = 2\) energía se colocan en el mismo diagrama. Describir cómo la molécula gira en relación con uno de estos vectores.


