9.1: La ecuación de Schrödinger para átomos de electrones múltiples
- Page ID
- 71126
En este capítulo, utilizaremos el átomo de helio como ejemplo específico de un átomo multielectrónico. La figura\(\PageIndex{1}\) muestra una representación esquemática de un átomo de helio con dos electrones cuyas coordenadas están dadas por los vectores\(r_1\) y\(r_2\). Los electrones están separados por una distancia\(r_{12} = |r_1-r_2|\). El origen del sistema de coordenadas se fija en el núcleo. Al igual que con el átomo de hidrógeno, los núcleos para los átomos de múltiples electrones son tanto más pesados que un electrón que se supone que el núcleo es el centro de masa. Fijar el origen del sistema de coordenadas en el núcleo nos permite excluir el movimiento traslacional del centro de masa de nuestro tratamiento mecánico cuántico.
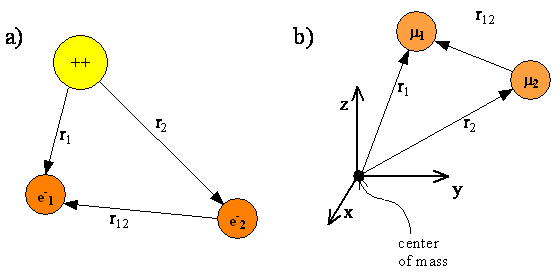
El operador hamiltoniano para el átomo de hidrógeno sirve como punto de referencia para escribir el operador hamiltoniano para átomos con más de un electrón. Comience con la misma forma general que usamos para el átomo de hidrógeno Hamiltoniano
\[\hat {H} = \hat {T} + \hat {V} \label {9-1}\]
Incluir un término de energía cinética para cada electrón y un término de energía potencial para la atracción de cada electrón cargado negativamente para el núcleo cargado positivamente y un término de energía potencial para la repulsión mutua de cada par de electrones cargados negativamente. El átomo de He Hamiltoniano es
\[ \hat {H} = -\dfrac {\hbar ^2}{2m_e} (\nabla ^2_1 + \nabla ^2_2) + V (r_1) + V (r_2) + V (r_{12}) \label {9-2}\]
donde
\[ V(r_1) = -\dfrac {2e^2}{4 \pi \epsilon _0 r_1} \label {9-3}\]
\[ V(r_2) = -\dfrac {2e^2}{4 \pi \epsilon _0 r_2} \label {9-4}\]
\[ V(r_{12}) = -\dfrac {e^2}{4 \pi \epsilon _0 r_{12}} \label {9-5}\]
La ecuación se\(\ref{9-2}\) puede extender a cualquier átomo o ión incluyendo términos para los electrones adicionales y reemplazando la carga nuclear de He +2 con una carga general\(Z\); p.
\[V(r_1) = -\dfrac {Ze^2}{4 \pi \epsilon _0 r_1} \label {9-6}\]
Ecuación\(\ref{9-2}\) entonces se convierte
\[\hat {H} = -\dfrac {\hbar ^2}{2m_e} \sum _i \nabla ^2_i + \sum _i V (r_i) + \sum _{i \ne j} V (r_{ij}) \label {9-7}\]
Ejercicio\(\PageIndex{1}\)
Refiriéndose a la Ecuación\(\ref{9-7}\), explicar el significado de las tres sumaciones y escribir expresiones para los\(V(r_{ij})\) términos\(V(r_i)\) y.
Ejercicio\(\PageIndex{2}\)
Escriba el multielectrón Hamiltoniano (por ejemplo, Ecuación\(\ref{9-2}\)) para un átomo de boro.
Cada electrón tiene su propio término de energía cinética en Ecuaciones\(\ref{9-2}\) y\(\ref{9-7}\). Para un átomo como el sodio habría\(\nabla ^2_1 , \nabla ^2_2 , \cdot , \nabla ^2_{11}\). La otra gran diferencia entre los sistemas de electrones simples y los sistemas de múltiples electrones es la presencia de los\(V(r_{ij})\) términos que contienen\(1/r_{ij}\), donde\(r_{ij}\) está la distancia entre electrones\(i\) y\(j\). Estos términos dan cuenta de la repulsión electrón-electrón que esperamos entre partículas con carga similar.
Dado lo que hemos aprendido de los sistemas mecánicos cuánticos anteriores que hemos estudiado, predecimos que las soluciones exactas a la ecuación de Schrödinger multielectrón en Ecuación\(\ref{9-7}\) consistirían en una familia de funciones de onda multi-electrón, cada una con un valor propio de energía asociado. Estas funciones de onda y energías describirían los estados terrestres y excitados del átomo de múltiples electrones, así como las ondas de hidrógeno y sus energías asociadas describen los estados terrestres y excitados del átomo de hidrógeno. También predeciríamos que los números cuánticos estarían involucrados.
El hecho de que los electrones interactúen a través de su repulsión de Coulomb significa que una función de onda exacta para un sistema de múltiples electrones sería una sola función que depende simultáneamente de las coordenadas de todos los electrones; es decir, una función de onda multielectrónica,\(\psi (r_1, r_2, \cdots r_i)\). El módulo al cuadrado de tal función de onda describiría la probabilidad de encontrar los electrones (aunque no específicos) en una ubicación designada en el átomo. Alternativamente,\(ne |\psi |^2\) describiría la cantidad total de densidad electrónica que estaría presente en un punto particular en el átomo de múltiples electrones. Todos los electrones se describen simultáneamente mediante una función de onda multielectrónica, por lo que la cantidad total de densidad electrónica representada por la función de onda es igual al número de electrones en el átomo.
Todos los electrones se describen simultáneamente mediante una función de onda multielectrónica, por lo que la cantidad total de densidad electrónica representada por la función de onda es igual al número de electrones en el átomo.
Desafortunadamente, los términos de repulsión de Coulomb hacen imposible encontrar una solución exacta a la ecuación de Schrödinger para muchos átomos y moléculas de electrones aunque solo haya dos electrones. Las aproximaciones más básicas a las soluciones exactas implican escribir una función de onda multielectrónica como un producto simple de las funciones de onda de un solo electrón, y obtener la energía del átomo en el estado descrito por esa función de onda como la suma de las energías de los componentes de un electrón.
\[\psi (r_1, r_2, \cdots , r_i) \approx \varphi _1 (r_1) \varphi _2 (r_2) \cdots \varphi _i(r_i) \label {9-8}\]
Al escribir la función de onda multielectrónica como producto de funciones de un solo electrón, transformamos conceptualmente un átomo de múltiples electrones en una colección de electrones individuales ubicados en orbitales individuales cuyas características espaciales y energías se pueden identificar por separado. Para los átomos estas funciones de onda de un solo electrón se denominan orbitales atómicos. Para las moléculas, como veremos en el próximo capítulo, se les llama orbitales moleculares. Si bien se puede aprender mucho de tal análisis, es importante tener en cuenta que una imagen tan discreta y compartimentada de los electrones es una aproximación, aunque poderosa.


