10.1: La aproximación Nacido-Oppenheimer

La aproximación Born-Oppenheimer es uno de los conceptos básicos que subyacen a la descripción de los estados cuánticos de las moléculas. Esta aproximación permite separar el movimiento de los núcleos y el movimiento de los electrones. Esta no es una idea nueva para nosotros. Ya hicimos uso de esta aproximación en el modelo de partículas en caja cuando explicamos los espectros de absorción electrónica de los tintes de cianina sin considerar el movimiento de los núcleos. Luego discutimos el movimiento traslacional, rotacional y vibracional de los núcleos sin incluir el movimiento de los electrones. En este capítulo examinaremos más de cerca la significación y consecuencias de esta importante aproximación. Nota, en esta discusión nuclear se refiere a los núcleos atómicos como partes de moléculas no a la estructura interna del núcleo.

La aproximación Born-Oppenheimer descuida el movimiento de los núcleos atómicos al describir los electrones en una molécula. La base física para la aproximación Born-Oppenheimer es el hecho de que la masa de un núcleo atómico en una molécula es mucho mayor que la masa de un electrón (más de 1000 veces). Debido a esta diferencia, los núcleos se mueven mucho más lentamente que los electrones. Además, debido a sus cargos opuestos, existe una fuerza de atracción mutua de

\[\dfrac{Ze^2}{r^2}\]

actuando sobre un núcleo atómico y un electrón. Esta fuerza hace que ambas partículas sean aceleradas. Dado que la magnitud de la aceleración es inversamente proporcional a la masa, a = f/m, la aceleración de los electrones es grande y la aceleración de los núcleos atómicos es pequeña; la diferencia es un factor de más de 1000. En consecuencia, los electrones se mueven y responden a las fuerzas muy rápidamente, y los núcleos no lo son. Te puedes imaginar correr una carrera de 100 yardas contra alguien cuya aceleración es 1000 veces mayor que la tuya. Esa persona literalmente podría correr círculos a tu alrededor. Entonces una buena aproximación es describir los estados electrónicos de una molécula pensando que los núcleos no se mueven, es decir, que son estacionarios. Los núcleos, sin embargo, pueden estar estacionarios en diferentes posiciones, por lo que la función de onda electrónica puede depender de las posiciones de los núcleos a pesar de que se descuida su movimiento.

Ahora miramos las matemáticas para ver qué se hace al resolver la ecuación de Schrödinger después de hacer la aproximación Born-Oppenheimer. Para una molécula diatómica como ejemplo, el operador hamiltoniano se agrupa en tres términos

\[\hat {H} (r, R) = \hat {T}_{nuc} (R) + \dfrac {e^2}{4\pi \epsilon _0} \dfrac {Z_A Z_B}{R} + \hat {H} _{elec} (r,R) \label {10-1}\]

donde

\[T_{nuc} (R) = -\dfrac {\hbar^2}{2m_A} \nabla ^2_A - \dfrac {\hbar ^2}{2m_B} \nabla ^2_B \label {10-2}\]

y

\[\hat {H} _{elec} (r, R) = \dfrac {- \hbar ^2}{2m} \sum \limits _i \nabla ^2_i + \dfrac {e^2}{4 \pi \epsilon _0} \left ( -\sum \limits _i \dfrac {Z_A}{r_{Ai}} - \sum \limits _i \dfrac {Z_B}{r_{Bi}} + \dfrac {1}{2} \sum \limits _i \sum \limits _{j \ne i} \dfrac {1}{r_{ij}}\right ) \label {10-3}\]

En la Ecuación\ ref {10-1}, el primer término representa la energía cinética de los núcleos, el segundo término representa la repulsión de Coulomb de los dos núcleos, y el tercer término representa la contribución a la energía de los electrones, que consiste en su energía cinética, repulsión mutua entre sí, y atracción por los núcleos. El tipo de negrilla se usa para representar eso\(r\) y\(R\) son vectores que especifican las posiciones de todos los electrones y todos los núcleos, respectivamente.

Ejercicio\(\PageIndex{1}\)

Define todos los símbolos en Ecuaciones\ ref {10-1} a través de\ ref {10-3}.

Ejercicio\(\PageIndex{2}\)

Explique por qué el factor de 1/2 aparece en el último término en la Ecuación\ ref {10-3}.

La aproximación Born-Oppenheimer dice que los términos de energía cinética nuclear en el hamiltoniano completo, Ecuación\ ref {10-1}, se pueden descuidar en la resolución de las funciones de onda y energías electrónicas. En consecuencia, la función de onda electrónica\(\varphi _e (r,R)\) se encuentra como una solución a la ecuación electrónica de Schrödinger:

\[\hat {H} _{elec} (r, R) \varphi _e (r, R) = E_e (R) \varphi _e (r, R) \label {10-4}\]

A pesar de que se descuiden los términos de energía cinética nuclear, la aproximación Born-Oppenheimer todavía toma en cuenta la variación en las posiciones de los núcleos para determinar la energía electrónica y la función de onda electrónica resultante depende de las posiciones nucleares,\(R\).

Como resultado de la aproximación Born-Oppenheimer, la función de onda molecular se puede escribir como un producto la Aproximación Born-Oppenheimer

\[\psi _{ne} (r, R) = X_{ne} (R) \varphi _e (r, R) \label {10-5}\]

Esta función de onda del producto se llama la función de onda Born-Oppenheimer. La función\(X_{ne} (R)\) es la función de onda vibracional, que es una función de las coordenadas nucleares\(R\) y depende tanto de los números o estados cuánticos vibracionales como electrónicos,\(n\) y\(e\), respectivamente. La función electrónica,\(\varphi _e (r, R) \), es una función tanto de las coordenadas nucleares como electrónicas, pero sólo depende del número cuántico electrónico o estado electrónico,\(e\). El movimiento de traslación y rotación no está incluido aquí. Las funciones de onda traslacional y rotacional simplemente multiplican las funciones vibracionales y electrónicas en la Ecuación\ ref {10-5} para darle una función de onda molecular completa cuando los movimientos traslacional y rotacional no están acoplados al movimiento vibracional y electrónico.

Aproximación de Crudo Nacido-Oppenheimer

En la Aproximación Crudo Nacido-Oppenheimer,\(R\) se establece igual a\(R_o\), la separación de equilibrio de los núcleos, y las funciones de onda electrónicas se toman como las mismas para todas las posiciones de los núcleos.

La energía electrónica,\(E_e (R)\), en la Ecuación\ ref {10-4} se combina con la repulsiva energía Coulomb de los dos núcleos, para formar la función de energía potencial que controla el movimiento nuclear como se muestra en la Figura\(\PageIndex{1}\).

\[ V_e (R) = E_e (R) + \dfrac {e^2}{4\pi \epsilon _0} \dfrac {Z_A Z_B}{R} \label {10-6}\]

En consecuencia, la ecuación de Schrödinger para el movimiento vibracional es

\[( \hat {T} _{nuc} (R) + V (R) )_{X_{ne}} (R) = E_{ne X_{ne}} (R) \label {10-7}\]

En el Capítulo 6, la energía potencial se aproximó como un potencial armónico dependiendo del desplazamiento,\(Q\), de los núcleos desde sus posiciones de equilibrio.

Figura\(\PageIndex{1}\): La función de energía potencial para una molécula diatómica.

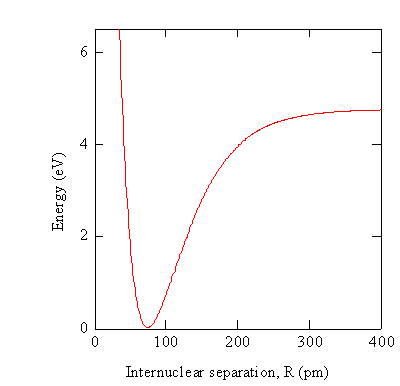
En la práctica, la ecuación electrónica de Schrödinger se resuelve utilizando aproximaciones\(R\) a valores particulares de para obtener las funciones de onda\(\varphi _e (r,R)\) y las energías potenciales\(V_e (R)\). Las energías potenciales se pueden graficar como se ilustra en la Figura\(\PageIndex{1}\).

El gráfico en la Figura\(\PageIndex{1}\) es la energía de una molécula diatómica en función de la separación internuclear, que sirve como la función de energía potencial para los núcleos. Cuando\(R\) es muy grande hay dos átomos que interactúan débilmente. A medida que\(R\) se hace más pequeña, la interacción se vuelve más fuerte, la energía se convierte en un gran valor negativo, y decimos que se forma un enlace entre los átomos. A valores muy pequeños de\(R\), la repulsión internuclear es muy grande por lo que la energía es grande y positiva. Esta función de energía controla el movimiento de los núcleos. Anteriormente, aproximamos esta función por un potencial armónico para obtener la descripción del movimiento vibracional en términos del modelo de oscilador armónico. También podrían usarse otras formas funcionales aproximadas, por ejemplo, el potencial Morse. La posición de equilibrio de los núcleos es donde esta función es mínima, es decir, at\(R = R_0\). Si obtenemos la función de onda en\(R = R_0\), y usamos esta función para todos los valores de\(R\), hemos empleado la aproximación Crudo Born-Oppenheimer.

Ejercicio\(\PageIndex{3}\)

Relacionar la ecuación\ ref {10-7} con la utilizada anteriormente en nuestra descripción de las vibraciones moleculares en términos del modelo de oscilador armónico.

En esta sección comenzamos con la ecuación de Schrödinger para una molécula diatómica y la separamos en dos ecuaciones, una ecuación electrónica de Schrödinger y una ecuación nuclear de Schrödinger. Para poder hacer la separación, tuvimos que hacer una aproximación. Tuvimos que descuidar el efecto de la energía cinética nuclear sobre los electrones. El hecho de que esta suposición funcione puede remontarse al hecho de que las masas nucleares son mucho mayores que la masa de electrones. Luego se utilizó la solución de la ecuación electrónica de Schrödinger para proporcionar la función de energía potencial para el movimiento nuclear. La solución a la ecuación nuclear de Schrödinger proporciona las ondas vibracionales y las energías.

Ejercicio\(\PageIndex{4}\)

Explicar la diferencia entre la aproximación Born-Oppenheimer y la aproximación Crudo Born-Oppenheimer.