5.2: Ecuaciones diferenciales ordinarias de segundo orden - Oscilaciones
- Page ID
- 70038
Nota
Esta sección también está disponible en formato de video: http://tinyurl.com/kq7mrcq
El movimiento de un péndulo sin fricción
Ahora usaremos lo aprendido hasta el momento para resolver un problema de relevancia en las ciencias físicas. Comenzaremos con el problema del péndulo, y como ya discutimos en la Sección 3.2, aunque el péndulo no sea particularmente interesante como aplicación en química, el tema de las oscilaciones es de gran interés debido a que los átomos en las moléculas vibran alrededor de sus enlaces.
El problema del péndulo se introdujo en la Figura 3.5, la cual se vuelve a imprimir a continuación:
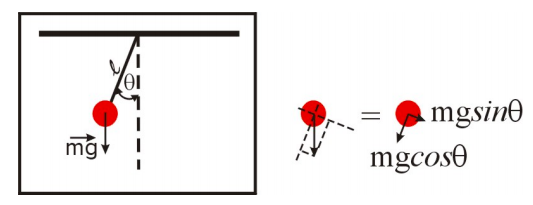
Si tomaste un curso universitario de física, puedes reconocer que la segunda ley de Newton rinde:
\[ \label{eqn2} ml\frac{d^2\theta}{dt^2}+mg\sin{\theta}=0\]
Esta, desafortunadamente, es una ecuación diferencial no lineal (la variable dependiente\(\theta\),, aparece como argumento de una función trascendental). Como discutimos en la Sección 3.2, esta ODE no tiene solución analítica. Es posible resolver esta ecuación numéricamente (y la harás en el laboratorio), pero no podemos obtener una ecuación que sea la solución de esta ODE. También discutimos que podemos obtener soluciones analíticas si asumimos que el ángulo\(\theta\) es pequeño en todo momento. Esto quiere decir que la solución que obtenemos es válida sólo si el péndulo oscila muy cerca de la línea normal al techo. Puede estar pensando que estudiar un sistema así es aburrido e inútil, pero nuevamente, como discutimos en la Sección 3.2, para la mayoría de las moléculas a temperaturas moderadas el desplazamiento de los átomos alrededor de su posición de equilibrio es muy pequeño. Es por ello que estudiar oscilaciones de sistemas cercanos al equilibrio tiene sentido para un químico.
Ya discutimos que si\(\theta<<1\), entonces\(\sin{\theta}\approx\theta\) (ver Figura 3.4). La ecuación\ ref {eqn2} puede simplificarse a:
\[ \frac{d^2\theta}{dt^2}+\frac{g}{l}\theta=0\]
Esta ecuación es lineal en\(\theta\), es homogénea, y tiene coeficientes constantes (\(g\)es la aceleración de la gravedad y\(l\) la longitud de la varilla). La ecuación auxiliar de esta ODE es:
\[\alpha^2+\frac{g}{l}=0 \nonumber\]
y por lo tanto,
\[\alpha=\pm i \sqrt{\frac{g}{l}} \nonumber\]
La solución general es
\[\theta(t)=c_1 e^{\alpha_1t}+c_2 e^{\alpha_2t} \nonumber\]
\[\theta(t)=c_1 e^{i(g/l)^{1/2}t}+c_2 e^{-i(g/l)^{1/2}t} \nonumber\]
Obtendremos los valores de las constantes arbitrarias a partir de las condiciones iniciales. Supongamos que en el tiempo cero el valor de\(\theta\) era\(\theta_0<<1\), y el valor de\(d\theta/dt\), que es una medida de la velocidad, era\(\theta'(0)=0\). Físicamente, significa que en el tiempo cero estamos manteniendo quieto el péndulo. En este punto podemos usar las relaciones de Euler para simplificar nuestro resultado en un coseno y un seno, o usar las condiciones iniciales y usar la relación de Euler más tarde. De cualquier manera funcionará, y cómo eliges proceder es una cuestión de gusto personal. Apliquemos ahora las condiciones iniciales:
\[\theta(t)=c_1 e^{i(g/l)^{1/2}t}+c_2 e^{-i(g/l)^{1/2}t}\rightarrow\theta(0)=c_1+c_2=\theta_0 \nonumber\]
\[\theta'(t)=c_1i(g/l)^{1/2} e^{i(g/l)^{1/2}t}-c_2i(g/l)^{1/2} e^{-i(g/l)^{1/2}t} \nonumber\]
\[\theta'(0)=c_1i(g/l)^{1/2}-c_2i(g/l)^{1/2}=0\rightarrow c_1=c_2 \nonumber\]
Por lo tanto\(c_1=c_2=\theta_0/2\),, y nuestra solución particular es:
\[\theta(t)=\frac{\theta_0}{2}\left(e^{i(g/l)^{1/2}t}+e^{-i(g/l)^{1/2}t}\right) \nonumber\]
Por la relación de Euler sabemos que\(e^{ix}+e^{-ix}=2cos{x}\), entonces
\[ \label{eqn3} \theta(t)=\theta_0\cos{\left(\left(\frac{g}{l}\right) ^{1/2}t\right)}\]
Esta es, por supuesto, la función periódica familiar que viste en tu curso de física. Recuerden que llegamos hasta aquí asumiendo\(\theta<<1\) en todo momento.
Como vimos en la Sección 1.4, el periodo de la función\(\cos(nx)\) es\(2\pi/n\). El periodo de la función\(\theta_0\cos{\left(\left(\frac{g}{l}\right) ^{1/2}t\right)}\) es por lo tanto\(P=2\pi \left(\frac{l}{g} \right)^{1/2}\). El periodo tiene unidades de tiempo, y nos dice el tiempo que tarda el péndulo en completar un ciclo completo (ver Figura\(\PageIndex{2}\)).
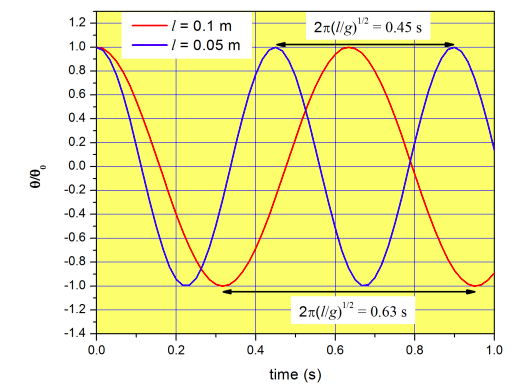
También podemos calcular la frecuencia del movimiento, que es solo el recíproco del periodo. Si el periodo es la cantidad de tiempo que necesitas esperar para completar un ciclo completo, el recíproco es el número de ciclos por unidad de tiempo. Por ejemplo, si toma un péndulo con\(l=0.1 m\) 0.63 segundos para completar un ciclo, esto significa que obtenemos 1.58 ciclos por segundo. La frecuencia tiene unidades de tiempo recíproco.
El hecho de que la péndula con diferentes longitudes tenga diferentes períodos fue utilizado por una mente muy creativa para producir la hermosa exhibición exhibida en el vestíbulo del edificio PSF en ASU (justo al otro lado de los ascensores). Hay algunos videos en YouTube que demuestran la idea (buscar ondas de péndulo), pero el del departamento de física de ASU es mucho más impresionante, así que ve a comprobarlo si aún no lo has hecho.
El péndulo en un medio viscoso
El problema que acabamos de ver suponía que no había fricción, por lo que el péndulo oscilará para siempre sin cambiar la amplitud. Hagamos el problema más realista desde el punto de vista físico y agreguemos un término que dé cuenta de la resistencia a la fricción. La fuerza debida a la fricción suele ser proporcional a la velocidad, por lo que esta nueva fuerza introduce un término que depende de la primera derivada de\(\theta\):
\[ \frac{d^2\theta}{dt^2}+\gamma \frac{d\theta}{dt}+\frac{g}{l}\theta=0\]
La constante\(\gamma\) depende del medio, y será mayor, por ejemplo, en agua (más fricción) que en el aire (menos fricción). La ecuación auxiliar es ahora
\[\alpha^2+\gamma \alpha+\frac{g}{l}=0 \nonumber\]
y las dos raíces son:
\[\alpha_{1,2}=\frac{-\gamma \pm\sqrt{\gamma^2-4g/l}}{2} \nonumber\]
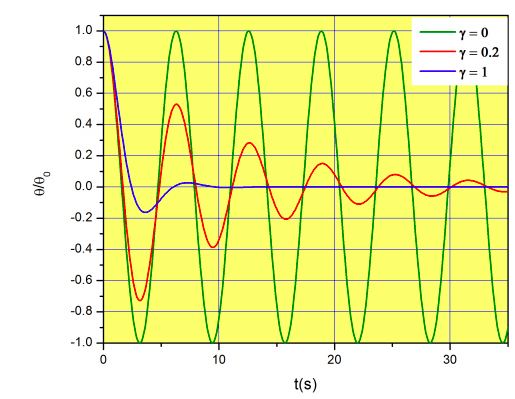
y vemos que el resultado dependerá de los valores relativos de\(\gamma^2\) y\(4g/l\). Analizaremos\(\gamma^2<4g/l\) primero el caso (régimen de baja fricción). Es útil pensar siempre en lo que uno espera antes de hacer alguna matemática. Piensa en el péndulo sin fricción, e imagina que haces el mismo experimento en el aire (fricción pequeña). ¿Cómo crees que se\(t\) vería la trama de\(\theta(t)\) vs?
Volviendo a las matemáticas, llamemos\(a=\sqrt{4g/l-\gamma^2}\) para simplificar la notación. En el caso de baja fricción,\(a\) será un número real. Por lo tanto, las dos raíces serán:
\[\alpha_{1,2}=\frac{-\gamma \pm ia}{2} \nonumber\]
y la solución general será
\[\theta(t)=c_1 e^{\alpha_1 t}+c_1 e^{\alpha_2 t} \nonumber\]
\[\theta(t)=c_1 e^{-\gamma t/2}e^{ia t/2}+c_2 e^{-\gamma t/2}e^{-ia t/2} \nonumber\]
\[\theta(t)=e^{-\gamma t/2}\left(c_1 e^{ia t/2}+c_2 e^{-ia t/2}\right) \nonumber\]
En este punto podemos usar las condiciones iniciales y usar la relación de Euler más tarde, o podemos usar las ecuaciones de Euler ahora y las condiciones iniciales más adelante. De cualquier manera debería funcionar.
\[\theta(t)=e^{-\gamma t/2}\left[\left(c_1 \cos{(ta/2)} +c_1 i \sin{(ta/2)}+c_2 \cos{(ta/2)} -c_2 i \sin{(ta/2)}\right)\right] \nonumber\]
\[\theta(t)=e^{-\gamma t/2}\left[(c_1+c_2) \cos{(ta/2)} +(c_1-c_2) i \sin{(ta/2)}\right] \nonumber\]
y las constantes de agrupamiento y redenominación:
\[\theta(t)=e^{-\gamma t/2}\left[c_3 \cos{(ta/2)} +c_4\sin{(ta/2)}\right] \nonumber\]
Ahora vamos a evaluar\(c_3\) y\(c_4\) a partir de las condiciones iniciales. Asumamos de nuevo eso\(\theta(0)=\theta_0\) y\(\theta'(0)=0\). Evaluando la ecuación anterior en\(t=0\):
\[\theta(0)=c_3=\theta_0 \nonumber\]
por lo que tenemos
\[\theta(t)=e^{-\gamma t/2}\left[\theta_0 \cos{(\frac{ta}{2})} +c_4\sin{(\frac{ta}{2})}\right] \nonumber\]
\[\theta'(t)=e^{-\gamma t/2}\left[-\frac{\theta_0 a}{2} \sin{(\frac{ta}{2})} +\frac{c_4 a}{2}\cos{(\frac{ta}{2})}\right]-\frac{\gamma}{2}e^{-\gamma t/2}\left[\theta_0 \cos{(\frac{ta}{2})} +c_4\sin{(\frac{ta}{2})}\right] \nonumber\]
\[\theta'(0)=c_4\frac{a}{2}-\theta_0\frac{\gamma}{2}=0 \nonumber\]
\[c_4=\frac{\gamma \theta_0}{a} \nonumber\]
y por lo tanto
\[\theta(t)=e^{-\gamma t/2}\left[\theta_0 \cos{\left(\frac{ta}{2}\right)} +\frac{\gamma \theta_0}{a}\sin{\left(\frac{ta}{2}\right)}\right] \nonumber\]
\[ \theta(t)=\theta_0 e^{-\gamma t/2}\left[ \cos{\left(\frac{ta}{2}\right)} +\frac{\gamma }{a}\sin{\left(\frac{ta}{2}\right)}\right]\]
Si todo salió bien esta ecuación debería simplificarse a la Ecuación\ ref {eqn3} para el caso\(\gamma=0\). Recordemos eso\(a=\sqrt{4g/l-\gamma^2}\), así que si\(\gamma=0\):
\[\theta(t)=\theta_0 \left[ \cos{\left(\frac{ta}{2}\right)}\right] \nonumber\]
\[\theta(t)=\theta_0 \left[ \cos{\left(\sqrt{\frac{g}{l}}t\right)}\right] \nonumber\]
Esto por supuesto no prueba que nuestra solución sea correcta, pero siempre es bueno ver que recuperamos una ecuación conocida para un caso particular (en este caso\(\gamma=0\)).
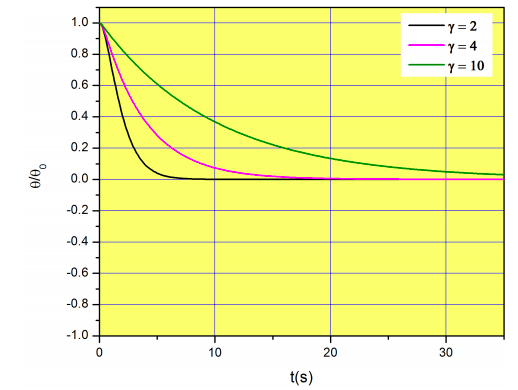
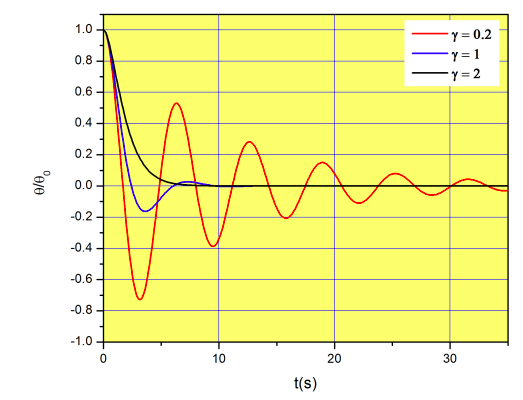
La figura\(\PageIndex{3}\) muestra\(\theta(t)/\theta_0\) para tres casos con\(g/l=1\) (es decir, un cordón de 9.8 m de longitud) y valores crecientes de fricción. Recuerden que estamos asumiendo que eso\(\theta\) es pequeño.
Hasta el momento hemos analizado el caso\(\gamma^2<4g/l\). A medida que aumentemos el coeficiente de fricción, llegaremos al punto donde\(\gamma^2=4g/l\). Mira Figura\(\PageIndex{3}\), y piensa en lo que verías cuando esto suceda. Matemáticamente, tendremos dos raíces repetidas:
\[\alpha_{1,2}=\frac{-\gamma \pm\sqrt{\gamma^2-4g/l}}{2}=-\frac{\gamma }{2} \nonumber\]
así\(\theta(t)=e^{-\gamma t/2}\) es una solución, pero necesitamos encontrar una solución independiente a través del método de reducción del orden. Sabemos que la solución general será (Sección 2.2):
\[\theta(t)=(c_1+c_2 t)e^{-\gamma t/2} \nonumber\]
Las constantes arbitrarias se calcularán a partir de las condiciones iniciales:
\[\theta(0)=(c_1)=\theta_0 \nonumber\]
\[\theta'(t)=-\frac{\gamma}{2}(\theta_0+c_2 t)e^{-\gamma t/2}+c_2e^{-\gamma t/2} \nonumber\]
\[\theta'(0)=-\frac{\gamma}{2}(\theta_0)+c_2=0 \nonumber\]
\[c_2=\frac{\gamma}{2}\theta_0 \nonumber\]
Por lo tanto,
\[\theta(t)=(c_1+c_2 t)e^{-\gamma t/2} \nonumber\]
\[\theta(t)=(\theta_0+\frac{\theta_0 \gamma}{2} t)e^{-\gamma t/2}=\theta_0(1+\frac{\gamma}{2} t)e^{-\gamma t/2} \nonumber\]
El comportamiento de\(\theta(t)\) se muestra en Figura\(\PageIndex{4}\) en negro. Este régimen se llama amortiguado críticamente porque representa el punto donde las oscilaciones ya no ocurren a medida que\(\gamma\) aumenta. Si seguimos aumentando el coeficiente de fricción, el péndulo se\(\theta=0\) acercará cada vez más lento, pero nunca cruzará hacia el otro lado (\(\theta<0\)). Encontremos la expresión matemática para\(\theta(t)\) para el caso\(\gamma^2>4g/l\). Las dos raíces son ahora diferentes y reales:
\[\alpha_{1,2}=\frac{-\gamma \pm\sqrt{\gamma^2-4g/l}}{2} \nonumber\]
y la solución general es, por lo tanto
\[\theta(t)=c_1e^{\alpha_1t}+c_2e^{\alpha_2t} \nonumber\]
\[\theta(t)=c_1e^{(-\gamma+b)t/2}+c_2e^{(-\gamma-b)t/2}; \; b=\sqrt{\gamma^2-4g/l} \nonumber\]
La primera condición inicial es\(\theta(0)=\theta_0\):
\[\theta(0)=c_1+c_2=\theta_0 \nonumber\]
La segunda condición inicial es\(\theta'(t)=0\):
\[\theta'(t)=c_1\left(\frac{-\gamma+b}{2}\right)e^{(-\gamma+b)t/2}+c_2\left(\frac{-\gamma-b}{2}\right)e^{(-\gamma-b)t/2} \nonumber\]
\[\theta'(0)=c_1\left(\frac{-\gamma+b}{2}\right)+c_2\left(\frac{-\gamma-b}{2}\right)=0\nonumber \]
\[\theta'(0)=-(c_1+c_2)\gamma+(c_1-c_2)b=0 \nonumber\]
la primera condición inicial cedió\(c_1+c_2=\theta_0\) así
\[\theta'(0)=-\theta_0\gamma+(c_1-c_2)b=0 \nonumber\]
\[(c_1-c_2)=\theta_0\gamma/b \nonumber\]
Las dos condiciones iniciales dieron dos relaciones entre\(c_1\) y\(c_2\):
\[c_1+c_2=\theta_0 \nonumber\]
\[(c_1-c_2)=\theta_0\gamma/b \nonumber\]
Resolviendo este sistema de dos ecuaciones con dos incógnitas:
\[c_1=\frac{\theta_0}{2}\left(1+\frac{\gamma}{b} \right) \nonumber\]
\[c_2=\frac{\theta_0}{2}\left(1-\frac{\gamma}{b} \right) \nonumber\]
Y finalmente podemos escribir la solución particular como:
\[\theta(t)=c_1e^{(-\gamma+b)t/2}+c_2e^{(-\gamma-b)t/2}; \; b=\sqrt{\gamma^2-4g/l} \nonumber\]
\[\theta(t)=\frac{\theta_0}{2}\left(1+\frac{\gamma}{b} \right)e^{(-\gamma+b)t/2}+\frac{\theta_0}{2}\left(1-\frac{\gamma}{b} \right)e^{(-\gamma-b)t/2}; \; b=\sqrt{\gamma^2-4g/l} \nonumber\]
\[ \theta(t)=\frac{\theta_0}{2}e^{-\gamma t/2}\left[\left(1+\frac{\gamma}{b} \right)e^{b t/2}+\left(1-\frac{\gamma}{b} \right)e^{-b t/2}\right]\]
La figura\(\PageIndex{5}\) muestra resultados con\(g/l=1\), y tres valores diferentes de\(\gamma\). Aviso que\(\gamma=2\) corresponde al régimen críticamente amortiguado.