5.4: Un ejemplo en Mecánica Cuántica
- Page ID
- 70025
El postulado principal de la mecánica cuántica establece que el estado de un sistema mecánico cuántico es especificado por una función llamada función de onda. La función de onda es una función de las coordenadas de la partícula (la posición) y el tiempo. A menudo nos ocupamos de estados estacionarios, es decir, estados cuya energía no depende del tiempo. Por ejemplo, a temperatura ambiente y en ausencia de radiación electromagnética como la luz UV, la energía del único electrón en el átomo de hidrógeno es constante (la energía del orbital 1s). En este caso, toda la información sobre el estado de la partícula está contenida en una función independiente del tiempo\(\psi (\textbf{r})\), donde\(\textbf{r}\) es un vector que define la posición de la partícula. En la Sección 2.3 mencionamos brevemente que se\(|\psi|^2 = \psi^* \psi\) puede interpretar en términos de la probabilidad de encontrar el electrón en diferentes regiones del espacio. Debido a que la probabilidad de encontrar la partícula en algún lugar del universo es 1, la función de onda necesita normalizarse (es decir, la integral de\(|\psi|^2\) sobre todo el espacio tiene que ser igual a 1).
La ecuación fundamental en la mecánica cuántica se conoce como la ecuación de Schrödinger, que es una ecuación diferencial cuyas soluciones son las funciones de onda. Para una partícula de masa que\(m\) se mueve en una dimensión en un campo potencial descrito por\(U(x)\) la ecuación de Schrödinger es:
\[ -\frac{\hbar^2}{2m} \frac{d^2\psi(x)}{dx^2}+U(x)\psi(x)=E \psi(x)\]
Observe que la posición de la partícula está definida por\(x\), porque estamos asumiendo un movimiento unidimensional. La constante\(\hbar\) (pronunciada “h-bar”) se define como\(h/(2\pi)\), donde\(h\) es la constante de Plank. \(U(x)\)es la energía potencial a la que se somete la partícula, y depende de las fuerzas involucradas en el sistema. Por ejemplo, si estuviéramos analizando el átomo de hidrógeno, la energía potencial sería debida a la fuerza de interacción entre el protón (cargado positivamente) y el electrón (cargado negativamente), que depende de su distancia. La constante\(E\) es la energía total, igual a la suma de las energías potenciales y cinéticas.
Esto será confuso hasta que empecemos a ver algunos ejemplos, así que no te desanimes y ten paciencia. Empecemos discutiendo el sistema mecánico cuántico más simple (desde el punto de vista matemático). Nuestro sistema consiste en una partícula de masa\(m\) que puede moverse libremente en una dimensión entre dos “paredes”. Las paredes son impenetrables, y por lo tanto la probabilidad de que encuentres la partícula fuera de esta caja unidimensional es cero. Esto no es muy diferente de una pelota de ping-pong que rebota dentro de una habitación. No importa lo duro que rebotes la pelota contra la pared, nunca la encontrarás del otro lado. No obstante, veremos que para las partículas microscópicas (masa pequeña), el sistema se comporta de manera muy diferente que para las partículas macroscópicas (la pelota de ping-pong). El comportamiento de los sistemas macroscópicos es descrito por las leyes de lo que llamamos mecánica clásica, mientras que el comportamiento de las moléculas, átomos y partículas subatómicas es descrito por las leyes de la mecánica cuántica. El problema que acabamos de describir se conoce como el problema de la “partícula en la caja”, y se puede extender a más dimensiones (por ejemplo, la partícula se puede mover en una caja 3D) o geometrías (por ejemplo, la partícula puede moverse en la superficie de una esfera, o dentro del área de un círculo).
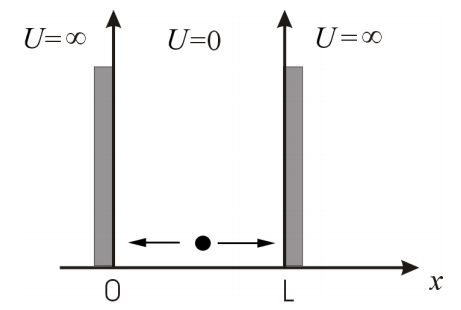
La partícula en una caja unidimensional
Comenzaremos con el caso más simple, que es un problema conocido como 'la partícula en una caja unidimensional' (Figura\(\PageIndex{1}\)). Se trata de un problema físico simple que, como veremos, proporciona una descripción rudimentaria de moléculas lineales conjugadas. En este problema, se permite que la partícula se mueva libremente en una dimensión dentro de una 'caja' de longitud\(L\). En este contexto, 'libremente' significa que la partícula no está sujeta a ninguna fuerza, por lo que la energía potencial dentro de la caja es cero. No se permite que la partícula se mueva fuera de la caja, y físicamente, garantizamos que esto es cierto al imponer una energía potencial infinita en los bordes de la caja (\(x = 0\)y\(x = L\)) y fuera de la caja (\(x < 0\)y\(x > L\)).
\[U(x)=\left\{\begin{matrix} \infty & x<0 \\ 0 & 0<x<L\\ \infty & x>L \end{matrix}\right. \nonumber\]
Debido a que la energía potencial fuera de la caja es infinito, la probabilidad de encontrar la partícula en estas regiones es cero. Esto significa que\(\psi(x)=0\) si\(x>L\) o\(x<0\). ¿Y\(\psi(x)\) dentro de la caja? Para encontrar las funciones de onda que describen los estados de un sistema, tenemos que resolver la ecuación de Schrödinger:
\[-\frac{\hbar^2}{2m} \frac{d^2\psi(x)}{dx^2}+U(x)\psi(x)=E \psi(x) \nonumber\]
Dentro de la caja\(U(x)=0\), así:
\[-\frac{\hbar^2}{2m} \frac{d^2\psi(x)}{dx^2}=E \psi(x) \nonumber\]
\[ \label{eqn1} \frac{\hbar^2}{2m} \frac{d^2\psi(x)}{dx^2}+ E\psi(x)=0\]
Recuerda que\(\hbar\) es una constante,\(m\) es la masa de la partícula (también constante), y\(E\) la energía. La energía de la partícula es una constante en el sentido de que no es una función de\(x\). Veremos que hay muchos (de hecho infinitos) valores posibles para la energía de la partícula, pero estos son números, no funciones de\(x\). Con todo esto en mente, ojalá reconozcas que la ecuación de Schrödinger para la partícula unidimensional en una caja es una ODE de segundo orden homogénea con coeficientes constantes. ¿Tenemos alguna condición inicial o límite? De hecho lo hacemos, porque la función de onda necesita ser una función continua de\(x\). Esto significa que no puede haber saltos repentinos de densidad de probabilidad cuando se mueve a través del espacio. En particular en este caso, significa que\(\psi(0)=\psi(L)=0\), porque la probabilidad de encontrar la partícula fuera de la caja es cero.
Vamos a resolver Ecuación\ ref {eqn1}. Necesitamos encontrar las funciones\(\psi(x)\) que satisfagan a la ODE. La ecuación auxiliar es (recuerde que\(m, \hbar, E\) son constantes positivas):
\[\frac{\hbar^2}{2m}\alpha^2+E=0 \nonumber\]
\[\alpha=\pm i \sqrt{\frac{2mE}{\hbar^2}} \nonumber\]
y la solución general es, por lo tanto:
\[\psi(x)=c_1e^{i \sqrt{\frac{2mE}{\hbar^2}}x}+c_2e^{-i \sqrt{\frac{2mE}{\hbar^2}}x} \nonumber\]
Porque\(\psi(0)=0\):
\[\psi(x)=c_1+c_2=0\rightarrow c_1=-c_2 \nonumber\]
\[\psi(x)=c_1\left(e^{i \sqrt{\frac{2mE}{\hbar^2}}x}-e^{-i \sqrt{\frac{2mE}{\hbar^2}}x}\right) \nonumber\]
Esto se puede simplificar usando las relaciones de Euler:\(e^{ix}-e^{-ix}=2i\sin{x}\)
\[\psi(x)=c_1(2i)\sin{\left(\sqrt{\frac{2mE}{\hbar^2}}x\right)} \nonumber\]
\[\psi(x)=A\sin{\left(\sqrt{\frac{2mE}{\hbar^2}}x\right)} \nonumber\]
En el último paso reconocimos que\(2ic_1\) es una constante, y la llamamos\(A\).
La segunda condición límite es\(\psi(L)=0\):
\[\psi(L)=A\sin{\left(\sqrt{\frac{2mE}{\hbar^2}}L\right)}=0 \nonumber\]
Podemos hacer\(A=0\), pero esto dará como resultado que la función de onda sea cero en todos los valores de\(x\). Esto es lo que antes llamábamos la 'solución trivial', y aunque es una solución desde el punto de vista matemático, no lo es cuando pensamos en la física del problema. Si\(\psi(x)=0\) la probabilidad de encontrar la partícula dentro de la caja es cero. No obstante, el problema establece que la partícula no se puede encontrar afuera, por lo que se tiene que encontrar dentro con una probabilidad de 1. Esto significa que no\(\psi(x)=0\) es una solución físicamente aceptable dentro de la caja, y nos vemos obligados a considerar las situaciones en las que
\[\sin{\left(\sqrt{\frac{2mE}{\hbar^2}}L\right)}=0 \nonumber\]
Sabemos que la función\(\sin{x}\) es cero en valores de\(x\) que son cero, o múltiplos de\(\pi\):
\[\left(\sqrt{\frac{2mE}{\hbar^2}}L\right)=\pi,2\pi, 3\pi...=n\pi\;(n=1,2,3..\infty) \nonumber\]
Esto significa que nuestra solución es:
\[\psi(x)=A\sin{\left(\frac{n\pi}{L}x\right)} \; (n=1,2,3...\infty) \nonumber\]
Observe que no lo consideramos\(n=0\) porque eso volvería\(\psi(x)\) a provocar que se desvaneciera dentro de la caja. Las funciones\(\psi(x)\) contienen información sobre el estado del sistema, y se denominan funciones propias. ¿Qué pasa con las energías?
\[\left(\sqrt{\frac{2mE}{\hbar^2}}L\right)=n\pi\rightarrow E=\left(\frac{n\pi}{L}\right)^2\frac{\hbar^2}{2m}\;(n=1, 2, 3...\infty) \nonumber\]
Las energías son los valores propios de esta ecuación. Observe que hay infinitas funciones propias, y cada una tiene un valor propio definido.
| \(n\) | \(\psi(x)\) | \(E\) |
|---|---|---|
| \ (n\) ">1 | \ (\ psi (x)\) ">\(A\sin{\left(\frac{\pi}{L}x\right)}\) | \ (E\) ">\(\left(\frac{\pi}{L}\right)^2\frac{\hbar^2}{2m}\) |
| \ (n\) ">2 | \ (\ psi (x)\) ">\(A\sin{\left(\frac{2\pi}{L}x\right)}\) | \ (E\) ">\(\left(\frac{2\pi}{L}\right)^2\frac{\hbar^2}{2m}\) |
| \ (n\) ">3 | \ (\ psi (x)\) ">\(A\sin{\left(\frac{3\pi}{L}x\right)}\) | \ (E\) ">\(\left(\frac{3\pi}{L}\right)^2\frac{\hbar^2}{2m}\) |
El estado de energía más bajo es descrito por la función de onda\(\psi=A\sin{\left(\frac{\pi}{L}x\right)}\), y su energía es\(\left(\frac{\pi}{L}\right)^2\frac{\hbar^2}{2m}\).
¿Qué pasa con la constante\(A\)? Matemáticamente, cualquier valor funcionaría, y ninguna de las condiciones límite impondría ninguna restricción a su valor. Físicamente, sin embargo, tenemos otra restricción que aún no hemos cumplido: la función de onda necesita ser normalizada. La integral de\(|\psi|^2\) sobre todo el espacio necesita ser 1 porque esta función representa una probabilidad.
\[\int_{-\infty}^{\infty}|\psi(x)|^2dx=1 \nonumber\]
Sin embargo,\(\psi(x)=0\) fuera de la caja, por lo que los rangos\(x<0\) y\(x>L\) no contribuyen a la integral. Por lo tanto:
\[\int_{0}^{L}|\psi(x)|^2dx=\int_{0}^{L}A^2\sin^2{\left(\frac{n\pi}{L}x\right)}dx=1 \nonumber\]
Calcularemos a\(A\) partir de esta condición de normalización. Usando las primitivas que se encuentran en la hoja de fórmulas, obtenemos:
\[\int_{0}^{L}\sin^2{\left(\frac{n\pi}{L}x\right)}dx=L/2 \nonumber\]
y por lo tanto
\[A=\sqrt{\frac{2}{L}} \nonumber\]
Ahora podemos anotar nuestra función de onda normalizada como:
\[ \psi(x)=\sqrt{\frac{2}{L}}\sin{\left(\frac{n\pi}{L}x\right)} \; (n=1,2,3...\infty) \]
¡Resolvimos nuestro primer problema en mecánica cuántica! Vamos a discutir lo que tenemos, y lo que significa. Primero, debido a que la energía potencial dentro de la caja es cero, la energía total es igual a la energía cinética de la partícula (es decir, la energía debido a que la partícula se mueve de izquierda a derecha o de derecha a izquierda). Una pelota de ping-pong dentro de una caja macroscópica puede moverse a cualquier velocidad que queramos, por lo que su energía cinética no se cuantifica. Sin embargo, si la partícula es un electrón, su energía cinética dentro de la caja puede adoptar solo valores cuantificados de energía:\(E=\left(\frac{n\pi}{L}\right)^2\frac{\hbar^2}{2m}\;(n=1, 2, 3...\infty)\). Curiosamente, la partícula no puede tener cero energía (no\(n=0\) es una opción), por lo que no puede estar en reposo (nuestra pelota de ping-pong puede tener cero energía cinética sin violar ninguna ley física). Si una pelota de ping-pong se mueve libremente dentro de la caja podemos encontrarla con igual probabilidad cerca de los bordes o cerca del centro. ¡No por un electrón en una caja unidimensional! La función\(|\psi(x)|^2\) para el estado de energía más baja (\(n=1\)) se representa en la Figura\(\PageIndex{2}\). La probabilidad de encontrar el electrón es mayor en el centro que en los bordes; nada como lo que esperamos de un sistema macroscópico. La gráfica es simétrica alrededor del centro de la caja, lo que significa que la probabilidad de encontrar la partícula en el lado izquierdo es la misma que encontrarla en el lado derecho. Esa es una buena noticia, porque el problema es verdaderamente simétrico, y no hay fuerzas extras que atraigan o repelen la partícula de la mitad izquierda o derecha a la caja.
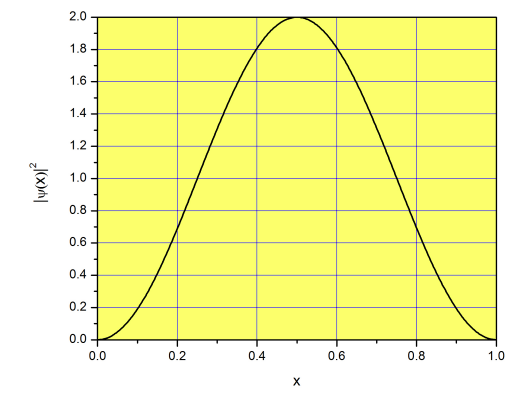
Mirando Figura\(\PageIndex{2}\), se puede pensar que la probabilidad de encontrar la partícula en el centro realmente 2. ¿Cómo puede ser esto? ¡Las probabilidades no pueden ser mayores a 1! Esto es una fuente importante de confusión entre los estudiantes, así que aclaremos lo que significa. La función no\(|\psi(x)|^2\) es una probabilidad, sino una densidad de probabilidad. Técnicamente, esto significa que\(|\psi(x)|^2dx\) es la probabilidad de encontrar la partícula entre\(x\) y\(x+dx\) (ver página para más detalles). Por ejemplo, la probabilidad de encontrar la partícula entre\(x=0.5\) y\(0.5001\) es\(\approx|\psi(0.5)|^2\times 0.0001= 0.0002\). Esto es aproximado porque\(\Delta x= 0.0001\) es pequeño, pero no infinitesimal. ¿Qué pasa con la probabilidad de encontrar la partícula entre\(x=0.5\) y\(0.6\)? Necesitamos integrar\(|\psi(x)|^2dx\) entre\(x=0.5\) y\(x=0.6\):
\[p(0.5<x<0.6)=\int_{0.5}^{0.6} |\psi(x)|^2dx\approx 0.2 \nonumber\]
Es importante destacar que
\[p(0<x<1)=\int_{0}^{1} |\psi(x)|^2dx=1 \nonumber\]
como debería ser el caso de una función de onda normalizada. Observe que estas probabilidades se refieren al estado de energía más bajo (\(n=1\)), y serán diferentes para los estados de energía creciente.
El problema de partículas en la caja también está disponible en formato de video: http://tinyurl.com/mjsmd2a
¿Dónde está la química?
Hasta ahora hablamos de un sistema que suena bastante alejado de todo lo que a nosotros (a los químicos) nos importa. Entendemos electrones en átomos, pero ¿electrones moviéndose en una caja unidimensional? Para ver por qué esto no es una idea tan loca, consideremos la molécula de caroteno (el pigmento naranja en las zanahorias). Sabemos que todos esos dobles enlaces están conjugados, lo que significa que los\(\pi\) electrones están deslocalizados y relativamente libres para moverse alrededor de los enlaces resaltados en rojo en la Figura\(\PageIndex{3}\).
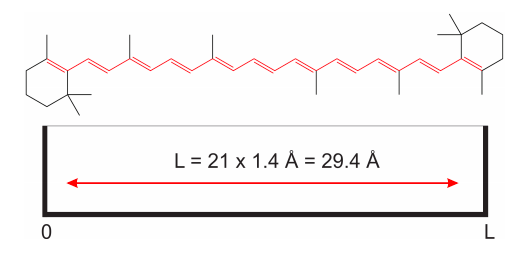
Debido a que la longitud de cada enlace carbono-carbono es de alrededor de 1.4 Å (Å significa angstrom, e igual\(10^{-10}m\)), podemos suponer que los\(\pi\) electrones se mueven dentro de una caja unidimensional de longitud\(L = 21\times 1.4\) Å\(= 29.4\) Å. Esto es obviamente una aproximación, ya que no es cierto que los electrones se muevan libremente sin estar sujetos a ninguna fuerza. Sin embargo, veremos que este sencillo modelo da una buena descripción semicuantitativa del sistema.
Ya resolvimos el problema de la partícula en una caja, y obtuvimos los siguientes valores propios:
\[ E=\left(\frac{n\pi}{L}\right)^2\frac{\hbar^2}{2m}\;(n=1, 2, 3...\infty) \label{eqn2}\]
Estas son las energías que se permite que tenga la partícula en la caja. En este caso, la partícula en cuestión es un electrón, así\(m\) es la masa de un electrón. Observe que tenemos todo lo que necesitamos para usar la Ecuación\ ref {eqn2}:\(\hbar = 1.0545 \times 10^{-34} m^2 kg\, s^{-1}\),\(m=9.109 \times 10^{-31}kg\), y\(L = 2.94 \times 10^{-9} m\). Esto nos permitirá calcular las energías permitidas para los\(\pi\) electrones en caroteno. Para\(n=1\) (el estado energético más bajo), tenemos:
\[E_1=\left(\frac{\pi}{L}\right)^2\frac{\hbar^2}{2m}=6.97 \times 10^{-21}J \nonumber\]
Joule es la unidad de energía, y\(1J = kg\times m^2\times s^{-2}\). Una manera muy fácil de recordar esto es recordar la ecuación de Einstein:\(E = mc^2\), que te dice que la energía es una masa multiplicada por el cuadrado de una velocidad (de ahí,\(1J = 1kg (1 m/s)^2\)). Volviendo a la Ecuación\ ref {eqn2}, las energías permitidas para\(\pi\) los electrones en caroteno son:
\[E_n=n^2\times6.97 \times 10^{-21}J\;(n=1, 2, 3...\infty) \nonumber\]
Observe que las energías aumentan rápidamente. ¡La energía del décimo nivel (\(E_{10}\)) es cien veces la energía del primero! El número de niveles es inifinito, pero claro que sabemos que los electrones llenarán los que son más bajos en energía. Esto es análogo al átomo de hidrógeno. Sabemos que hay un número infinito de niveles de energía, pero en ausencia de una fuente de energía externa sabemos que el electrón estará en el orbital 1s, que es el nivel de energía más bajo. Este electrón tiene un número infinito de niveles disponibles, pero necesitamos una fuente externa de energía si queremos que el electrón ocupe un estado energético superior. Los mismos conceptos se aplican a las moléculas. Como has aprendido en química general, no podemos tener más de dos electrones en un nivel dado, por lo que pondremos nuestros 22\(\pi\) electrones (2 por doble enlace) en los primeros 11 niveles (Figura\(\PageIndex{4}\), izquierda).

Podemos promover un electrón al primer nivel desocupado (en este caso\(n=12\)) mediante el uso de luz de la frecuencia apropiada (\(\nu\)). La energía de un fotón es\(E = h\nu\), donde\(h\) está la constante de Plank. Para que la molécula absorba la luz, la longitud de onda del haz de luz necesita coincidir exactamente con la brecha de energía entre el estado ocupado más alto (en este caso\(n=11\)) y el estado desocupado más bajo. La longitud de onda de la luz está relacionada con la frecuencia como:\(\lambda = c/\nu\), donde\(c\) está la velocidad de la luz. Por lo tanto, para producir el estado excitado mostrado en el lado derecho de la Figura\(\PageIndex{4}\), tenemos que usar luz de la siguiente longitud de onda:
\[E=E_{12}-E_{11}=h\nu=h c/\lambda\rightarrow \lambda=hc/(E_{12}-E_{11}) \nonumber\]
Recordemos eso\(E_n=n^2\times6.97 \times 10^{-21}J\), entonces\((E_{12}-E_{11})= (144-121)\times6.97 \times 10^{-21}J=1.60\times 10^{-19}J\). Por lo tanto,
\[\lambda = \frac{6.626\times10^{-34} J\,s\times 3\times10^8 m\, s^{-1}}{1.60\times 10^{-19}J}=1.24\times10^{-6}m=1,242 nm \nonumber\]
En el último paso expresamos el resultado en nanómetros (\(1nm=10^{-9}m\)), que es una unidad común para describir la longitud de onda de la luz en las regiones visible y ultravioleta del espectro electromagnético. En realidad es bastante fácil medir el espectro de absorción del caroteno. Solo necesitas tener una solución de caroteno, brillar la solución con luz de diferentes colores (longitudes de onda), y ver qué porcentaje de la luz se transmite. La luz que no se transmite es absorbida por las moléculas debido a transiciones como la que se muestra en la Figura\(\PageIndex{4}\). En realidad, la absorción de caroteno ocurre realmente a 497 nm, no a 1,242 nm. La discrepancia se debe a las enormes aproximaciones de la partícula en el modelo de caja. Los electrones están sujetos a interacciones con otros electrones, y con los núcleos de los átomos, por lo que no es cierto que la energía potencial sea cero. A pesar de que la diferencia parece grande, no deberías estar demasiado decepcionado por el resultado. En realidad es bastante impresionante que un modelo tan simple pueda dar una predicción que no está tan lejos del resultado experimental. Hoy en día los químicos utilizan computadoras para analizar modelos más sofisticados que no se pueden resolver analíticamente en la forma en que acabamos de resolver la partícula en la caja. Sin embargo, hay algunos aspectos cualitativos de la partícula en el modelo de caja que son útiles a pesar de las aproximaciones. Uno de estos aspectos es que la longitud de onda de la luz absorbida disminuye a medida que reducimos el tamaño de la caja. De la Ecuación\ ref {eqn2}, podemos escribir:
\[h c/\lambda=\left(\frac{\pi}{L}\right)^2\frac{\hbar^2}{2m}(n_2^2-n_1^2) \nonumber\]
donde\(n_2\) es el nivel desocupado más bajo, y\(n_1\) es el nivel ocupado más alto. Porque\(n_2=n_1+1\),
\[h c/\lambda=\left(\frac{\pi}{L}\right)^2\frac{\hbar^2}{2m}((n_1+1)^2-n_1^2)=\left(\frac{\pi}{L}\right)^2\frac{\hbar^2}{2m}(2n_1+1) \nonumber\]
Las moléculas que tienen un sistema conjugado más largo absorberán luz de longitudes de onda más largas (menos energía), y las moléculas con un sistema conjugado más corto absorberán luz de longitudes de onda más cortas (mayor energía). Por ejemplo, considere la siguiente molécula, que es miembro de una familia de tintes fluorescentes conocidos como cianinas. El sistema conjugado contiene 8\(\pi\) electrones, y la molécula absorbe luz de alrededor de 550 nm. Esta longitud de onda corresponde a la región verde del espectro visible. La solución absorbe el verde y deja que todo lo demás llegue a tu ojo. El rojo es el color complementario del verde, por lo que esta molécula en solución se verá roja para ti.

Ahora mira esta otra cianina, que tiene dos\(\pi\) electrones extra:
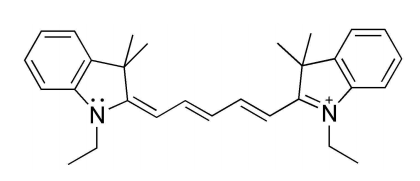
El modelo de partícula en una caja te dice que esta cianina debe absorber luz de longitudes de onda más largas (menos energía), por lo que no debería sorprenderte saber que una solución de este compuesto absorbe luz de aproximadamente 670 nm. Esto corresponde a la región naranja-roja del espectro, y la solución nos verá azul. Si en cambio acortamos la cadena conjugada produciremos un compuesto que absorbe en el azul (450 nm), y que será amarillo cuando esté en solución. Acabamos de conectar ecuaciones diferenciales, mecánica cuántica y los colores de las cosas... ¡impresionante!

