10.1: Sistemas de coordenadas
- Page ID
- 69805
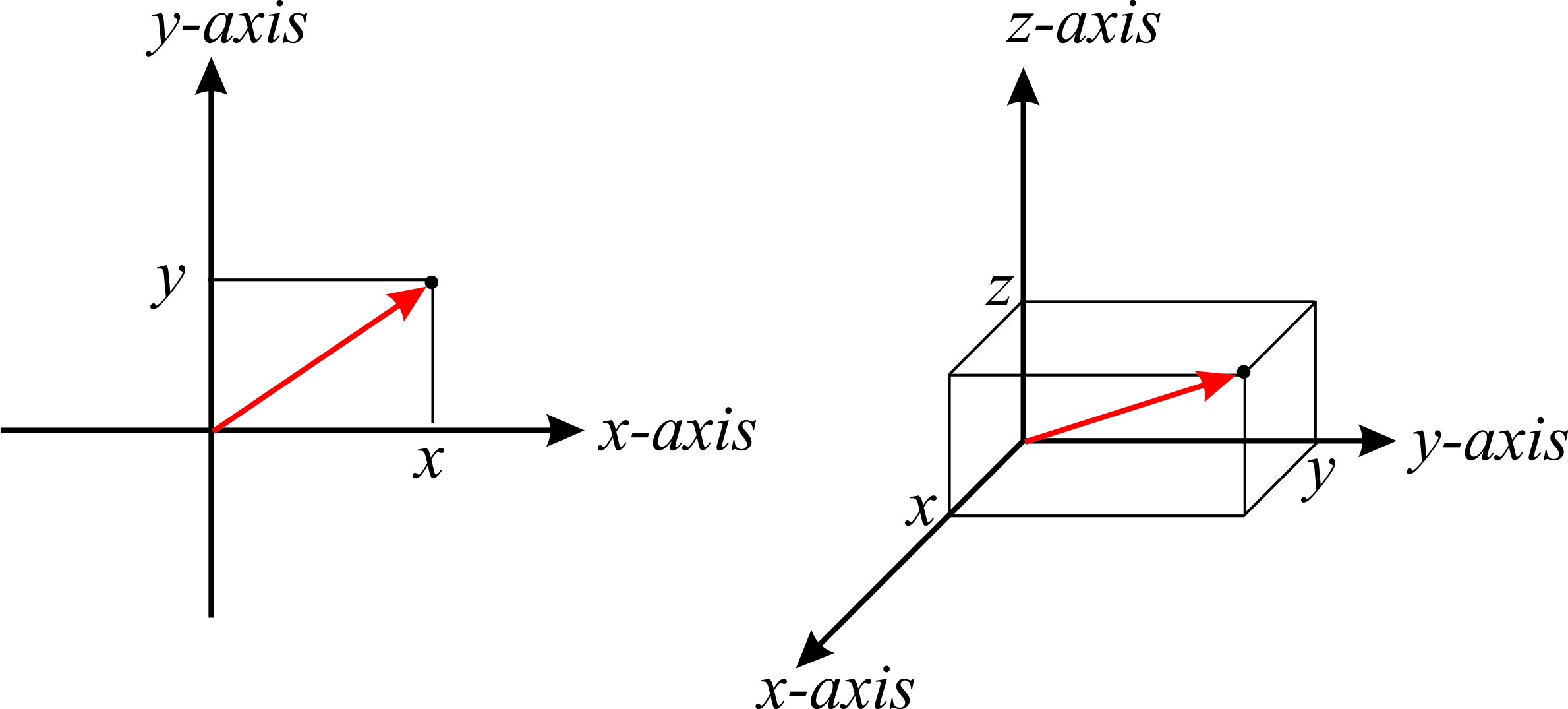
El sistema de coordenadas más simple consiste en ejes de coordenadas orientados perpendicularmente entre sí. Estas coordenadas se conocen como coordenadas cartesianas o coordenadas rectangulares, y ya estás familiarizado con su representación bidimensional y tridimensional. En el plano, cualquier punto\(P\) puede ser representado por dos números con signo, generalmente escritos como\((x,y)\), donde la coordenada\(x\) es la distancia perpendicular al\(x\) eje, y la coordenada\(y\) es la distancia perpendicular al\(y\) eje (Figura\(\PageIndex{1}\), izquierda). En el espacio, un punto está representado por tres números firmados, generalmente escritos como\((x,y,z)\) (Figura\(\PageIndex{1}\), derecha).
A menudo, las posiciones están representadas por un vector\(\vec{r}\), que se muestra en rojo en la Figura\(\PageIndex{1}\). En tres dimensiones, este vector se puede expresar en términos de los valores de coordenadas como\(\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}\), dónde\(\hat{i}=(1,0,0)\),\(\hat{j}=(0,1,0)\) y\(\hat{z}=(0,0,1)\) son los llamados vectores unitarios.
Ya sabemos que muchas veces la simetría de un problema lo hace natural (¡y más fácil!) para utilizar otros sistemas de coordenadas. En dos dimensiones, el sistema de coordenadas polares define un punto en el plano por dos números: la distancia\(r\) al origen, y el ángulo\(\theta\) que forma el vector de posición con el\(x\) eje -eje. Observe la diferencia entre\(\vec{r}\), un vector, y\(r\), la distancia al origen (y por lo tanto el módulo del vector). Los vectores a menudo se denotan en negrita (e.g. r) sin la flecha en la parte superior, así que tenga cuidado de no confundirlo con\(r\), que es un escalar.
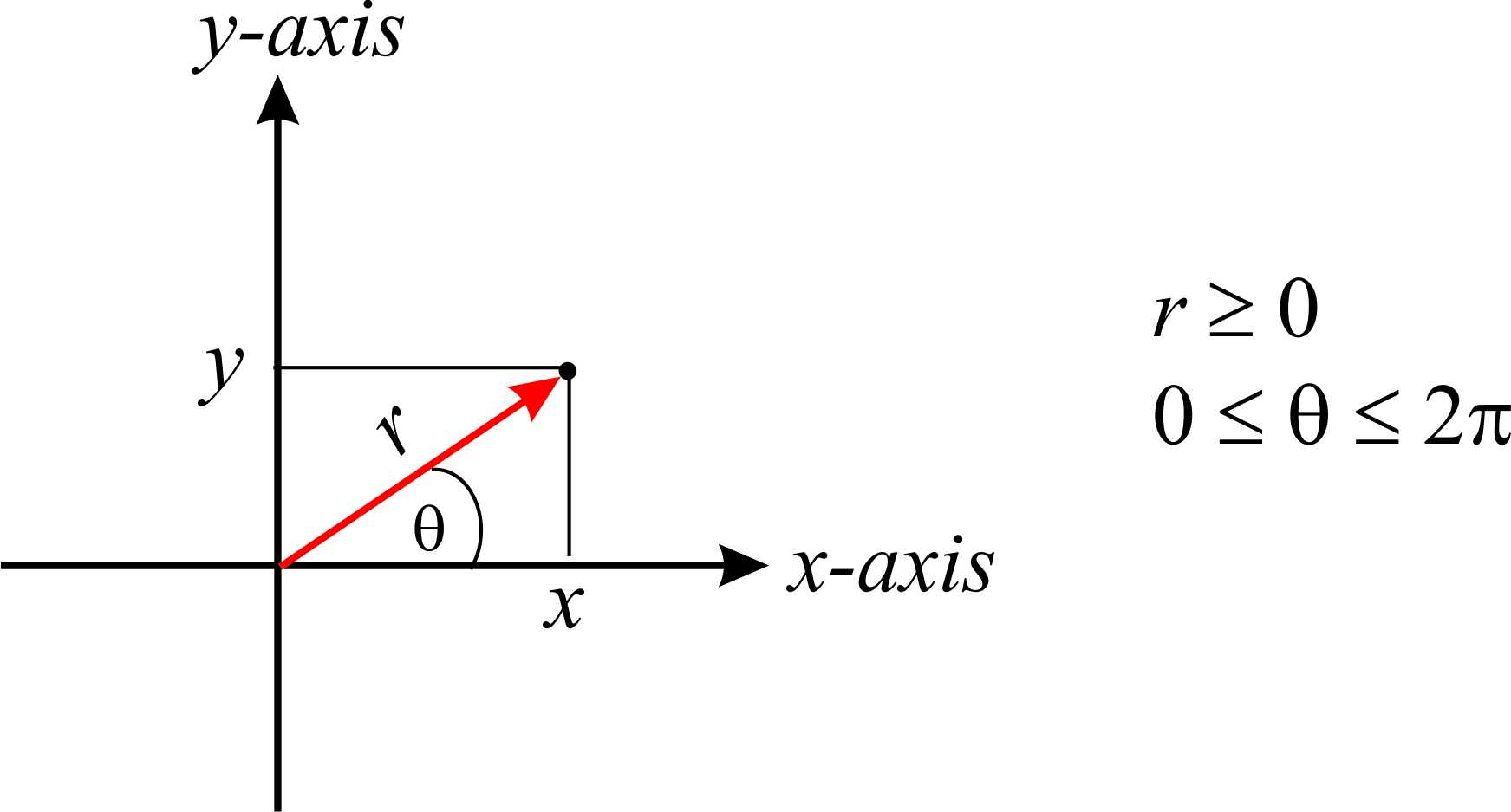
Mientras que en coordenadas cartesianas\(x\),\(y\) (y\(z\) en tres dimensiones) puede tomar valores de\(-\infty\) a\(\infty\), en coordenadas polares\(r\) es un valor positivo (consistente con una distancia), y\(\theta\) puede tomar valores en el rango\([0,2\pi]\).
La relación entre las coordenadas cartesianas y polares en dos dimensiones puede resumirse como:
\[\label{eq:coordinates_1} x=r\cos\theta\]
\[\label{eq:coordinates_2} y=r\sin\theta\]
\[\label{eq:coordinates_3} r^2=x^2+y^2\]
\[\label{eq:coordinates_4} \tan \theta=y/x\]
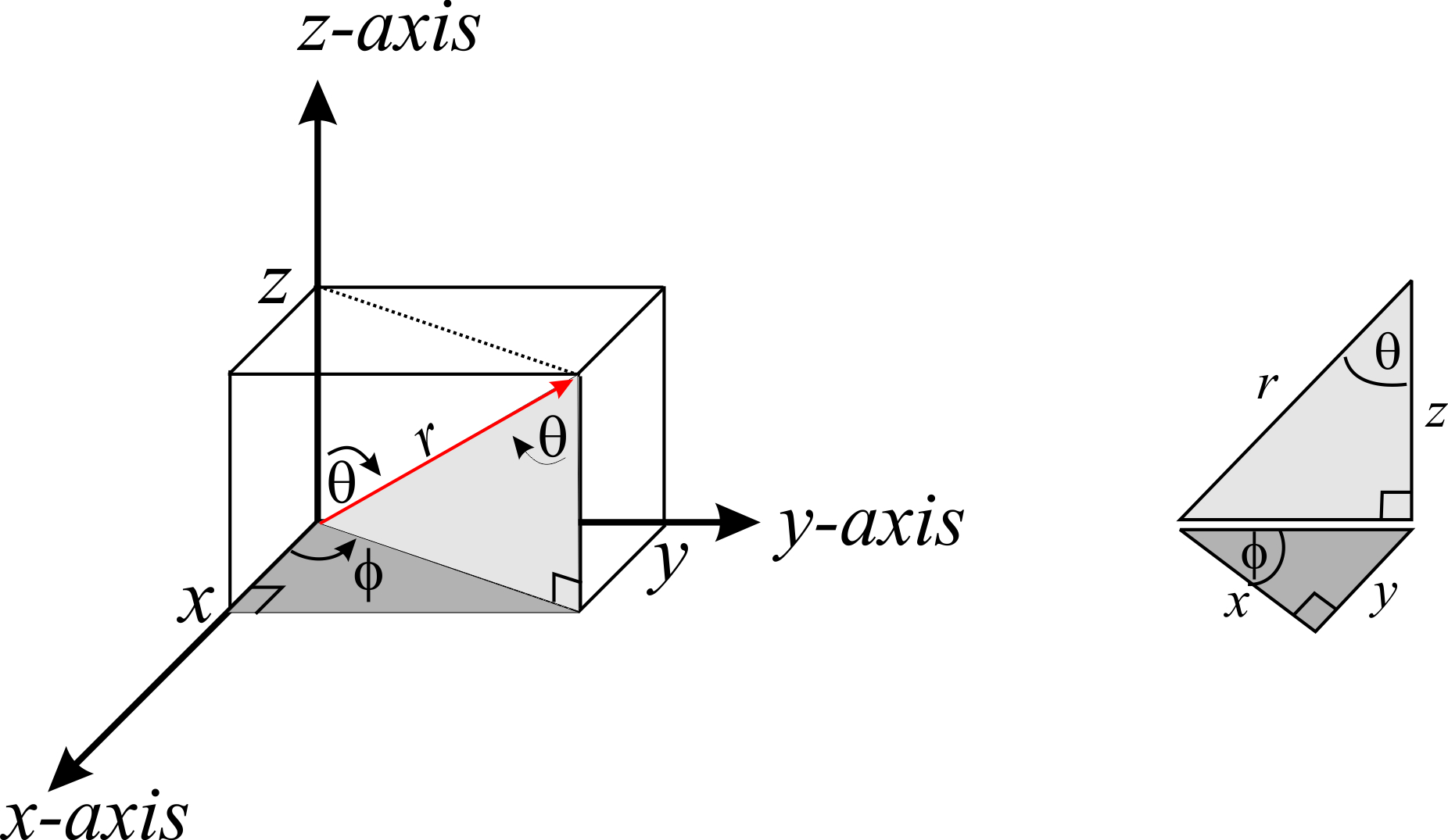
En tres dimensiones, el sistema de coordenadas esféricas define un punto en el espacio por tres números: la distancia\(r\) al origen, un ángulo polar\(\phi\) que mide el ángulo entre el\(x\) eje positivo y la línea desde el origen hasta el punto\(P\) proyectado sobre el\(xy\) plano , y el ángulo\(\theta\) definido como el es el ángulo entre el\(z\) eje y la línea desde el origen hasta el punto\(P\):
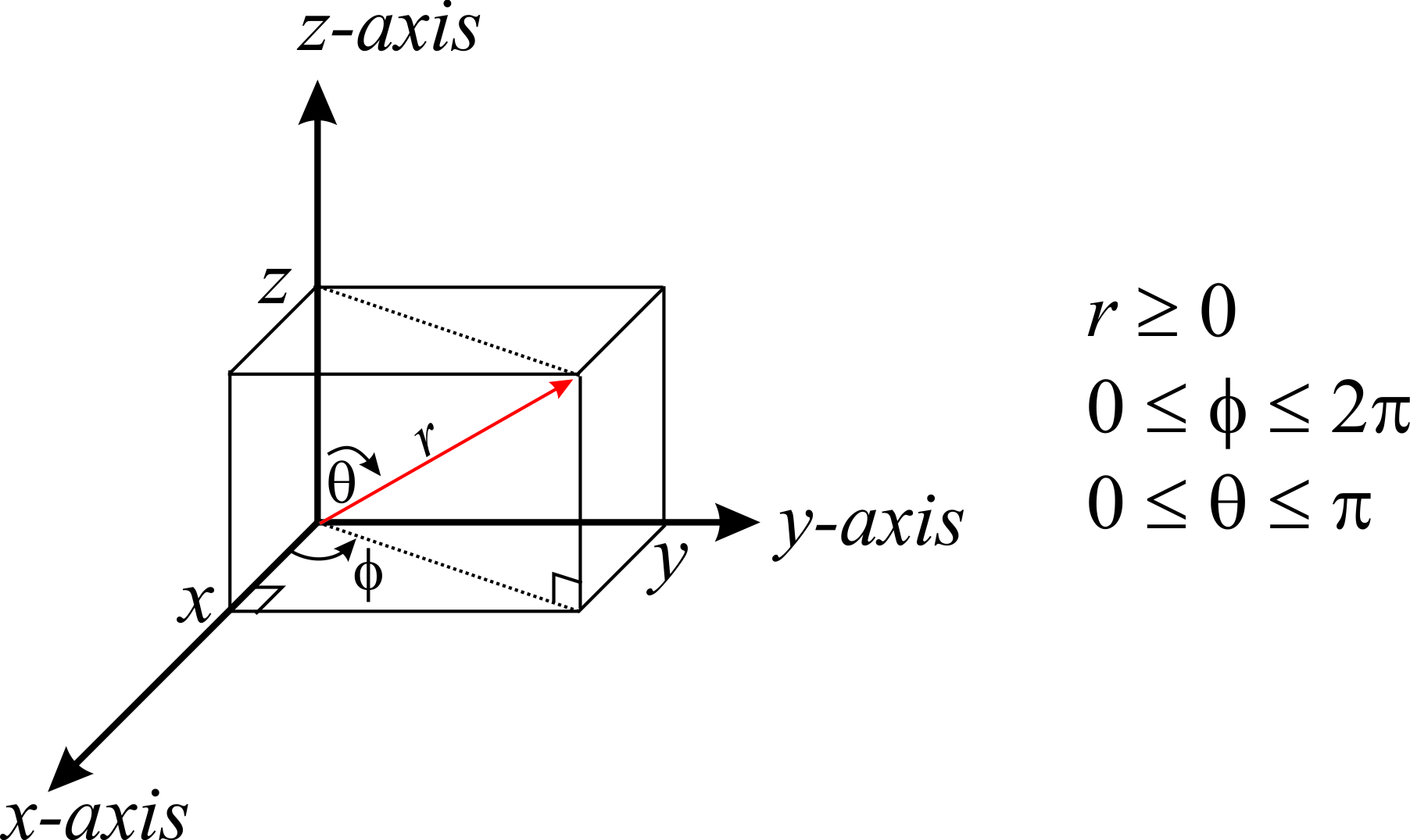
Antes de seguir adelante, es importante mencionar que dependiendo del campo, es posible que veas la letra griega\(\theta\) (en lugar de\(\phi\)) utilizada para el ángulo entre el\(x\) eje positivo y la línea desde el origen hasta el punto\(P\) proyectado sobre el\(xy\) plano. Es decir,\(\theta\) y\(\phi\) puede parecer intercambiado. Esto puede ser muy confuso, así que tendrás que tener cuidado. Al usar coordenadas esféricas, es importante que veas cómo se definen estos dos ángulos para que puedas identificar cuál es cuál.
Las coordenadas esféricas son útiles para analizar sistemas que son simétricos alrededor de un punto. Por ejemplo una esfera que tiene la ecuación cartesiana\(x^2+y^2+z^2=R^2\) tiene la ecuación muy simple\(r = R\) en coordenadas esféricas. Las coordenadas esféricas son las coordenadas naturales para situaciones físicas donde hay simetría esférica (por ejemplo, átomos). La relación entre las coordenadas cartesianas y las coordenadas esféricas se puede resumir como:
\[\label{eq:coordinates_5} x=r\sin\theta\cos\phi\]
\[\label{eq:coordinates_6} y=r\sin\theta\sin\phi\]
\[\label{eq:coordinates_7} z=r\cos\theta\]
Estas relaciones no son difíciles de derivar si se consideran los triángulos mostrados en la Figura\(\PageIndex{4}\):