10.2: Elementos de área y volumen

En cualquier sistema de coordenadas es útil definir un área diferencial y un elemento de volumen diferencial. En las coordenadas cartesianas el elemento de área diferencial es simplemente\(dA=dx\;dy\) (Figura\(\PageIndex{1}\)), y el elemento volumen es simplemente\(dV=dx\;dy\;dz\).

Figura\(\PageIndex{1}\): Elementos de área y volumen en coordenadas cartesianas (CC BY-NC-SA; Marcia Levitus)

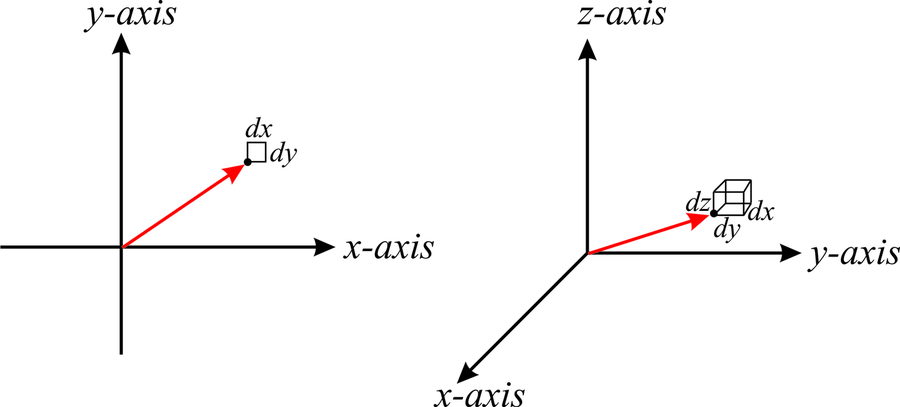
Ya realizamos integrales dobles y triples en coordenadas cartesianas, y utilizamos los elementos de área y volumen sin prestar especial atención. Por ejemplo, en el ejemplo [c2v:c2vex1], se nos requería integrar la función\({\left | \psi (x,y,z) \right |}^2\) sobre todo el espacio, y sin pensar demasiado usamos el elemento volume\(dx\;dy\;dz\) (ver página). También sabíamos que “todo el espacio” significaba\(-\infty\leq x\leq \infty\),\(-\infty\leq y\leq \infty\) y\(-\infty\leq z\leq \infty\), y por lo tanto escribimos:

\[\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }{\left | \psi (x,y,z) \right |}^2\; dx \;dy \;dz=1 \nonumber\]

Pero, ¿y si tuviéramos que integrar una función que se expresa en coordenadas esféricas? ¿Simplemente reemplazaríamos\(dx\;dy\;dz\) por\(dr\; d\theta\; d\phi\)? La respuesta es no, porque el elemento de volumen en coordenadas esféricas depende también de la posición real del punto. Esto tendrá más sentido en un minuto. Volviendo a las coordenadas en dos dimensiones, es intuitivo entender por qué el elemento area en coordenadas cartesianas es\(dA=dx\;dy\) independiente de los valores de\(x\) y\(y\). Esto se muestra en el lado izquierdo de la Figura\(\PageIndex{2}\). Sin embargo, en coordenadas polares, vemos que las áreas de las secciones grises, que se construyen\(r\) al aumentar en\(dr\), y\(\theta\) al aumentar en\(d\theta\), dependen del valor real de\(r\). Observe que el área resaltada en gris aumenta a medida que nos alejamos del origen.

Figura\(\PageIndex{2}\): Diferencial de área en coordenadas cartesianas y polares (CC BY-NC-SA; Marcia Levitus)

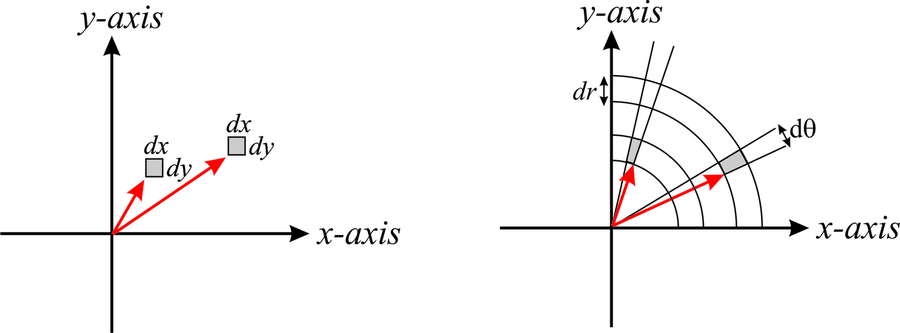
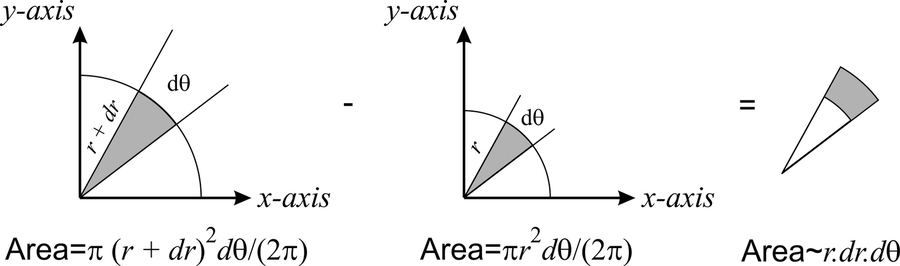
El área que se muestra en gris se puede calcular a partir de argumentos geométricos como

\[dA=\left[\pi (r+dr)^2- \pi r^2\right]\dfrac{d\theta}{2\pi}.\]

Porque\(dr<<0\), podemos descuidar el término\((dr)^2\), y\(dA= r\; dr\;d\theta\) (ver Figura\(10.2.3\)).

Figura\(\PageIndex{3}\): Diferencial de área en coordenadas polares (CC BY-NC-SA; Marcia Levitus)

Veamos cómo afecta esto a una doble integral con un ejemplo de la mecánica cuántica. La función de onda del estado fundamental de un oscilador armónico bidimensional es:\(\psi(x,y)=A e^{-a(x^2+y^2)}\). Sabemos que la cantidad\(|\psi|^2\) representa una densidad de probabilidad, y como tal, necesita normalizarse:

\[\int\limits_{all\;space} |\psi|^2\;dA=1 \nonumber\]

Esta afirmación es verdadera independientemente de si la función se expresa en coordenadas polares o cartesianas. Sin embargo, los límites de integración y la expresión utilizada para\(dA\), dependerán del sistema de coordenadas utilizado en la integración.

En coordenadas cartesianas, “todo el espacio” significa\(-\infty<x<\infty\) y\(-\infty<y<\infty\). El diferencial de área es\(dA=dxdy\):

\[\int\limits_{all\;space} |\psi|^2\;dA=\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty} A^2e^{-2a(x^2+y^2)}\;dxdy=1 \nonumber\]

En coordenadas polares, “todo el espacio” significa\(0<r<\infty\) y\(0<\theta<2\pi\). El diferencial de área es\(dA=r\;drd\theta\). La función se\(\psi(x,y)=A e^{-a(x^2+y^2)}\) puede expresar en coordenadas polares como:\(\psi(r,\theta)=A e^{-ar^2}\)

\[\int\limits_{all\;space} |\psi|^2\;dA=\int\limits_{0}^{\infty}\int\limits_{0}^{2\pi} A^2 e^{-2ar^2}r\;d\theta dr=1 \nonumber\]

Ambas versiones de la doble integral son equivalentes, y ambas pueden resolverse para encontrar el valor de la constante de normalización (\(A\)) que hace que la doble integral sea igual a 1. En coordenadas polares:

\[\int\limits_{0}^{\infty}\int\limits_{0}^{2\pi} A^2 e^{-2ar^2}r\;d\theta dr=A^2\int\limits_{0}^{\infty}e^{-2ar^2}r\;dr\int\limits_{0}^{2\pi}\;d\theta =A^2\times\dfrac{1}{4a}\times2\pi=1 \nonumber\]

Por lo tanto ¹,\(A=\sqrt{2a/\pi}\). El mismo valor se obtiene por supuesto integrando en coordenadas cartesianas.

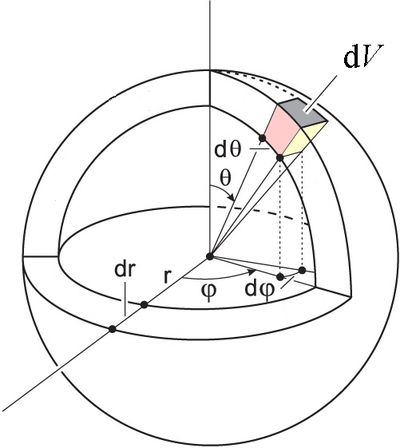
Ahora es el momento de dirigir nuestra atención a las integrales triples en coordenadas esféricas. En las coordenadas cartesianas, el elemento de volumen diferencial es simplemente\(dV= dx\,dy\,dz\), independientemente de los valores de\(x, y\) y\(z\). Usando los mismos argumentos que usamos para las coordenadas polares en el plano, veremos que el diferencial de volumen en coordenadas esféricas no lo es\(dV=dr\,d\theta\,d\phi\). La derivación geométrica del volumen es un poco más complicada, pero a partir de Figura\(\PageIndex{4}\) deberías poder ver que\(dV\) depende de\(r\) y\(\theta\), pero no de\(\phi\). El volumen de la región sombreada es

\[\label{eq:dv} dV=r^2\sin\theta\,d\theta\,d\phi\,dr\]

Figura\(\PageIndex{4}\): Diferencial de volumen en coordenadas esféricas (CC BY-NC-SA; Marcia Levitus)

Ejemplificaremos el uso de triples integrales en coordenadas esféricas con algunos problemas de la mecánica cuántica. Ya introdujimos la ecuación de Schrödinger, e incluso la resolvimos para un sistema simple en la Sección 5.4. También mencionamos que las coordenadas esféricas son la opción obvia al escribir esta y otras ecuaciones para sistemas como los átomos, que son simétricos alrededor de un punto.

Como vimos en el caso de la partícula en la caja (Sección 5.4), la solución de la ecuación de Schrödinger tiene una constante multiplicativa arbitraria. Debido a la interpretación probabilística de las funciones de onda, determinamos esta constante por normalización. La misma situación surge en tres dimensiones cuando resolvemos la ecuación de Schrödinger para obtener las expresiones que describen los posibles estados del electrón en el átomo de hidrógeno (es decir, los orbitales del átomo). La ecuación de Schrödinger es una ecuación diferencial parcial en tres dimensiones, y las soluciones serán funciones de onda que son funciones de\(r, \theta\) y\(\phi\). El estado energético más bajo, que en química llamamos orbital 1s, resulta ser:

\[\psi_{1s}=Ae^{-r/a_0} \nonumber\]

Este orbital en particular depende\(r\) únicamente, lo que no debería sorprender a un químico dado que la densidad electrónica en todos los\(s\) orbitales es esféricamente simétrica. Eso lo veremos\(p\) y\(d\) los orbitales dependen también de los ángulos. Independientemente de la órbita y del sistema de coordenadas, la condición de normalización establece que:

\[\int\limits_{all\;space} |\psi|^2\;dV=1 \nonumber\]

Para una función de onda expresada en coordenadas cartesianas,

\[\int\limits_{all\;space} |\psi|^2\;dV=\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\psi^*(x,y,z)\psi(x,y,z)\,dxdydz \nonumber\]

donde usamos el hecho de que\(|\psi|^2=\psi^* \psi\).

En coordenadas esféricas, “todo el espacio” significa\(0\leq r\leq \infty\),\(0\leq \phi\leq 2\pi\) y\(0\leq \theta\leq \pi\). El diferencial\(dV\) es\(dV=r^2\sin\theta\,d\theta\,d\phi\,dr\), entonces

\[\int\limits_{all\;space} |\psi|^2\;dV=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}\psi^*(r,\theta,\phi)\psi(r,\theta,\phi)\,r^2\sin\theta\,dr d\theta d\phi=1 \nonumber\]

Veamos cómo podemos normalizar orbitales usando triples integrales en coordenadas esféricas.

Ejemplo\(\PageIndex{1}\)

Al resolver la ecuación de Schrödinger para el átomo de hidrógeno\(\psi_{1s}=Ae^{-r/a_0}\), obtenemos, donde\(A\) es una constante arbitraria que necesita ser determinada por normalización. Encuentra\(A\).

Solución

En coordenadas esféricas,

\[\int\limits_{all\; space} |\psi|^2\;dV=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}\psi^*(r,\theta,\phi)\psi(r,\theta,\phi)\,r^2\sin\theta\,dr d\theta d\phi=1 \nonumber\]

porque este orbital es una función real,\(\psi^*(r,\theta,\phi)\psi(r,\theta,\phi)=\psi^2(r,\theta,\phi)\). En este caso,\(\psi^2(r,\theta,\phi)=A^2e^{-2r/a_0}\).

Por lo tanto,

\[\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}\psi^*(r,\theta,\phi)\psi(r,\theta,\phi) \, r^2 \sin\theta \, dr d\theta d\phi=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}A^2e^{-2r/a_0}\,r^2\sin\theta\,dr d\theta d\phi=1 \nonumber\]

\[\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}A^2e^{-2r/a_0}\,r^2\sin\theta\,dr d\theta d\phi=A^2\int\limits_{0}^{2\pi}d\phi\int\limits_{0}^{\pi}\sin\theta \;d\theta\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr \nonumber\]

El resultado es un producto de tres integrales en una variable:

\[\int\limits_{0}^{2\pi}d\phi=2\pi \nonumber\]

\[\int\limits_{0}^{\pi}\sin\theta \;d\theta=-\cos\theta|_{0}^{\pi}=2 \nonumber\]

\[\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr=? \nonumber\]

De la hoja de fórmulas:

\[\int_{0}^{\infty}x^ne^{-ax}dx=\dfrac{n!}{a^{n+1}}, \nonumber\]

donde\(a>0\) y\(n\) es un entero positivo.

En este caso,\(n=2\) y\(a=2/a_0\), así:

\[\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr=\dfrac{2!}{(2/a_0)^3}=\dfrac{2}{8/a_0^3}=\dfrac{a_0^3}{4} \nonumber\]

Juntando las tres piezas:

\[A^2\int\limits_{0}^{2\pi}d\phi\int\limits_{0}^{\pi}\sin\theta \;d\theta\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr=A^2\times2\pi\times2\times \dfrac{a_0^3}{4}=1 \nonumber\]

\[A^2\times \pi \times a_0^3=1\rightarrow A=\dfrac{1}{\sqrt{\pi a_0^3}} \nonumber\]

El orbital normalizado 1s es, por lo tanto:

\[\displaystyle{\color{Maroon}\dfrac{1}{\sqrt{\pi a_0^3}}e^{-r/a_0}} \nonumber\]