11.1: Definiciones

Operadores matemáticos

Un operador matemático es un símbolo que representa una operación o regla matemática que transforma un objeto (función, vector, etc) en otro objeto del mismo tipo. Por ejemplo, cuando el operador derivado\(d/dx\), también denotado por\(\hat{D}_x\), opera sobre una función\(f(x)\), el resultado es la función\(df/dx\).

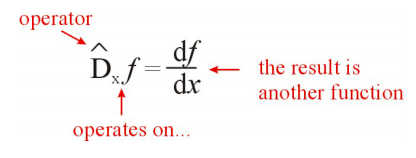
Podemos aplicar el operador\(\hat{D}_x\) a cualquier función. Por ejemplo, consideremos la función\(g(x) = 2 \cos x+e^x\):

\[\hat{D}_xg(x)=-2 \sin x + e^x \nonumber\]

En la química física, la mayoría de los operadores implican diferenciación o multiplicación. Por ejemplo, el operador de multiplicación denotado por\(\hat x\) medios “multiplicar por\(x\)”. Usando el ejemplo anterior, cuando\(\hat x\) opera en\(g(x)\) obtenemos

\[\hat{x}g(x)=2x \cos x +x e^x \nonumber\]

Antes de discutir para qué sirven los operadores, repasemos algunos ejemplos más. Primero, observe que denotamos operadores con un “sombrero”. Vamos a definir un operador\(\hat A\) (leer como “Un sombrero”) como\(\hat x + \dfrac{d}{dx}\)

\[\label{1} \hat A=\hat x + \dfrac{d}{dx}\]

Esto se lee como “multiplicar la función por\(x\) y agregar el resultado a la primera derivada de la función con respecto a\(x\)”. El segundo término es equivalente al operador que definimos antes\(\hat {D}_x\),, y usar uno u otro es cuestión de preferencia. Observe que la expresión\(\dfrac{d}{dx}\) no requiere un “sombrero” porque es inequívoca. En el caso de\(x\), necesitamos usar el “sombrero” para asegurarnos de distinguir el operador (multiplicar por\(x\)) de la variable\(x\). En el caso de\(\dfrac{d}{dx}\), la expresión claramente necesita ser aplicada a una función, por lo que obviamente es un operador. Cuando\(\hat A\) opera sobre la función\(g(x)\) (definida anteriormente), obtenemos:

\[\hat A g(x)=\hat x g(x) + \dfrac{d g}{dx}=-2 \sin x + e^x +2x \cos x +x e^x \nonumber\]

Operadores Lineales

En mecánica cuántica tratamos únicamente con operadores lineales. Se dice que un operador es lineal si

\[\hat A(c_1 f_1 (x)+c_2 f_2 (x))=\hat A c_1 f_1 (x)+\hat A c_2 f_2 (x) \nonumber\]

donde\(c_1\) y\(c_2\) son constantes (reales o complejas).

Por ejemplo, el\(\dfrac{d}{dx}\) operador es lineal:

\[\dfrac{d}{dx}(c_1 f_1 (x)+c_2 f_2 (x))= \dfrac{d}{dx} c_1 f_1 (x)+\dfrac{d}{dx} c_2 f_2 (x) \nonumber\]

Si definimos al operador\(\hat B\) como el operador “cuadrado” (tomar el cuadrado de...), notamos que no\(\hat B\) es lineal porque

\[\hat B(c_1 f_1 (x)+c_2 f_2 (x))=(c_1 f_1 (x))^2+(c_2 f_2 (x))^2+2c_1 f_1 (x)c_2 f_2 (x) \nonumber\]

que es claramente diferente de

\[\hat B(c_1 f_1 (x))+\hat B (c_2 f_2 (x))= (c_1 f_1 (x))^2+(c_2 f_2 (x))^2 \nonumber\]

Funciones propias y valores propios

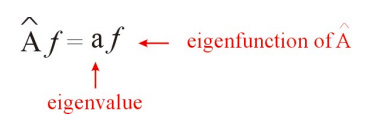
Un problema común en la mecánica cuántica es encontrar las funciones (\(f\)) y constantes (\(a\)) que satisfacen

\[\label{eigenfunction} \hat A f = a f\]

Discutiremos el significado físico de estas funciones y estas constantes más adelante. Por ahora, definiremos el concepto de función propia y valor propio de la siguiente manera:

Si el resultado de operar en una función es la misma función multiplicada por una constante, la función se denomina función propia de ese operador, y la constante de proporcionalidad se denomina valor propio.

Podemos probar si una función particular es una función propia de un operador dado o no. Por ejemplo, consideremos el operador\(-\dfrac{d^2}{dx^2}\) y la función\(g(x)\) definida en page. Es\(g(x)\) una función propia de\(-\dfrac{d^2}{dx^2}\)? En términos laicos: si tomamos la segunda derivada de\(g(x)\) y cambiamos el signo del resultado, ¿obtenemos una función que pueda expresarse como\(g(x)\) veces una constante?

Vamos a probarlo:

\[-\dfrac{d^2g(x)}{dx^2} = 2 \cos x - e^x \nonumber\]

El resultado no se puede expresar como un tiempo constante\(g(x)\):

\[2 \cos x - e^x \neq a(2 \cos x+ e^x) \nonumber\]

así que no\(g(x)\) es una función propia del operador\(-\dfrac{d^2}{dx^2}\).

Consideremos otra función:\(h(x) = 2sin(bx)\), donde\(b\) es una constante. ¿Es\(h(x)\) y función propia del operador\(-\dfrac{d^2}{dx^2}\)? Tomaremos la segunda derivada de\(g(x)\), multiplicaremos por\(-1\), y verificaremos si el resultado puede expresarse como un tiempo constante\(h(x)\):

\[-\dfrac{d^2h(x)}{dx^2} = 2b^2 \sin (bx) \nonumber\]

Observe que el resultado es\(b^2\) veces la función\(h(x)\), por lo que la conclusión\(h(x)\) es que es una función propia del operador\(-\dfrac{d^2}{dx^2}\), y que el valor propio correspondiente es\(b^2\). Un error común es concluir que el valor propio es\(2b^2\). Asegúrate de entender por qué esto está mal. . Además, observe que\(b^2\) es una constante porque no involucra a la variable\(x\). Otro error común es escribir valores propios que no sean constantes, sino que contengan la variable independiente.

Hasta ahora hemos aprendido a probar si una función dada es una función propia de un operador dado o no. ¿Cómo podemos calcular las funciones propias de un operador dado? En general, esto implica resolver una ecuación diferencial. Por ejemplo, las funciones propias del operador\(-\dfrac{d^2}{dx^2}\) satisfacen la ecuación

\[-\dfrac{d^2f(x)}{dx^2}=a f(x), \nonumber\]

donde\(a\) está el valor propio. Se trata de una ecuación diferencial ordinaria de segundo orden con coeficientes constantes, por lo que se puede resolver con los métodos que aprendimos en capítulos anteriores. ¿Puedes resolverlo y encontrar las funciones propias del operador\(-\dfrac{d^2}{dx^2}\)?

Las funciones propias y los valores propios de un operador juegan un papel central en la mecánica cuántica. Antes de continuar, presentaremos una propiedad importante que utilizará a menudo en su curso de química física:

Si dos funciones\(f_1(x)\) y\(f_2(x)\) son ambas funciones propias de un operador con el mismo valor propio, la combinación lineal también\(c_1f_1(x)+c_2f_2(x)\) será una función propia con el mismo valor propio.

Por ejemplo, las funciones\(e^{ax}\) y\(e^{-ax}\) son ambas funciones propias del operador\(\dfrac{d^2}{dx^2}\) con valor propio\(a^2\). Por lo tanto, cualquier combinación lineal\(c_1e^{ax}+c_2e^{-ax}\) será una función propia de este operador con valor propio\(a^2\), independientemente de los valores de\(c_1\) y\(c_2\). Para probarlo, tomar la segunda derivada de la función\(c_1e^{ax}+c_2e^{-ax}\) y demostrar que es igual a\(a^2\) veces\(c_1e^{ax}+c_2e^{-ax}\).

La función\(\cos(ax)\) es también una función propia de\(\dfrac{d^2}{dx^2}\). Sin embargo, la función no lo\(c_1e^{ax}+c_2\cos(ax)\) es. ¿Qué salió mal?