11.2: Álgebra de operador

Empecemos definiendo el operador de identidad, generalmente denotado por\(\hat E\) o\(\hat I\). El operador de identidad deja sin cambios el elemento sobre el que opera:\(\hat E f(x)=f(x)\). Esto es análogo a multiplicar por el número 1.

Podemos agregar operadores de la siguiente manera:

\[(\hat A + \hat B)f=\hat A f + \hat B f. \nonumber\]

Por ejemplo,

\[(\hat x + \dfrac{d}{dx})f = \hat x f + \dfrac{df}{dx}=x f + \dfrac{df}{dx} \nonumber\]

(recuerda que\(\hat x\) significa “multiplicar por\(x\)”).

El producto entre dos operadores se define como la operación sucesiva de los operadores, con el de la derecha operando primero. Por ejemplo,\((\hat x \dfrac{d}{dx})f=\hat x (\dfrac{df}{dx})=x \dfrac{df}{dx}\). Primero aplicamos el operador a la derecha (en este caso “toma la derivada de la función con respecto a\(x\)”), y luego el operador de la izquierda (“multiplica por\(x\) lo que tengas en el primer paso”). Podemos usar esta definición para calcular el cuadrado de un operador. Por ejemplo, si definimos al operador\(\hat A\) como\(\hat A = \dfrac{d}{dx}\), el operador\(\hat A^2\) es\(\hat A \hat A = \dfrac{d}{dx} \dfrac{d}{dx} =\dfrac{d^2}{dx^2}\).

La multiplicación por operadores no es, en general, conmutativa:\(\hat A \hat B \neq \hat B \hat A\). Es decir, en general, importa el orden de las operaciones. Antes, lo vimos\((\hat x \dfrac{d}{dx})f=x \dfrac{df}{dx}\). Volvamos el orden de la operación:\((\dfrac{d}{dx} \hat x )f\). Ahora, primero multiplicamos la función por\(x\) y luego tomamos la derivada del resultado:\((\dfrac{d}{dx} \hat x )f=\dfrac{d}{dx}(xf) =x \dfrac{df}{dx}+f\). En el último paso, calculamos la derivada del producto utilizando las reglas de diferenciación con las que estamos familiarizados.

Acabamos de demostrar que\(\hat x \dfrac{d}{dx} \neq \dfrac{d}{dx}\hat x\), o en otras palabras, el orden en que aplicamos estos dos operadores importa (es decir, si primero tomamos la derivada y luego multiplicamos por\(x\), o primero multiplicamos por\(x\) y luego tomamos la derivada). Si el orden importa o no tiene consecuencias muy importantes en la mecánica cuántica, por lo que es útil definir el llamado conmutador, definido como

\[\label{commutator} [\hat A,\hat B] = \hat A \hat B - \hat B \hat A.\]

Por ejemplo, el conmutador de los operadores\(\hat x\) y\(\dfrac{d}{dx}\), denotado por\([\hat x,\dfrac{d}{dx}]\), es por definición\(\hat x \dfrac{d}{dx} - \dfrac{d}{dx}\hat x\). Cuando\([\hat A,\hat B]=0\), los operadores\(\hat A\) y\(\hat B\) se dice que conmutan. Por lo tanto, si los operadores\(\hat A\) y\(\hat B\) conmutan, entonces\(\hat A \hat B = \hat B \hat A\). Cuando los operadores\(\hat A\) y\(\hat B\) no conmutan\(\hat A \hat B \neq \hat B \hat A\),, y el conmutador\([\hat A,\hat B]\neq 0\).

Antes de seguir adelante, es importante reconocer que el producto de dos operadores también es un operador. Por ejemplo, consideremos el producto\(\dfrac{d}{dx} \hat x\). Se trata de un operador que, cuando se aplica a una función\(f\), da una nueva función\(x \dfrac{df}{dx}+f\). Por ejemplo, si\(f= \sin (kx)\),\(\dfrac{d}{dx} \hat x f = kx \cos(kx) + \sin(kx)\). Además, observe que el operador\(\dfrac{d}{dx} \hat x\) puede expresarse como\(\hat E + \hat x \dfrac{d}{dx}\), donde\(\hat E\) está el operador de identidad. Cuando el operador\(\hat E + \hat x \dfrac{d}{dx}\) opera sobre una función\(f\), el resultado es la función misma (multiplicada por una) más\(x\) veces la derivada de la función, que es exactamente lo que obtenemos cuando realizamos\(\dfrac{d}{dx} \hat x f\).

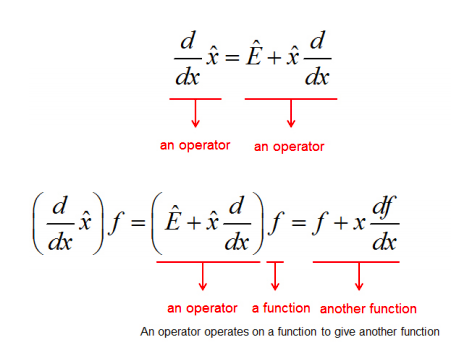
Del mismo modo, el conmutador entre dos operadores también es un operador:

Obsérvese que en el ejemplo del lado derecho de la figura demostramos que el operador\([\hat x,\dfrac{d}{dx}]\) es igual al operador\(-\hat E\) (“multiplicar por -1”). En otras palabras, cuando el conmutador\([\hat x,\dfrac{d}{dx}]\) (un operador) opera sobre una función\(f\), el resultado es\(-f\). Porque\([\hat x,\dfrac{d}{dx}] \neq 0\), los operadores\(\hat x\) y\(\dfrac{d}{dx}\) no conmutan. Esto está directamente relacionado con el principio de incertidumbre, que (en su forma más simple) establece que cuanto más precisamente se determine la posición de alguna partícula, menos precisamente se puede conocer su impulso. Veremos en un momento la conexión entre esta declaración y el conmutador, y lo discutirás con mucho detalle en tus futuros cursos de química física.

Ejemplo\(\PageIndex{1}\)

Encuentra el conmutador

\[[\hat x^2, \dfrac{d^2}{dx^2}] \nonumber\]

Solución

Recuerda que el conmutador es un operador, por lo que tu respuesta también debe ser un operador (es decir, no debe contener una función). Para 'ver' lo que hace el conmutador (para que podamos escribir el operador equivalente), aplicamos una función arbitraria:

\[[\hat x^2, \dfrac{d^2}{dx^2}]f=\hat x^2 \dfrac{d^2}{dx^2}f-\dfrac{d^2}{dx^2}\hat x^2 f \nonumber\]

Recuerda que cuando tenemos expresiones como\(\dfrac{d^2}{dx^2}\hat x^2 f\) tenemos que ir de derecha a izquierda, es decir, primero multiplicamos por\(x^2\) y sólo entonces tomamos la segunda derivada.

\[\dfrac{d^2}{dx^2}\hat x^2 f =\dfrac{d^2(x^2f)}{dx^2}=\dfrac{d(2xf+x^2 \dfrac{df}{dx})}{dx}=2x\dfrac{df}{dx}+2f+x^2\dfrac{d^2f}{dx^2}+2x\dfrac{df}{dx}=4x\dfrac{df}{dx}+2f+x^2\dfrac{d^2f}{dx^2} \nonumber\]

\[[\hat x^2, \dfrac{d^2}{dx^2}]f=\displaystyle{\color{Blue}\hat x^2 \dfrac{d^2}{dx^2}f}-\displaystyle{\color{Green}\dfrac{d^2}{dx^2}\hat x^2 f}=\displaystyle{\color{Blue}x^2\dfrac{d^2f}{dx^2}}-\displaystyle{\color{Green}\left(4x\dfrac{df}{dx}+2f+x^2\dfrac{d^2f}{dx^2}\right)}=-4x\dfrac{df}{dx}-2f \nonumber\]

\[[\hat x^2, \dfrac{d^2}{dx^2}]= \displaystyle{\color{Maroon}-4\hat x \dfrac{d}{dx}-2\hat E} \nonumber\]

Nuevamente, tu resultado debe ser un operador, y por lo tanto no debe contener la función\(f\). Porque\([\hat x^2, \dfrac{d^2}{dx^2}] \neq 0\), los dos operadores no se desplazan.

Errores comunes:

• escribir el conmutador como\([\hat x^2, \dfrac{d^2}{dx^2}] =-4x\dfrac{df}{dx}-2f\)
• usar una función real (por ejemplo\(\sin x\)) en lugar de una función arbitraria\(f\)