13.2: Cálculo de un determinante 3 × 3

Existen varias técnicas para calcular determinantes, pero si este tema es nuevo para ti, expandirte a lo largo de la primera fila es la forma más fácil (aunque quizás no la más eficiente computacionalmente) de hacerlo.

Una matriz de\(\times\) 3 3 se calcula como:

\[\label{eq:determinants1} \begin{vmatrix} a_{11} &a_{12} & a_{13} \\ a_{21} &a_{22} &a_{23} \\ a_{31} &a_{32} &a_{33} \end{vmatrix}= a_{11}\begin{vmatrix} a_{22}&a_{23}\\ a_{32}&a_{33} \end{vmatrix}- a_{12}\begin{vmatrix} a_{21}&a_{23}\\ a_{31}&a_{33} \end{vmatrix}+ a_{13}\begin{vmatrix} a_{21}&a_{22}\\ a_{31}&a_{32} \end{vmatrix} \]

Observe que multiplicamos cada entrada en la primera fila por el determinante formado por lo que queda después de eliminar la fila y columna correspondientes. Además, fíjate que alternamos signos. Formalmente, el signo que corresponde a una entrada en particular\(a_{ij}\) es\((-1)^{i+j}\), pero si usamos el primer raw siempre comenzaremos con un “+” y alternaremos signos después. En la Figura se muestra un esquema del procedimiento\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un determinante\(\times\) 3 3 (CC BY-NC-SA; Marcia Levitus)

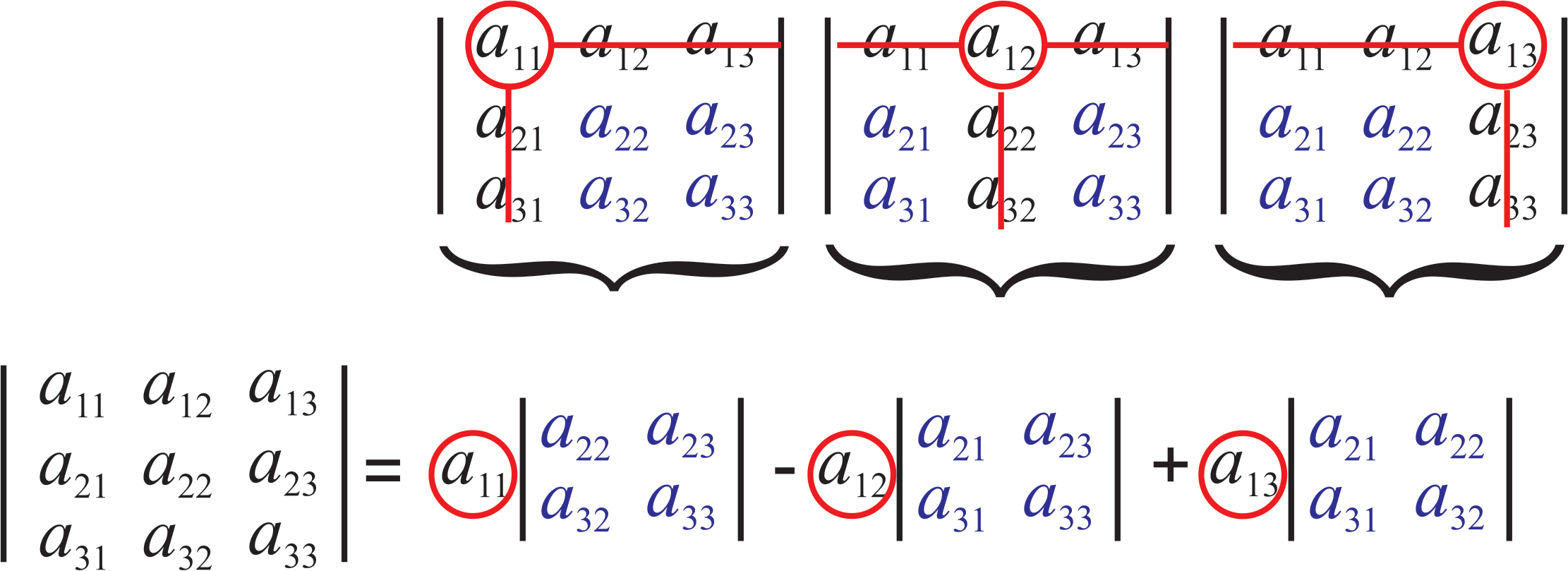
Podemos usar la misma idea para calcular un determinante de cualquier tamaño. Por ejemplo, para un\(4\times 4\) determinante:

\[\begin{vmatrix} a_{11} &a_{12} & a_{13} &a_{14}\\ a_{21} &a_{22} &a_{23} &a_{24}\\ a_{31} &a_{32} &a_{33} &a_{34}\\ a_{41} &a_{42} &a_{43} &a_{44}\\ \end{vmatrix}= a_{11}\begin{vmatrix} a_{22}&a_{23}&a_{24}\\ a_{32}&a_{33}&a_{34}\\ a_{42}&a_{43}&a_{44} \end{vmatrix}- a_{12}\begin{vmatrix} a_{21}&a_{23}&a_{24}\\ a_{31}&a_{33}&a_{34}\\ a_{41}&a_{43}&a_{44} \end{vmatrix}+ a_{13}\begin{vmatrix} a_{21}&a_{22}&a_{24}\\ a_{31}&a_{32}&a_{34}\\ a_{41}&a_{42}&a_{44} \end{vmatrix}- a_{14}\begin{vmatrix} a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\\ a_{41}&a_{42}&a_{43} \end{vmatrix} \label{4x4} \nonumber\]

\(3\times 3\)Los determinantes se calculan entonces usando la Ecuación\ ref {eq:determinantes1}.

Ejemplo\(\PageIndex{1}\)

Encuentra\(x\) en el siguiente sistema de ecuaciones:

\[\begin{align*}2x+3y+8z &=0 \\[4pt] x-\frac{1}{2}y-3z &=\frac{1}{2} \\ -x-y-z &=\frac{1}{2}\end{align*}\]

Solución

Podemos calcular el\(x\) as;

\[x=\frac{D_1}{D} \nonumber\]

donde

\[D=\begin{vmatrix} 2 &3 & 8 \\ 1 &-1/2 &-3 \\ -1 &-1 &-1 \end{vmatrix} \nonumber\]

y

\[D_1=\begin{vmatrix} 0 &3 & 8 \\ 1/2 &-1/2 &-3 \\ 1/2 &-1 &-1 \end{vmatrix} \nonumber\]

\(D\)es un determinante 3x3\(D\) y se puede expandir usando quation\ ref {eq:determinants1}:

\[ \begin{align*} D &= 2\begin{vmatrix} -1/2&-3\\ -1&-1 \end{vmatrix}- 3\begin{vmatrix} 1&-3\\ -1&-1 \end{vmatrix}+ 8\begin{vmatrix} 1&-1/2\\ -1&-1 \end{vmatrix} \\[4pt] &=2\times(-5/2)-(3)\times(-4)+8\times(-3/2)=-5 \end{align*}\]

El determinante\(D_1\) se expande de manera similar:

\[\begin{align*} D_1 &= 0\begin{vmatrix} -1/2&-3\\ -1&-1 \end{vmatrix}- 3\begin{vmatrix} 1/2&-3\\ 1/2&-1 \end{vmatrix} + 8\begin{vmatrix} 1/2&-1/2\\ 1/2&-1 \end{vmatrix} \\[4pt] &=0\times(-5/2)-(3)\times(1)+8\times(-1/4)=-5 \end{align*}\]

Entonces,

\[\displaystyle{\color{Maroon}x=\frac{D_1}{D}=1} \nonumber\]

Para practicar, terminar este problema y obtener\(y\) y\(z\) (Problema 13.1).

Ejemplo\(\PageIndex{2}\)

Mostrar que un\(3\times 3\) determinante que contiene ceros por debajo de la diagonal principal (superior izquierda a abajo derecha) es el producto de los elementos diagonales.

Solución

Se nos pide que probemos que

\[D=\begin{vmatrix} a &b&c \\ 0&d &e \\ 0& 0 &f \end{vmatrix}=adf \nonumber\]

Debido a que tenemos dos ceros en la primera columna, tiene más sentido calcular el determinante expandiéndose a lo largo de la primera columna en lugar de la primera fila. Sin embargo, si te sientes incómodo haciendo esto en este punto podemos expandirnos a lo largo de la primera fila como acabamos de aprender:

\[D=a\times\begin{vmatrix} d &e\\ 0&f\end{vmatrix}-b\times\begin{vmatrix} 0 &e\\ 0&f\end{vmatrix}+c\times\begin{vmatrix} 0 &d\\ 0&0\end{vmatrix}=a\times d\times f \nonumber\]

La conclusión es cierta en cualquier dimensión.

¿Necesitas ayuda? Los enlaces a continuación contienen ejemplos resueltos. El determinante de una matriz 3x3: http://tinyurl.com/n2a3uxw

Enlaces externos:

• Encontrar el determinante de una matriz 3x3: http://patrickjmt.com/finding-the-determinant-of-a-3-x-3-matrix/
• Resolviendo un sistema de 3 ecuaciones lineales: http://patrickjmt.com/cramers-rule-to-solve-a-system-of-3-linear-equations-example-1/