15.4: Operadores de simetría
- Page ID
- 70131
La simetría de las moléculas es esencial para comprender las estructuras y propiedades de los compuestos orgánicos e inorgánicos. Las propiedades de los compuestos químicos a menudo se explican fácilmente por la consideración de la simetría. Por ejemplo, la simetría de una molécula determina si la molécula tiene un momento dipolo permanente o no. Las teorías que describen la actividad óptica, la espectroscopia infrarroja y ultravioleta y la estructura cristalina implican la aplicación de consideraciones de simetría. El álgebra matricial es la herramienta matemática más importante en la descripción de la simetría.
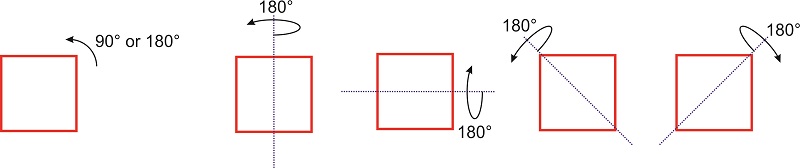
Una operación de simetría, como una rotación alrededor de un eje de simetría o una reflexión a través de un plano, es una operación que, cuando se realiza sobre un objeto, da como resultado una nueva orientación del objeto que es indistinguible del original. Por ejemplo, si giramos un cuadrado en el plano por\(\pi/2\) o\(\pi\) la nueva orientación del cuadrado es superpuesta sobre el original (Figura\(\PageIndex{1}\)).
Si la rotación por un ángulo\(\theta\) de una molécula (u objeto) alrededor de algún eje da como resultado una orientación de la molécula (u objeto) que se superpone sobre el original, el eje se denomina eje de rotación. Se dice que la molécula (u objeto) tiene un eje de rotación\(n\) -fold, donde\(n\) está\(2\pi/\theta\). El eje se denota como\(C_n\). El cuadrado de la Figura\(\PageIndex{1}\) tiene un\(C_4\) eje perpendicular al plano debido a que una\(90^{\circ}\) rotación deja la figura indistinguible de la orientación inicial. Este eje también es un\(C_2\) eje porque una rotación de\(180^{\circ}\) grados deja el cuadrado indistinguible del cuadrado original. Además, la figura tiene varios otros\(C_2\) ejes que se encuentran en el mismo plano que el cuadrado:
Una operación de simetría mueve todos los puntos del objeto de una posición inicial a una posición final, y eso significa que los operadores de simetría son matrices\(3\times 3\) cuadradas (o\(2\times 2\) en dos dimensiones). La siguiente ecuación representa la acción de un operador de simetría\(\hat A\) sobre la ubicación del punto\((x,y,z)\) (un vector):
\[\hat A (x,y,z)=(x',y',z') \nonumber\]
El vector\((x',y',z')\) representa la ubicación del punto después de la operación de simetría. Volvamos a los ejes de rotación que discutimos antes. Una rotación de 2 veces alrededor del\(z-\) eje cambia la ubicación de un punto\((x,y,z)\) a\((-x,-y,z)\) (ver Figura\(\PageIndex{2}\)). Por convención, las rotaciones siempre se toman en sentido contrario a las agujas del reloj.
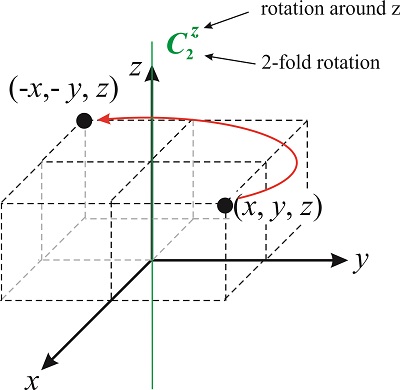
¿Cuál es la matriz que representa al operador\(\hat {C^z_2}\)? La matriz transforma el vector\((x,y,z)\) en\((-x,-y,z)\), entonces
\[\hat {C^z_2}(x,y,z)=(-x,-y,z) \nonumber\]
\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} -x \\ -y \\ z \end{pmatrix}\]
Sabemos que la matriz es una matriz\(3\times 3\) cuadrada porque necesita multiplicar un vector tridimensional. Además, escribimos el vector como columna vertical para satisfacer los requisitos de multiplicación matricial.
\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix} \nonumber\]
\[a_{11}x+a_{12}y+a_{13}z=-x \nonumber\]
\[a_{21}x+a_{22}y+a_{23}z=-y \nonumber\]
\[a_{31}x+a_{32}y+a_{33}z=z \nonumber\]
y concluimos que\(a_{11}=-1\)\(a_{12}=a_{13}=0\),\(a_{22}=-1\),\(a_{21}=a_{23}=0\) y\(a_{33}=1\),\(a_{31}=a_{32}=0\):
\[\hat{C^z_2}=\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber\]
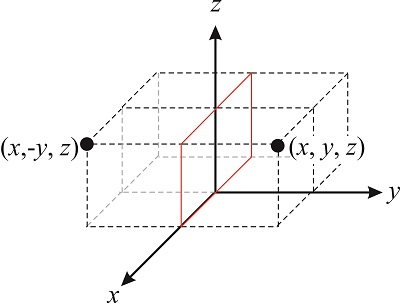
Las rotaciones no son las únicas operaciones de simetría que podemos realizar en una molécula. La figura\(\PageIndex{3}\) ilustra la reflexión de un punto a través del\(xz\) plano. Esta operación transforma el vector\((x,y,z)\) en el vector\((x,-y,z)\). Los operadores de simetría que involucran reflexiones a través de un plano generalmente se denotan con la letra\(\sigma\), por lo que el operador que refleja un punto a través del\(xz\) plano es\(\hat{\sigma}_{xz}\):
\[\hat{\sigma}_{xz}(x,y,z)=(x,-y,z) \nonumber\]
Siguiendo la misma lógica que usamos para la matriz de rotación, podemos escribir el\(\hat{\sigma}_{xz}\) operador como:
\[\hat{\sigma}_{x,z}=\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber\]
Esto es cierto porque
\[\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} x \\ -y \\ z \end{pmatrix} \nonumber\]
Como dijimos antes, las propiedades de simetría de las moléculas son esenciales para comprender las estructuras y propiedades de los compuestos orgánicos e inorgánicos. Por ejemplo, aquellos de ustedes que tomaron química orgánica saben que las moléculas que tienen un centro de inversión (Problema 15.3) no tienen momentos dipolares permanentes. La simetría de las moléculas también está relacionada con sus capacidades para absorber la luz. La figura\(\PageIndex{4}\) muestra los tres elementos de simetría de la molécula de agua (H\(_2\) O). Esta molécula tiene sólo un eje de rotación, que es de 2 veces, y por lo tanto la llamamos un “\(C_2\)eje”. También tiene dos planos espejo, uno que contiene los dos átomos de hidrógeno (\(\sigma_{yz}\)), y otro perpendicular a él (\(\sigma_{xz}\)). Ambos planos contienen el\(_2\) eje C.
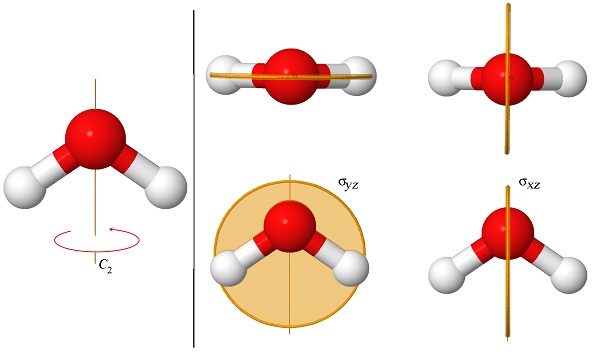
Como aprenderás en tu curso de química inorgánica, los químicos organizan moléculas que comparten los mismos elementos de simetría bajo un grupo común. Por ejemplo, al grupo que contiene moléculas con estos tres elementos de simetría se le llama “el\(C_{2v}\) grupo”. Debido a que la operación de inversión (Problema 15.3) no forma parte de este grupo sabemos que todas las\(C_{2v}\) moléculas son polares.
La molécula de metano (CH\(_4\)) tiene varios elementos de simetría, algunos de los cuales no hemos aprendido en este capítulo. Uno que es relativamente fácil de identificar es el eje de\(_3\) rotación C (Figura\(\PageIndex{5}\)):
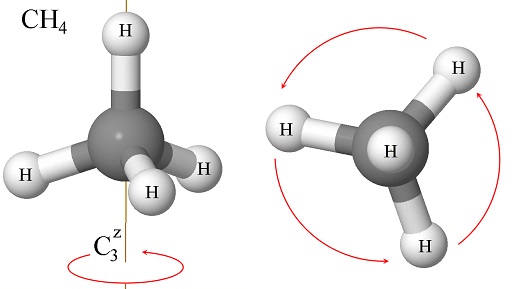
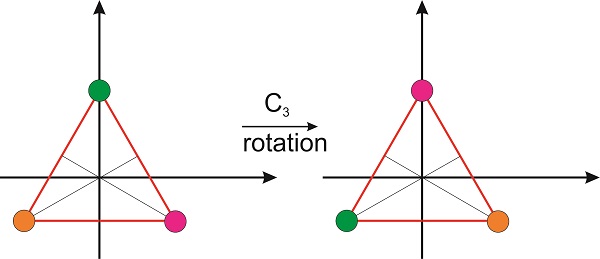
¿Podemos escribir la matriz para el operador que corresponda a la rotación de 3 veces? Si miramos la molécula desde arriba, entonces el\(z\) eje -es perpendicular al plano del papel (o pantalla si estás leyendo esto en una computadora), vemos que la rotación mueve un átomo de hidrógeno de un vértice de un triángulo equilátero al otro en sentido antihorario. Por lo tanto, necesitamos una matriz que mueva estos vértices como se muestra en la figura:
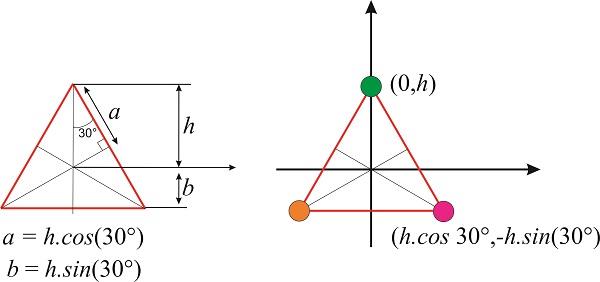
Necesitamos las coordenadas de los tres vértices, que se pueden obtener a partir de simples argumentos geométricos. Si colocamos el vértice verde en\(x=0\) y\(y=h\), entonces la posición del vértice magenta es\(x=h\times \cos 30^{\circ}\) y\(y=-h\times \sin 30^{\circ}\) y la posición del vértice naranja es\(-x=h\times \cos 30^{\circ}\) y\(y=-h\times \sin 30^{\circ}\) (Figura\(\PageIndex{7}\)).
La matriz que estamos buscando necesita rotar el círculo magenta hasta que se superponga con el círculo verde:
\[\hat {C}_3(h \sqrt{3}/2,-h/2,z)=(0,h,z) \nonumber\]
donde observamos que esta rotación no cambia el valor de\(z\).
\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} h\sqrt{3}/2 \\ -h/2\\ z\end{pmatrix}=\begin{pmatrix} 0 \\ h \\ z \end{pmatrix} \nonumber\]
Aquí, hemos utilizado el hecho de que\(\cos30^{\circ}=\sqrt{3}/2\) y\(\sin 30^{\circ}=1/2\).
Multiplicando la matriz por el vector:
\[a_{11}h\sqrt{3}/2-a_{12}h/2+a_{13}z=0 \nonumber\]
\[a_{21}h\sqrt{3}/2-a_{22}h/2+a_{23}z=h \nonumber\]
\[a_{31}h\sqrt{3}/2-a_{32}h/2+a_{33}z=z \nonumber\]
A partir de estas ecuaciones, concluimos que\(a_{13}=a_{23}=a_{31}=a_{32}=0\),\(a_{12}=\sqrt{3}a_{11}\), y\(a_{22}=\sqrt{3}a_{21}-2\). Hasta ahora la matriz se ve así:
\[\hat {C}_3=\begin{pmatrix} a_{11}&\sqrt{3}a_{11}&0 \\ a_{21}&\sqrt{3}a_{21}-2&0 \\ 0&0&1 \end{pmatrix} \nonumber\]
Para encontrar las entradas restantes vamos a aplicar la matriz al vector\((0,h,z)\), que necesita rotar para\((-h \sqrt{3}/2,-h/2,z)\):
\[\begin{pmatrix} a_{11}&\sqrt{3}a_{11}&0 \\ a_{21}&\sqrt{3}a_{21}-2&0 \\ 0&0&1 \end{pmatrix}\begin{pmatrix} 0 \\ h \\ z \end{pmatrix}=\begin{pmatrix} -h \sqrt{3}/2 \\ -h/2 \\ z \end{pmatrix} \nonumber\]
De esta multiplicación obtenemos
\[\sqrt{3}a_{11}h=-h\sqrt{3}/2\rightarrow a_{11}=-1/2 \nonumber\]
\[(\sqrt{3}a_{21}-2)h=-h/2\rightarrow a_{21}=\sqrt{3}/2 \nonumber\]
y por lo tanto,
\[\hat {C}_3=\begin{pmatrix} -1/2&-\sqrt{3}/2&0 \\ \sqrt{3}/2&-1/2&0 \\ 0&0&1 \end{pmatrix} \nonumber\]

