4.6: Ley de Boyle desde la Densidad de Probabilidad Maxwell-Boltzmann

En el capítulo 2, derivamos la ley de Boyle La ley de Boyle utilizando suposiciones simplificadoras. Ahora estamos en condiciones de hacer esta derivación mucho más rigurosamente. Consideramos las colisiones de moléculas de gas con una pequeña porción de la pared de su contenedor. Suponemos que el muro es liso, para que podamos seleccionar un segmento pequeño y compacto del mismo que esté arbitrariamente cerca de ser plano. Denotamos tanto el segmento del muro como su área como\(A\). \(A\)puede tener cualquier forma siempre que sea una superficie lisa y plana encerrada por una curva suave.

Deje que el volumen del contenedor sea\(V\) y el número de moléculas de gas en el recipiente sea\(N\). Imaginamos que seguimos la trayectoria de una molécula en particular a medida que se mueve para golpear la pared en algún lugar dentro\(A\). Comenzamos nuestras observaciones en el momento\(t=0\) y suponemos que la colisión ocurre en el momento\(t\).

Figura 3. Trayectoria de una molécula colisionando con una pared de su contenedor.

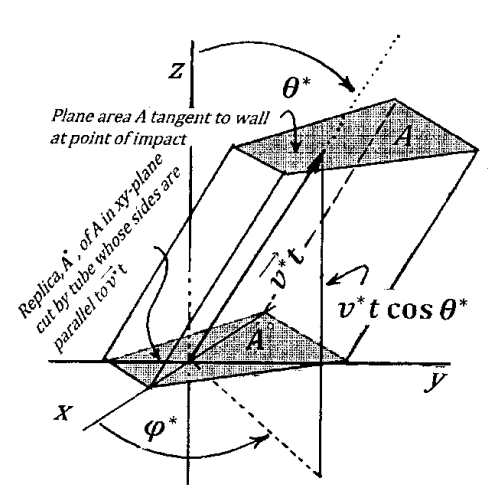
Como se esboza en la Figura 3, erigimos un sistema de coordenadas cartesianas con su origen en la ubicación en el espacio de la molécula en el tiempo\(t=0\). Orientamos los ejes de este sistema de coordenadas para que el\(xy\) plano -sea paralelo al plano de\(A\), y el eje z apunte hacia la pared. Entonces el vector unitario a lo largo del\(z\) eje -y un vector perpendicular a\(A\) son paralelos entre sí. Es conveniente expresar la velocidad de la molécula seleccionada en coordenadas esféricas. Suponemos que, referido al sistema de coordenadas cartesianas que hemos erigido, el vector de velocidad de la molécula seleccionada es\(\left(v^*,{\theta }^*,{\varphi }^*\right)\). El vector\(\mathop{v^*}\limits^{\rightharpoonup}t\), dibujado desde el origen de nuestro sistema cartesiano hasta el punto de impacto en la pared, sigue la trayectoria de la molécula de tiempo cero a tiempo\(t\). El\(z\) componente -del vector de velocidad molecular es normal al plano de\(A\) en el punto de impacto; la magnitud del\(\ z\) -componente\(v^*{\mathrm{cos} {\theta }^*\ }\). La distancia perpendicular desde el plano de A al\(xy\) plano -plano del sistema cartesiano es\(v^*t{\mathrm{cos} {\theta }^*\ }\).

Suponemos que la colisión es perfectamente elástica. Antes de la colisión, el componente de velocidad perpendicular a la pared es\(v_z=v^*{\mathrm{cos} {\theta }^*\ }\). Después, lo es\(v_z={-v}^*{\mathrm{cos} {\theta }^*\ }\). Sólo este cambio en el\(v_z\) componente contribuye a la fuerza en la pared interior\(A\). (Los\(v_y\) componentes\(v_x\) y no se modifican por la colisión.) Durante la colisión, el cambio de impulso de la molécula es\({-2mv}^*{\mathrm{cos} {\theta }^*\ }\). Durante nuestro periodo de observación, la fuerza promedio sobre la molécula es así\({\left({-2mv}^*{\mathrm{cos} {\theta }^*\ }\right)}/{t}\). La fuerza que la molécula ejerce sobre la pared es\({\left({2mv}^*{\mathrm{cos} {\theta }^*\ }\right)}/{t}\), y de ahí la contribución que esta colisión particular, por una molécula viajando a velocidad\(v^*\), hace a la presión sobre la pared es

\[P_1\left(v^*\right)=\frac{2mv^* \mathrm{cos} {\theta }^*\ }{At}\]

Queremos encontrar la presión sobre el segmento\(A\) de la pared que resulta de todos los impactos posibles. Para ello, reconocemos que cualquier otra molécula cuyos componentes de velocidad sean\(v^*\)\({\theta }^*\), y\({\varphi }^*\), y cuya ubicación en el tiempo\(t=0\) le permita alcanzar\(A\) dentro del tiempo\(t\), hace la misma contribución a la presión que la molécula seleccionada. Comencemos asumiendo que las velocidades de todos los N de las moléculas en el volumen,\(V\), son las mismas que las de la molécula seleccionada. En este caso, podemos encontrar el número de moléculas en el contenedor que pueden alcanzar\(A\) en el tiempo\(t\) considerando un segmento tubular del interior del contenedor. El eje largo de este tubo es paralelo al vector de velocidad de la molécula seleccionada. Los lados de este tubo cortan la pared del contenedor a lo largo del perímetro de\(A\). Este tubo también corta el\(xy\) -plano (el\(z=0\) plano) de nuestro sistema de coordenadas de tal manera que se haga una réplica exacta de\(A\) en este plano. Llama a esta réplica\(A^o\).

El área de\(A^o\) es\(A\); el plano de\(A^o\) es paralelo al plano de\(A\); y la distancia perpendicular entre el plano de\(A\) y el plano de\(A^o\) es\(v^*t{\mathrm{cos} {\theta }^*\ }\). El volumen de este tubo es por lo tanto\({Av}^*t{\mathrm{cos} {\theta }^*\ }\). Dado que hay\({N}/{V}\) moléculas por unidad de volumen, el número total de moléculas en el tubo es\({\left(ANv^*t{\mathrm{cos} {\theta }^*\ }\right)}/{V}\). Cuando asumimos que cada molécula tiene componentes de velocidad\(v^*\)\({\theta }^*\),, y\({\varphi }^*\), todas las moléculas en el tubo alcanzan\(A\) dentro del tiempo\(t\), porque cada una de ellas viaja paralela a la molécula seleccionada, y cada una de ellas está inicialmente al menos tan cerca\(A\) como es la molécula seleccionada. Por lo tanto, cada molécula en el tubo contribuye\(P_1\left(v^*\right)={2mv^*{\mathrm{cos} {\theta }^*\ }}/{At}\) a la presión a\(A\). La presión total es la presión por molécula multiplicada por el número de moléculas:

\[\left(\frac{2mv^* \mathrm{cos} {\theta }^*\ }{At}\right)\left(\frac{ANv^*t \mathrm{cos} {\theta }^*\ }{V}\right)=\frac{2mN \left(v^* \mathrm{cos} {\theta }^*\right)^2}{V}\]

Sin embargo, las velocidades moleculares no son todas iguales, y la contribución de presión\({2mN{\left(v^*{\mathrm{cos} {\theta }^*\ }\right)}^2}/{V}\) se realiza solo por esa fracción de las moléculas cuyos componentes de velocidad se encuentran en los intervalos\({\theta }^*<\theta <{\theta }^*+d\theta\) y\({\varphi }^*<\varphi <{\varphi }^*+d\varphi\). Esta fracción es

\[\rho \left(v^*,{\theta }^*,{\varphi }^*\right) \left(v^*\right)^2 \mathrm{sin} {\theta }^*dvd\theta d\varphi = \left(\frac{\lambda }{2\pi }\right)^{3/2} \left(v^*\right)^2\mathrm{exp}\left(\frac{-\lambda \left(v^*\right)^2}{2}\right)\mathrm{sin} {\theta }^*dvd\theta d\varphi\]

de manera que la contribución de presión de las moléculas cuyos componentes de velocidad se encuentran en estos rangos es

\[dP=\frac{2mN\left(v^* \mathrm{cos} {\theta }^* \right)^2}{V}\times \left(\frac{\lambda }{2\pi }\right)^{3/2} \left(v^*\right)^2\mathrm{exp}\left(\frac{-\lambda \left(v^*\right)^2}{2}\right) \mathrm{sin} {\theta }^*dvd\theta d\varphi\]

La presión total en\(A\) es solo la suma de las contribuciones de las moléculas con todas las combinaciones posibles de velocidades\(v^*\),\({\theta }^*\), y\({\varphi }^*\). Para encontrar esta suma, integramos sobre todos los vectores de velocidad posibles. Los valores permitidos de\(v\) son\(0\le v<\infty\). No hay limitaciones en los valores de\(\varphi\); tenemos\(0\le \varphi <2\pi\). Sin embargo, dado que todas las moléculas impactantes deben tener un componente de velocidad en la dirección z positiva, los posibles valores de se\(\theta\) encuentran en el intervalo\(0\le \theta <{\pi }/{2}\). Designamos la velocidad de la molécula original como\(\left(v^*,{\theta }^*,{\varphi }^*\right)\) y conservamos esta notación para que sea lo más específica posible al describir el tubo delimitado por\(A\) y\(A^o\). Sin embargo, los componentes de velocidad de una molécula arbitraria pueden tener cualquiera de los valores permitidos. Para integrar (Ver Apéndice D) sobre los valores permitidos, bajamos los superíndices. La presiónpresión:en la pared en\(A\) se convierte

\[P=\frac{2mN}{V} \left(\frac{\lambda }{2\pi }\right)^{3/2}\times\]

\[\int^{\infty }_0 v^4exp\left(\frac{-\lambda v^2}{2}\right)dv \int^{\pi /2}_0 \mathrm{cos}^2 \theta \ \mathrm{sin} \theta \ d\theta \int^{2\pi }_0 d\varphi\]

\[=\frac{2mN}{V} \left(\frac{\lambda }{2\pi }\right)^{3/2}\left[ \frac{3}{8} \left(\frac{2}{\lambda }\right)^2 \left(\frac{2\pi }{\lambda }\right)^{1/2}\right]\left[\frac{1}{3}\right]\left[2\pi \right]=mN/V\lambda \]

y el producto de presión-volumen se convierte en

\[PV=\frac{mN}{\lambda }\]

Ya que\(m,\)\(N\), y\(\lambda\) son constantes, esta es la ley de Boyle. Equiparando este producto de presión-volumen con el dado por la ecuación de gas ideal, tenemos\({mN}/{\lambda }=NkT\) para que

\[\lambda =\frac{m}{kT}\]

Finalmente, la ecuación de Maxwell-Boltzmann se convierte en

\[\frac{df_v\left(v\right)}{dv}=4\pi \left(\frac{m}{2\pi kT}\right)^{3/2}v^2\mathrm{exp}\left(\frac{-mv^2}{2kT}\right)\]

y la densidad de probabilidad se convierte en

\[\rho \left(v,\theta ,\varphi \right)= \left(\frac{m}{2\pi kT}\right)^{3/2}v^2\mathrm{exp}\left(\frac{-mv^2}{2kT}\right)\]

Esta derivación se puede refundir como un cálculo del valor esperado de la presiónpresión:valor esperado. Para ello, reformulamos nuestra descripción del sistema: Una molécula cuyos componentes de velocidad son\(\left(v^*,{\theta }^*,{\varphi }^*\right)\) crea una presión\({2mv^*{\mathrm{cos} {\theta }^*\ }}/{At}\) sobre el área\(A\) con una probabilidad de\(Av^*t\mathrm{cos} {\theta }^*/{V}\). (Este último término es la probabilidad de que una molécula, cuya velocidad es\(\left(v^*,{\theta }^*,{\varphi }^*\right)\), se encuentre, en el momento\(t=0\), en una ubicación desde la que pueda llegar\(A\) dentro del tiempo\(t.\) Si la molécula va a golpear la pared dentro del tiempo\(t\), en\(t=0\) el momento la molécula debe estar dentro del segmento tubular de volumen es\(Av^*t\mathrm{cos} {\theta }^*\). La probabilidad de que la molécula esté dentro de este segmento tubular es igual a la fracción del volumen total que ocupa este segmento). Por lo tanto, el producto

\[\left(\frac{2mv^*\mathrm{cos} {\theta }^*}{At}\right)\left(\frac{Av^*t \mathrm{cos} {\theta }^*}{V}\right)=\frac{2m}{V} \left(v^* \mathrm{cos} {\theta }^* \right)^2\]

es la contribución de presión de una molécula con velocidad\(\left(v^*,{\theta }^*,{\varphi }^*\right)\), cuando\({\theta }^*\) está en el intervalo\(0\le {\theta }^*<{\pi }/{2}\). La presión total por molécula es el valor esperado de esta contribución de presión; el valor esperado es la integral, sobre todo el volumen del espacio de velocidad, de la contribución de presión por la función de densidad de probabilidad para velocidades.

Es útil ver la ecuación de Maxwell-Boltzmann como el producto de un término

\[\mathrm{exp}\left({-mv^2}/{2kT}\right)\]

—llamado factor Boltzmann factor Boltzmann— y un término preexponencial que es proporcional al número de formas en que una molécula puede tener una velocidad dada,\(v\). Si no hubiera restricciones en la velocidad de una molécula, esperaríamos que el número de moléculas con velocidades entre\(v\) y\(v+dv\) aumentaría a medida que\(v\) aumenta, porque la probabilidad de que una molécula tenga una velocidad entre\(v\) y\(v+dv\) sea proporcional al volumen en espacio de velocidad de una concha esférica de espesor\(dv\). El volumen de una concha esférica de espesor\(dv\) es\(4\pi v^2dv\), que aumenta a medida que el cuadrado de\(v\). Sin embargo, el número de moléculas con grandes valores de\(v\) está limitado por la conservación de energía. Dado que la energía total de una colección de moléculas es limitada, solo una pequeña proporción de las moléculas puede tener velocidades muy grandes. El factor Boltzmann introduce esta restricción. Una molécula cuya masa es m y cuya velocidad escalar es\(v\) tiene energía cinética\(\epsilon ={mv^2}/{2}\). El factor Boltzmann suele escribirse como\(\mathrm{exp}\left({-\epsilon }/{kT}\right)\).