4.7: Prueba Experimental de la Densidad de Probabilidad Maxwell-Boltzmann

Existen numerosas aplicaciones de la ecuación de Maxwell-Boltzmann. Estos incluyen predicciones de frecuencias de colisión, trayectorias libres de medias, velocidades de efusión y difusión, la conductividad térmica de los gases y viscosidades de los gases. Estas aplicaciones son importantes, pero ninguna de ellas es una prueba directa de la validez de la ecuación de Maxwell-Boltzmann.

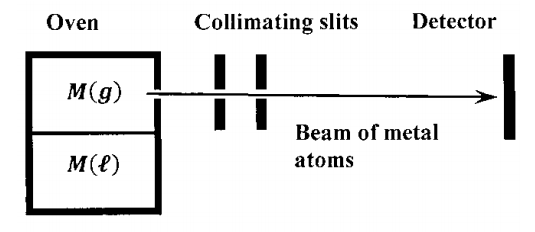
La validez de la ecuación se ha demostrado directamente en experimentos en los que se produce un gas de átomos metálicos en un horno a una temperatura muy alta. Como se esboza en la Figura 4, se permite que el gas escape a una cámara de vacío a través de un orificio muy pequeño en el costado del horno. Los átomos que escapan inciden en una o más placas metálicas. Ranuras estrechas cortadas en estas placas detienen cualquier átomo de metal cuyas trayectorias de vuelo no pasan a través de las rendijas. Esto produce un haz:de átomos metálicos de átomos metálicos cuya distribución de velocidad es la misma que la del gas metal-átomo dentro del horno. Se mide la velocidad a la que los átomos metálicos llegan a un detector. Se utilizan diversos métodos para traducir la tasa de llegada de átomos en una medición de su velocidad.

Figura 4. Produciendo un haz de átomos metálicos.

Un dispositivo utiliza un tambor cilíndrico sólido, el cual gira sobre su eje cilíndrico. Como se esboza en la Figura 5, se corta una ranura en espiral en la cara cilíndrica de este tambor. Esta ranura se corta con un paso constante. Cuando el tambor gira a una velocidad constante, un átomo que viaja a una constante

la velocidad paralela al eje cilíndrico puede atravesar la longitud del tambor mientras permanece dentro de la ranura. Es decir, para una velocidad de rotación dada, hay una velocidad crítica a la que un átomo puede viajar en línea recta mientras permanece en el medio de la ranura todo el camino de un extremo del tambor al otro. Si el átomo se mueve significativamente más rápido o más lento que esta velocidad crítica, choca con, y se pega a, un lado u otro de la ranura.

Figura 5. Dispositivo para seleccionar átomos metálicos que tengan una velocidad especificada.

Dado que la ranura tiene un ancho finito, los átomos cuyas velocidades se encuentran en un rango estrecho alrededor de la velocidad crítica pueden atravesar la ranura sin chocar con uno de los lados.

Supongamos que la ranura está cortada de manera que la espiral recorra la mitad del cilindro. Es decir, si proyectamos la espiral sobre una de las caras circulares del tambor, la proyección atraviesa un ángulo de\({180}^o\) sobre la cara. Para permanecer en el medio de esta ranura todo el camino de un extremo del tambor al otro, el átomo debe recorrer la longitud del tambor cilíndrico exactamente en el mismo tiempo que tarda el tambor en hacer una media rotación. Deja que la velocidad crítica sea\(v_{critical}\). Entonces el tiempo requerido para que el átomo atraviese la longitud, d, del tambor es\({d}/{v_{critial}}\). Si el tambor gira a u ciclos/seg, el tiempo requerido para que el tambor haga media rotación es\({1}/{2u}\). Así, el átomo permanecerá en el medio de la ranura todo el camino a través del tambor si

\[v_{critial}=2ud\]

Al variar la velocidad de rotación, podemos variar la velocidad crítica.

Debido a que la ranura tiene un ancho finito, los átomos cuyas velocidades están en un rango\(v_{min}<v_{max}\) pueden atravesar con éxito la ranura. El hecho de que un átomo en particular pueda hacerlo depende de su velocidad, de dónde entra en la ranura, y del ancho de la ranura. Deje que el ancho de la ranura sea\(w\) y el radio del tambor sea\(r\), donde se construye el tambor con\(r\gg w\). Un átomo más lento que ingresa a la ranura lo antes posible, cuando el borde de entrada de la ranura se encuentra por primera vez con el haz de átomos, puede atravesar la longitud de la ranura en un tiempo más largo,\(t_{max}\). Un punto en la circunferencia del tambor viaja con velocidad\(2\pi ru\). El átomo más lento atraviesa la longitud del tambor mientras que un punto en la circunferencia del tambor recorre una distancia\(\pi r+w\). (Para interceptar el átomo más lento, el borde posterior de la ranura debe recorrer una distancia igual a la mitad de la circunferencia del tambor,\(\pi r\), más el ancho de la ranura,\(w\).) El tiempo requerido para esta rotación es el tiempo máximo que una partícula puede tardar en atravesar la longitud, por lo que

\[t_{max}=\left(\pi r+w\right)/\left(2\pi ru\right)\]y\[v_{min}=d/t_{max}=2\pi rud/\left(\pi r+w\right)\]

Un átomo rápido que entra en la ranura en el último momento posible, cuando el borde de salida de la arboleda simplemente abandona el haz de átomos, todavía puede atravesar la ranura si lo hace en el tiempo,\(t_{min}\) que toma el borde de salida de la ranura para recorrer una distancia\(\pi r-w\). Entonces,

\[t_{min}=\left(\pi r-w\right)/\left(2\pi ru\right)\]y\[v_{max}=d/t_{min}=2\pi rud/\left(\pi r-w\right)\]

A una velocidad de rotación dada, el tambor pasará átomos cuyas velocidades están en el rango

\[\Delta v=v_{max}-v_{min}=2ud\left(\frac{\pi r}{\pi r-w}-\frac{\pi r}{\pi r+w}\right)=2ud\left(\frac{2\pi rw}{\left(\pi r\right)^2-w^2}\right)\approx v_{critical}\left(\frac{2w}{\pi r}\right)\]

Así que\[\frac{\Delta v}{v_{critial}}\approx \frac{2w}{\pi r}\]

La fracción de los átomos incidentes que atraviesan exitosamente la ranura es igual a la fracción que tiene velocidades en el intervalo\(\Delta v\) centrado en la velocidad crítica,\(v_{critical}=2ud\).