4.15: La geometría de una colisión entre moléculas esféricas

Hasta ahora no nos hemos preocupado por la orientación relativa de un par de moléculas colisionantes. Queremos desarrollar un modelo más detallado para el proceso de colisión\({}^{1}\) en sí, y el primer paso es especificar a qué nos referimos con orientación relativa.

Como antes, consideramos una molécula de tipo que\(1\) se mueve con la velocidad relativa\(v_{12}\) a través de un gas de\(\ 2\) moléculas de tipo estacionario. En unidad de tiempo, la molécula\(1\) recorre una distancia\(v_{12}\) y choca con muchas moléculas de tipo\(2\). Podemos caracterizar cada colisión por el ángulo,\(\theta\), entre el vector de velocidad y la línea de centros del par colisionante. Por colisiones de mirada, tenemos\(\theta ={\pi }/{2}\). Para colisiones frontales, tenemos\(\theta =0\). Siendo todos los demás iguales, la colisión será más violenta cuanto menor sea el ángulo\(\theta\). Evidentemente, podemos describir el efecto promedio de las colisiones de manera más completa si podemos especificar la frecuencia de colisiones en función de\(\theta\). Más precisamente, queremos encontrar la frecuencia de colisiones en las que se encuentra este ángulo entre\(\theta\) y\(\theta +d\theta\).

Cuando ocurre una colisión, la distancia entre los centros moleculares es\({\sigma }_{12}\). Podemos decir que el centro de la molécula\(2\) está en un punto particular en la superficie de una esfera, de radio\({\sigma }_{12}\), circunscrito alrededor de la molécula\(1\). Como se esboza en la Figura 13, podemos rotar la línea de centros alrededor del vector de velocidad, manteniendo constante el ángulo entre ellos\(\theta\). Al hacerlo, la línea de centros traza un círculo en la superficie de la esfera; las colisiones que ponen el centro de la molécula\(\ 2\) en dos puntos cualesquiera de este círculo son completamente equivalentes. Dejando que el radio de este círculo sea\(r\), lo vemos\(r=\sigma_{12}\mathrm{sin} \theta\). Evidentemente, para las moléculas esféricas, especificar\(\theta\) especifica la orientación relativa en el momento de la colisión.

Si ahora permitimos\(\theta\) variar por\(d\theta\), el locus de puntos equivalentes en la esfera circunscrita se expande a una banda. Medido a lo largo de la superficie de la esfera, el ancho de esta banda es\({\sigma }_{12}d\theta\). A medida que la molécula\(1\) se mueve a través del gas de\(2\) moléculas de tipo estacionario, esta banda barre una cubierta cilíndrica. Molécula\(1\) colisiona, en un ángulo entre\(\theta\) y\(\theta +d\theta\), con cada tipo de\(2\) molécula en este caparazón cilíndrico. Por el contrario, cada tipo de\(2\) molécula en esta cubierta cilíndrica choca con\(1\) la molécula en un ángulo entre\(\theta\) y\(\theta +d\theta\). (Molécula\(1\) también colisiona con muchos otros tipos de\(2\) moléculas, pero esas colisiones están en otros ángulos; tienen diferentes orientaciones). En unidad de tiempo, la longitud de la carcasa cilíndrica es\(v_{12}\). El volumen de la carcasa cilíndrica es su longitud por su área de sección transversal.

Figura 13. La geometría de las colisiones entre esferas.

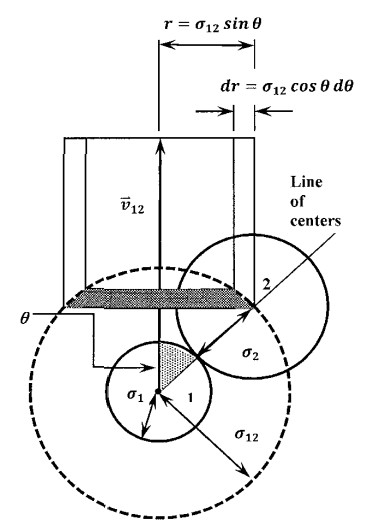
La sección transversal de la cubierta cilíndrica es un anillo circular. Al ver el anillo como una tira rectangular cuya longitud es la circunferencia de la concha y cuyo ancho es el grosor radial del anillo, el área del anillo es la circunferencia por el grosor radial. Dado que el radio de la concha es\(r={\sigma }_{12}\mathrm{sin} \theta\), su circunferencia es\(2\pi {\sigma }_{12} \mathrm{sin} \theta\). El grosor radial del anillo es solo el cambio en la distancia,\(r={\sigma }_{12}\mathrm{sin} \theta\), entre el vector de velocidad y la pared del cilindro cuando\(\theta\) cambia en una pequeña cantidad\(d\theta\). Esto es

\[dr=\left(\frac{dr}{d\theta }\right)d\theta ={\sigma }_{12} \mathrm{cos} \theta d\theta\]

Por lo tanto, el área del anillo es

\[2\pi {\sigma }^2_{12} \mathrm{sin} \theta \mathrm{cos} \theta d\theta\]

y el volumen de la cubierta cilíndrica barrida por una molécula tipo 1 (viajando exactamente a la velocidad\(v_{12}\)) en unidad de tiempo es

\[2\pi {\sigma }^2_{12}v_{12} \mathrm{sin} \theta \mathrm{cos} \theta d\theta\]

Nuevamente dejamos\(N_2\) ser el número de moléculas de tipo\(2\) por unidad de volumen. El número de colisiones, por unidad de tiempo, entre una molécula de tipo\(1\), viajando exactamente\(v_{12}\), y moléculas de tipo\(2\), en las que el ángulo de colisión se encuentra entre\(\theta\) y\(\theta +d\theta\) es

\[2\pi N_2{\sigma }^2_{12}v_{12} \mathrm{sin} \theta \mathrm{cos} \theta d\theta\]

Necesitamos encontrar el número de tales colisiones en las que la velocidad relativa se encuentra entre\(v_{12}\) y\(v_{12}+dv_{12}\). La probabilidad de encontrar\(v_{12}\) en este intervalo es\(\left(df\left(v_{12}\right)/dv_{12}\right)dv_{12}\). \(d\widetilde{\nu }_{12}\left({\nu }_{12},\theta \right)\)Sea el número de colisiones realizadas en unidad de tiempo, por una\(1\) molécula tipo, con moléculas de tipo\(2\), en las que el ángulo de colisión está entre\(\theta\) y\(\theta +d\theta\), y la velocidad relativa escalar está entre\(v_{12}\) y\(v_{12}+dv_{12}\). Esto es solo el número de colisiones cuando la velocidad relativa se\(v_{12}\) multiplica por la probabilidad de que la velocidad relativa esté entre\(v_{12}\) y\(v_{12}+dv_{12}\). Tenemos el resultado que necesitamos:

\[ \begin{aligned} d\widetilde{\nu }_{12}\left(v_{12},\theta \right) & = 2\pi N_2{\sigma }^2_{12}v_{12}\left(\frac{df\left(v_{12}\right)}{dv_{12}}\right) \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta dv_{12} \\ ~ & =8 { \pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2}v^3_{12}exp\left(\frac{-\mu v^2_{12}}{2kT}\right) \times \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta dv_{12} \end{aligned}\]

Reconociendo que los posibles valores de\(\theta\) mentira en el rango\(0\le \theta <{\pi }/{2}\) y que los posibles valores de\(v_{12}\) mentira en el rango\(0\le v_{12}<\infty\), podemos encontrar la frecuencia de todas las colisiones posibles,\(\widetilde{\nu }_{12}\), sumando sobre todos los valores posibles de\(\theta\) y\(v_{12}\). Es decir,

\[\begin{aligned} \widetilde{\nu }_{12} & =8{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2}\int^{\infty }_0 v^3_{12}exp\left(\frac{-\mu v^2_{12}}{2kT}\right) dv_{12} \times \int^{\pi /2}_0 \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta \\ ~ & =8{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2}\left[2 \left(\frac{kT}{\mu }\right)^2\right]\left[\frac{1}{2}\right] \\ ~ & =N_2{\sigma }^2_{12} \left(\frac{8\pi kT}{\mu }\right)^{1/2} \end{aligned}\]

En la Sección 4.12, obtuvimos este resultado por un argumento ligeramente diferente, en el que no consideramos explícitamente el ángulo de colisión,\(\theta\).