4.16: La energía de una colisión entre moléculas de gas

Es útil extender nuestro modelo de colisiones moleculares para suponer que una o ambas moléculas pueden sufrir cambios químicos como resultado de la colisión. Al hacerlo, estamos introduciendo algunas ideas que desarrollamos más en el Capítulo 5.

Cuando preguntamos por los factores que determinan si tal reacción puede ocurrir, puede haber varias posibilidades. Queremos enfocarnos en uno de esos factores: la violencia de la colisión. Esperamos que una colisión sea más probable que resulte en una reacción cuanto más fuerte se golpeen las dos moléculas entre sí. Cuando tratamos de formular nuestras bases para esta expectativa, vemos que la idea subyacente es que una colisión deforma las moléculas colisionantes. Cuanto más violenta sea la colisión, mayor será la deformación y mayor será la probabilidad de reacción.

Para proceder, necesitamos ser más precisos sobre lo que queremos decir con la violencia de la colisión. Evidentemente, lo que tenemos en mente tiene dos componentes: la velocidad relativa y el ángulo de colisión. Si la colisión es de un vistazo\(\theta ={\pi }/{2}\), esperamos que el efecto sobre las moléculas sea mínimo, aunque la velocidad relativa sea alta. Por otro lado, una colisión directa,\(\theta \approx 0\), podría llevar a la reacción aunque la velocidad relativa sea comparativamente baja. Con estas ideas en mente, vemos que un modelo razonable es suponer que las fuerzas que actúan a lo largo de la línea de centros pueden conducir a la reacción, mientras que las fuerzas que actúan perpendiculares a la línea de centros no pueden. Si las moléculas colisionantes tienen formas complejas, esta puede ser una suposición pobre.

También necesitamos una forma de especificar cuánta deformación ocurre en una colisión. Si queremos especificar la deformación describiendo cambios específicos en las estructuras moleculares, este es un problema complejo. Para un modelo general, sin embargo, podemos evitar este nivel de detalle. Para ello, reconocemos que cualquier deformación sólo puede proceder hasta que el trabajo realizado en la deformación de las moléculas sea igual a la energía que se puede gastar para realizar este trabajo. A medida que las moléculas se deforman, sus energías potenciales cambian. El cambio máximo en esta energía potencial es solo la cantidad de energía cinética que las moléculas colisionantes pueden usar para efectuar esta deformación. Podemos identificar esta cantidad de energía cinética con el componente de la energía cinética de las moléculas que se asocia con su movimiento relativo a lo largo de la línea de centros.

Si ahora asociamos un nivel umbral de deformación con la ocurrencia de un cambio químico, la energía cinética requerida para efectuar esta deformación determina si el cambio puede ocurrir. Si la energía cinética disponible es menor que la requerida para alcanzar el nivel umbral de deformación, la reacción no puede ocurrir. Si la energía cinética disponible excede este mínimo, se produce la reacción. Llamamos a la energía cinética mínima la energía de activación y generalmente la representamos por el símbolo\({\epsilon }_a\). (Al discutir las velocidades de reacción, generalmente expresamos la energía de activación por mol y la representamos como\(E_a\), donde\[E_a=\overline{N}{\epsilon }_a.)\]

Podemos aplicar estas ideas a nuestro modelo de colisión entre moléculas esféricas. En la Sección 4.10, desarrollamos coordenadas de velocidad relativa. De ello se deduce que podemos divisar la energía cinética del sistema de dos partículas en un componente que depende de la velocidad del centro de masa y un componente que depende de la velocidad relativa. Es decir, tenemos

\[ \begin{aligned} KE & =\frac{m_1v^2_1}{2}+\frac{m_2v^2_2}{2} \\ & =\frac{m_1m_2}{2\mu }\left(\dot{x}^2_0+\dot{y}^2_0+z^2_0\right)+\mu \left(\dot{x}^2_{12}+\dot{y}^2_{12}+\dot{z}^2_{12}\right) \\ & =\frac{m_1m_2v^2_0}{2\mu }+\frac{\mu v^2_{12}}{2} \end{aligned}\]

Solo el componente que depende de la velocidad relativa puede contribuir a la deformación de las moléculas colisionantes. La velocidad relativa se puede resolver en componentes paralelos y perpendiculares a la línea de centros. El componente paralelo es la proyección del vector de velocidad sobre la línea de centros. Esto es\(v_{12} \mathrm{cos} \theta\), y el componente perpendicular es\(v_{12}\mathrm{sin} \theta\). Vemos que la energía cinética asociada al movimiento relativo de las partículas 1 y 2 tiene un componente

\[\frac{\mu v^2_{12} \mathrm{cos}^2 \theta}{2}\]

paralelo a la línea de centros y un componente

\[\frac{\mu v^2_{12} \mathrm{sin}^2 \theta}{2}\]

perpendicular a ella.

La idea de que la energía cinética paralela a la línea de centros debe exceder\({\varepsilon }_a\) para que ocurra la reacción ahora se puede expresar como el requisito de que

\[{\epsilon }_a<\frac{\mu v^2_{12} \mathrm{cos}^2 \theta}{2}\]

Cuando consideramos todas las posibles colisiones entre las moléculas 1 y 2, el ángulo de colisión varía de 0 a\({\pi }/{2}\). Sin embargo, solo aquellas colisiones para las que\(v_{12}\) satisfaga la desigualdad anterior tendrán suficiente energía cinética a lo largo de la línea de centros para que ocurra la reacción. El valor más pequeño de\(v_{12}\) lo que puede satisfacer esta desigualdad se produce cuando\(\theta =0\). Esta velocidad relativa mínima es

\[v^{minimun}_{12}= \left(2{\epsilon }_a/{\mu }\right)^{1/2}\]

Para velocidades relativas superiores a este mínimo, las colisiones son efectivas solo cuando

\[\mathrm{cos} \theta > \left(2{\epsilon }_a/ \mu v^2_{12}\right)^{1/2}\]

para que

\[\theta < \mathrm{cos}^{-1} \left(2{\epsilon }_a/\mu v^2_{12}\right)^{1/2}\]

Designemos la frecuencia de colisiones satisfaciendo estas restricciones como\(\widetilde{\nu }_{12}\left({\epsilon }_a\right)\). Recordando que

\[d\widetilde{\nu }_{12}\left({\nu }_{12},\theta \right)= 8{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2}v^3_{12} \mathrm{exp}\left(\frac{-\mu v^2_{12}}{2kT}\right) \times \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta dv_{12}\]

vemos que

\[\widetilde{\nu }_{12}\left({\varepsilon }_a\right)=8{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2} \times \int^{\infty }_{v_{12}=\left(2{\epsilon }_a/{\mu }\right)^{1/2}} \int^{\mathrm{cos}^{-1} \left(2{\epsilon }_a/ \mu v^2_{12}\right)^{1/2}}_{\theta =0} v^3_{12}\mathrm{\ exp}\left(\frac{-\mu v^2_{12}}{2kT}\right) \times \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta dv_{12}\]

La integral que implica\(\theta\) es

\[\int^{\mathrm{cos}^{-1} \left( 2{\epsilon }_a/\mu v^2_{12}\right)^{1/2}}_{\theta =0} \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta = \left[\frac{\mathrm{sin}^2 \theta}{2}\right]^{\mathrm{cos}^{-1} \left(2{\epsilon }_a/\mu v^2_{12}\right)^{1/2}}_0=\frac{1}{2}\left[1-\frac{2{\epsilon }_a}{\mu v^2_{12}}\right]\]

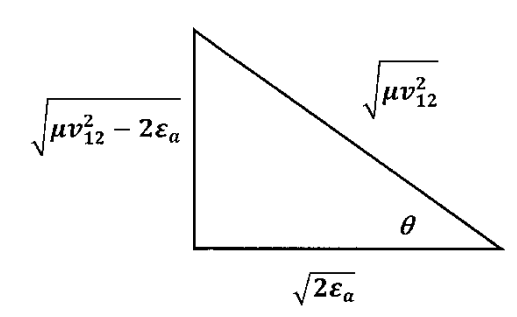
donde, para evaluar la integral en su límite superior, observamos que el ángulo\(\theta ={{\mathrm{cos}}^{-1} {\left({2{\epsilon }_a}/{\mu v^2_{12}}\right)}^{{1}/{2}}\ }\) se encuentra en un triángulo cuyos lados tienen longitudes como se indica en la Figura 14.

Figura 14. Ángulo máximo para una colisión efectiva.

La frecuencia de colisión se convierte en

\[\widetilde{\nu }_{12}\left({\epsilon }_a\right)=4{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3}/{2}\times \int^{\infty }_{v_{12}=\left(2{\epsilon }_a/{\mu }\right)^{1/2}} \left[1-\frac{2{\epsilon }_a}{\mu v^2_{12}}\right]v^3_{12}\ \mathrm{exp}\left(\frac{-\mu v^2_{12}}{2kT}\right)dv_{12}\]

Esta integral se puede evaluar haciendo la sustitución\(v_{12}= \left({2\epsilon }/{\mu }\right)^{1/2}\). El límite inferior de integración se convierte\({\epsilon }_a\); tenemos

\[ \begin{aligned} \int^{\infty }_{v_{12}=\left(2{\epsilon }_a/{\mu }\right)^{1/2}} & \left[1-\frac{2{\epsilon }_a}{\mu v^2_{12}}\right]v^3_{12}\ \mathrm{exp}\left(\frac{-\mu v^2_{12}}{2kT}\right)dv_{12} \\ & =\frac{2}{{\mu }^2}\int^{\infty }_{{\epsilon }_a} \left(\epsilon -{\epsilon }_a\right)\mathrm{exp}\left(\frac{-\epsilon }{kT}\right)d\epsilon \\ & =2 \left(\frac{kT}{\mu }\right)^2\mathrm{exp}\left(\frac{-{\epsilon }_a}{kT}\right) \end{aligned}\]

Entonces

\[\begin{aligned} \widetilde{\nu }_{12}\left({\varepsilon }_a\right) & =4{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2}\times 2 \left(\frac{kT}{\mu }\right)^2\mathrm{exp}\left(\frac{-{\epsilon }_a}{kT}\right) \\ & =N_2{\sigma }^2_{12} \left(\frac{8\pi kT}{\mu }\right)^{1/2}\mathrm{exp}\left(\frac{-{\epsilon }_a}{kT}\right) \end{aligned}\]

Tenga en cuenta que cuando\({\epsilon }_a=0\), esto se reduce a la misma expresión para la\(\widetilde{\nu }_{12}\) que hemos obtenido dos veces anteriormente. La frecuencia de colisiones que tienen energía cinética a lo largo de la línea de centros en exceso de\({\epsilon }_a\) depende exponencialmente de\(-{\epsilon }_a/{kT}\). Siendo todos los demás iguales, esta frecuencia aumenta a medida que aumenta la temperatura; disminuye a medida que aumenta la energía de activación.