9.2: El ciclo del carnot para un gas ideal y el concepto de entropía
- Page ID
- 74253
Históricamente, la máquina de vapor fue la primera máquina para convertir el calor en trabajos que podían ser explotados a gran escala. La máquina de vapor jugó un papel importante en la revolución industrial y, por lo tanto, en el desarrollo de la economía actual intensiva en tecnología. Fue importante también en el desarrollo de los conceptos básicos de la termodinámica. Una máquina de vapor produce trabajo cuando se introduce vapor caliente bajo presión en un cilindro, impulsando un pistón hacia afuera. Un eje conecta el pistón a un volante. Cuando el eje de conexión alcanza su mayor extensión, el vapor gastado se ventila a la atmósfera. A partir de entonces, el volante impulsa el pistón hacia adentro.
La viabilidad económica de la máquina de vapor deriva, en parte, del hecho de que el vapor gastado puede ser ventilado a la atmósfera al final de cada ciclo. Sin embargo, esta no es una característica necesaria de los motores térmicos. Podemos idear motores que alternativamente calienten y enfríen un fluido de trabajo cautivo para convertir la energía térmica en trabajo mecánico. Los motores Stirling son dispositivos prácticos de este tipo. Un motor Carnot es un motor conceptual que explota la respuesta de un sistema cerrado a los cambios de temperatura. Un motor Carnot extrae calor de un depósito a una temperatura alta fija y descarga una menor cantidad de calor en un segundo depósito a una temperatura fija más baja. Una cantidad de energía igual a la diferencia entre estos incrementos de energía térmica aparece en los alrededores como trabajo.
Para un ciclo del motor Carnot, deje que el calor transferido al sistema desde los depósitos de frío y calor sea\(q_h\) y\(q_{\ell }\) respectivamente. Tenemos\(q_h>0\) y\(q_{\ell }<0\). Que el trabajo de red realizado en el sistema sea\(w_{net}\) y el trabajo de red que aparece en los alrededores sea\({\hat{w}}_{net}\). Tenemos
\({\hat{w}}_{net}>0\),\({\hat{w}}_{net}=-w_{net}\), y\(w_{net}<0\). Para un ciclo del motor,\(\Delta E=0\), y desde
\[\Delta E=q_h+q_{\ell }+w_{net}=q_h+q_{\ell }-{\hat{w}}_{net},\]
de ello se deduce\({\hat{w}}_{net}=q_h+q_{\ell }\). El aporte de energía al motor Carnot es\(q_h\), y el trabajo útil que aparece en los alrededores es\({\hat{w}}_{net}\). (El calor aceptado por el reservorio de baja temperatura\({\hat{q}}_{\ell }=-q_{\ell }>0\),, es un producto de desecho, en el sentido de que representa energía que no se puede convertir en trabajo mecánico usando este ciclo. Todos los motores térmicos factibles comparten esta característica del motor Carnot. Por el contrario, una máquina de movimiento perpetuo del segundo tipo convierte toda su entrada de calor en trabajo; ninguna porción de su ingesta de calor queda sin usar). La eficiencia,\(\epsilon\), con la que el motor Carnot convierte la energía de entrada,\(q_h\), en energía útil de salida\({\hat{w}}_{net}\), es por lo tanto,
\[\epsilon =\frac{\hat{w}_{net}}{q_h}=\frac{q_h+q_{\ell}}{q_h}=1+\frac{q_{\ell }}{q_h}\]
Podemos generalizar nuestra consideración de los motores térmicos para incluir cualquier serie de cambios en los que un sistema cerrado intercambie calor con su entorno a más de una temperatura, entregue una cantidad positiva de trabajo al entorno y regrese a su estado original. Utilizamos el ciclo Carnot y la declaración basada en máquinas de la segunda ley para analizar sistemas que entregan trabajo de presión y volumen a los alrededores. Consideramos sistemas tanto reversibles como irreversibles. Comenzamos considerando ciclos reversibles de Carnot. Si algún sistema atraviesa reversiblemente cualquier trayectoria cerrada en un diagrama de presión-volumen, el área encerrada por la trayectoria representa el trabajo de presión-volumen intercambiado entre el sistema y sus alrededores. Si el área no es cero, la temperatura del sistema cambia durante el ciclo. Si el ciclo es reversible, todas las transferencias de calor que se produzcan deben ocurrir de manera reversible. Podemos aplicar nuestro razonamiento sobre ciclos reversibles a cualquier sistema cerrado que contenga cualquier colección de sustancias químicas, siempre y cuando cualquier cambio de fase o reacción química que se produzca lo haga de manera reversible. Esto significa que todos los cambios de fase y químicos que ocurren en el sistema deben ajustarse rápidamente a las nuevas posiciones de equilibrio que se les imponen a medida que un sistema atraviesa un ciclo de Carnot de manera reversible.
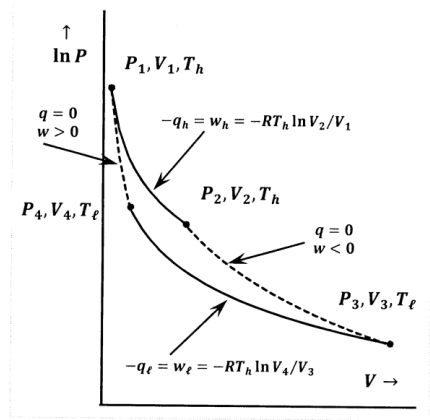
En la Figura 2, describimos el funcionamiento de un motor Carnot reversible en el que el fluido de trabajo es un gas ideal. Designamos la presión inicial, el volumen y la temperatura del sistema por\(P_1\)\(V_1\), y\(T_h\). A partir de este estado inicial, hacemos que el gas ideal sufra una expansión isotérmica reversible en la que absorbe una cantidad de calor,\(q_h\), de un depósito de calor de alta temperatura en\({\hat{T}}_h\). Designamos la presión, volumen y temperatura al final de esta expansión isotérmica como\(P_2\),\(V_2\), y\(T_h\). En un segundo paso, expandimos reversible y adiabáticamente el gas ideal hasta que su temperatura descienda a la del segundo reservorio de calor a baja temperatura. Designamos la presión, volumen y temperatura al final de esta expansión adiabática como\(P_3\),\(V_3\), y\(T_{\ell }\). Comenzamos la porción de retorno del ciclo comprimiendo reversible e isotérmicamente el gas ideal a la temperatura del reservorio frío. Continuamos con esta compresión isotérmica reversible hasta que el gas ideal alcance la presión y el volumen a partir del cual una compresión adiabática simplemente lo devolverá al estado inicial. Designamos la presión, volumen y temperatura al final de esta compresión isotérmica por\(P_4\),\(V_4\), y\(T_{\ell }\). Durante este paso, el gas ideal cede una cantidad de calor,\(q_{\ell }<0\), al reservorio de baja temperatura. Finalmente, comprimimos reversible y adiabáticamente el gas ideal a su presión, volumen y temperatura originales.
Para el paso isotérmico de alta temperatura, tenemos\[-q_h=w_h=-RT_h \ln \left(\frac{V_2}{V_1}\right)\]
y para el paso isotérmico de baja temperatura, tenemos
\[-q_{\ell }=w_{\ell }=-RT_{\ell } \ln \left(\frac{V_4}{V_3}\right)\]
Para la expansión adiabática y compresión, tenemos\[q_{exp}=q_{comp}=0\]
Los términos de energía y trabajo correspondientes son
\[{\Delta }_{exp}E=w_{exp}=\int^{T_{\ell }}_{T_h}{C_VdT}\]
para la expansión adiabática y
\[{\Delta }_{comp}E=w_{comp}=\int^{T_h}_{T_{\ell }}{C_VdT}\]
para la compresión adiabática. Las integrales de capacidad calorífica son las mismas excepto por la dirección de integración; suman cero, y nosotros tenemos\(w_{exp}+w_{comp}=0\). El trabajo neto realizado en el sistema es la suma del trabajo para estos cuatro pasos,\(w_{net}=w_h+w_{exp}+w_{\ell }+w_{comp}=w_h+w_{\ell }\). El aporte de calor se produce en el reservorio de alta temperatura, de manera que\(q_h>0\). La descarga de calor se produce en el reservorio de baja temperatura, de manera que\(q_{\ell }<0\).
Para un ciclo del motor reversible, de gas ideal Carnot,
\[\epsilon =1+\frac{q_{\ell}}{q_h}=1+\frac{RT_{\ell } \ln \left({V_4}/{V_3}\right)}{RT_h \ln \left(\frac{V_2}{V_1}\right)}\]
Debido a que los dos pasos adiabáticos implican las mismas temperaturas limitantes, la energía de un gas ideal depende únicamente de la temperatura, y\(dE=dw\) para ambos pasos, vemos en la Sección 9.7-9.20 que
\[\int^{T_{\ell }}_{T_h}{\frac{C_V}{T}}dT=-\int^{V_3}_{V_2}{\frac{R}{V}}dV=-R{ \ln \left(\frac{V_3}{V_2}\right)\ }\]
y
\[\int^{T_h}_{T_{\ell }}{\frac{C_V}{T}}dT=-\int^{V_1}_{V_4}{\frac{R}{V}}dV=-R{ \ln \left(\frac{V_1}{V_4}\right)\ }\]
Las integrales sobre\(T\) son las mismas excepto por la dirección de integración. Suman a cero, de modo que\(-R{ \ln \left({V_3}/{V_2}\right)\ }-R{ \ln \left({V_1}/{V_4}\right)\ }=0\) y
\[\frac{V_2}{V_1}=\frac{V_3}{V_4}\]
Usando este resultado, la segunda ecuación para la eficiencia reversible del motor Carnot se convierte en
\[\epsilon =1-\frac{T_{\ell }}{T_h}\]
Equiparando nuestras expresiones para la eficiencia del motor reversible Carnot, encontramos
\[\epsilon =1+\frac{q_{\ell }}{q_h}=1-\frac{T_{\ell }}{T_h}\]de la que tenemos
\[\frac{q_h}{T_h}+\frac{q_{\ell }}{T_{\ell }}=0\]
Ya que no hay transferencia de calor en los pasos adiabáticos,\(q_{exp}=q_{comp}=0,\) y podemos escribir esta suma como
\[\sum_{cycle}{\frac{q_i}{T_i}}=0\]
Si dividimos el camino alrededor del ciclo en un gran número de segmentos muy cortos, el límite de esta suma como el\(q_i\) llegar a ser muy pequeño es
\[\oint{\frac{dq^{rev}}{T}}=0\]
donde el superíndice “\(rev\)” sirve como recordatorio de que el ciclo debe ser atravesado reversiblemente. Ahora, podemos definir una nueva función,\(S\), por la expresión diferencial
\[dS=\frac{dq^{rev}}{T}\]
En esta expresión,\(dS\) se encuentra el cambio incremental en\(S\) que se produce cuando el sistema absorbe reversiblemente un pequeño incremento de calor,\({dq}^{rev}\), a una temperatura particular,\(T\). Para un gas ideal que atraviesa un ciclo Carnot, hemos demostrado que
\[\Delta S=\oint{dS}=\oint{\frac{dq^{rev}}{T}}=0\]
\(S\)es, por supuesto, la función de entropía descrita en nuestro enunciado basado en entropía de la segunda ley.
Ahora queremos ver qué nos permite deducir la afirmación basada en máquinas de la segunda ley sobre las propiedades de\(S\). Dado que el cambio en\(S\) es cero cuando un gas ideal gira alrededor de un ciclo completo de Carnot, podemos conjeturar que\(S\) es una función de estado. Por supuesto, el hecho de que\(\Delta S=0\) alrededor de un ciclo en particular no prueba que\(S\) sea una función de estado. Si\(S\) es una función de estado, debe ser cierto que\(\Delta S=0\) alrededor de cualquier ciclo sea cual sea. Ahora lo demostramos para cualquier ciclo reversible.
El comprobante tiene dos pasos. En la primera, mostramos que\(\oint{dq^{rev}/T}=0\) para una máquina que utiliza cualquier sistema reversible operando entre dos depósitos de calor a temperatura constante para convertir calor en trabajo. En el segundo paso, mostramos eso\(\oint{dq^{rev}/T}=0\) para cualquier sistema que recorra reversiblemente cualquier camino cerrado.


