9.3: El ciclo Carnot para cualquier sistema reversible

Para demostrar que\(\oint dq^{rev}/T=0\) para cualquier sistema reversible tomado alrededor de un ciclo de Carnot, primero observamos que el ciclo Carnot puede ser atravesado en sentido contrario. En este caso, el trabajo se entrega al motor y se transfiere una cantidad de calor desde el depósito de baja temperatura al depósito de alta temperatura. Operado en reversa, el motor Carnot es un refrigerador. Supongamos que tenemos dos máquinas Carnot idénticas de gas ideal, una de las cuales operamos como motor mientras operamos la otra como refrigerador. Si los configuramos para que la salida de trabajo del motor impulse el refrigerador, los efectos de operarlos juntos se cancelan por completo. El refrigerador consume exactamente la salida de trabajo del motor. Las transferencias de calor hacia y desde los depósitos de calor se compensan exactamente.

Ahora, consideremos un motor Carnot de gas ideal y cualquier otro motor reversible que extraiga calor de un depósito de alta temperatura y rechace una porción de él a un depósito de baja temperatura. Llamemos a estos motores A y B. Suponemos que uno es operado para producir trabajo en su entorno (\(w<0\)); el otro es operado para consumir esta obra y transferir energía térmica neta del reservorio de baja temperatura al depósito de alta temperatura. Deje que el trabajo neto realizado en un ciclo en las máquinas A y B sea\(w_{netA}\) y\(w_{netB}\), respectivamente. Podemos elegir hacer estos motores de cualquier tamaño que nos plazca. Vamos a dimensionarlos para que un ciclo completo de cualquiera de los motores intercambie la misma cantidad de calor con el depósito de alta temperatura. Es decir, si el depósito de alta temperatura entrega calor\(q_{hA}\) al motor A, entonces entrega calor\(q_{hB}=q_{hA}\) al motor B. La figura 3 muestra un diagrama de estos motores. Con uno funcionando como motor y el otro funcionando como refrigerador, tenemos\(q_{hA}+q_{hB}=0\). Cuando tanto el motor como el refrigerador han completado un ciclo, el reservorio de alta temperatura ha vuelto a su estado original.

Figura 3. Motor térmico y refrigerador emparejados y un sistema que los combina.

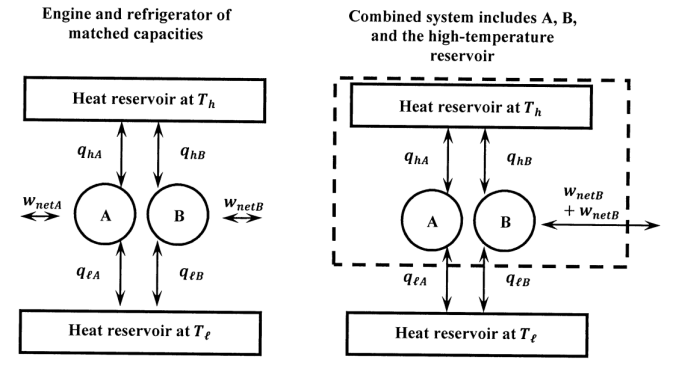
Podemos crear un dispositivo combinado que consiste en A funcionando como motor, B funcionando como refrigerador y el depósito de alta temperatura. La Figura 3 también representa un diagrama de esta combinación. Cuando ejecuta un ciclo completo, se restablece la condición inicial del dispositivo combinado. Por lo tanto, dado que E es una función de estado, tenemos

\[\begin{align} \Delta E &= w_{netA}+q_{hA}+q_{\ell A}+w_{netB}+q_{hB}+q_{\ell B} \\[4pt] &=w_{netA}+w_{netB}+q_{\ell A}+q_{\ell B} \\[4pt] &=0. \end{align}\]

donde usamos la restricción\(q_{hA}+q_{hB}=0\). Consideremos la posibilidad de que\(w_{netA}+w_{netB}<0\); es decir, el dispositivo combinado haga trabajo neto en los alrededores. Entonces,\(\Delta E=0\) implica eso\(q_{\ell A}+q_{\ell B}>0\).

En este proceso cíclico, el dispositivo combinado toma una cantidad positiva de calor de un depósito de temperatura constante y entrega una cantidad positiva de trabajo al entorno. No hay otro cambio ni en el sistema ni en el entorno. Esto viola la declaración basada en máquinas de la segunda ley. Evidentemente, no es posible que el dispositivo combinado opere de la manera que hemos planteado la hipótesis. Concluimos que cualquier máquina de este tipo debe operar siempre de tal manera que\(w_{netA}+w_{netB}\ge 0\); es decir, el trabajo neto realizado en la máquina combinada durante cualquier ciclo completo debe ser cero o alguna cantidad positiva.

Al concluir que\(w_{netA}+w_{netB}\ge 0\), especificamos que la máquina combinada tiene A funcionando como motor térmico y B funcionando como refrigerador. Ahora, supongamos que invertimos sus roles, y dejamos\(w^*_{netA}\) y\(w^*_{netB}\) representamos el trabajo neto para la combinación invertida. Aplicando el mismo argumento que anteriormente, concluimos que\(w^*_{netA}+w^*_{netB}\ge 0\). Pero, dado que el sentido de operación se invierte para ambas máquinas, también debemos tener\(w^*_{netA}=-w_{netA}\) y\(w^*_{netB}=-w_{netB}\). De ahí que tengamos\(-w_{netA}-w_{netB}\ge 0\) o\(w_{netA}+w_{netB}\le 0\). Concluimos, por lo tanto, que

\[w_{netA}+w_{netB}=0\]

para cualquiera de dos motores reversibles emparejados que operan alrededor de un ciclo Carnot.

Esta conclusión puede ser reafirmada como una condición sobre las eficiencias de las dos máquinas. Las eficiencias individuales son\({\epsilon }_A=-w_{netA}/q_{hA}\) y\({\epsilon }_B=-w_{netB}/q_{hB}\).

(La ecuación de eficiencia no se ve afectada por la dirección de operación, porque cambiar la dirección cambia el signo de cada término energético en el ciclo. Cambiar la dirección de operación equivale a multiplicar tanto el numerador como el denominador por menos uno.) Entonces, de\(w_{netA}+w_{netB}=0\), se deduce que

\[{\epsilon }_Aq_{hA}+{\epsilon }_Bq_{hB}=0\]

Ya que dimensionamos A y B para que\(q_{hA}+q_{hB}=0\), tenemos

\[\epsilon_Aq_{hA}-{\epsilon }_Bq_{hA}=0\]para que\[{\epsilon }_A={\epsilon }_B\]

para cualquier motor reversible Carnot A y B que opere entre los mismos dos depósitos de calor.

Para el motor de gas ideal, encontramos\(\epsilon =1-T_{\ell }/{T_h}\). Para cualquier motor reversible Carnot, tenemos\(\Delta E=0=w_{net}+q_h+q_{\ell }\), para que\(-w_{net}=q_h+q_{\ell }\), y

\[\epsilon =\frac{-w_{net}}{q_h}=1+\frac{q_{\ell }}{q_h}\]

Esto significa que la relación de eficiencia

\[\epsilon =1-\frac{T_{\ell }}{T_h}=1+\frac{q_{\ell }}{q_h}\]

aplica a cualquier motor reversible Carnot. De ello se deduce que la integral de\(dq^{rev}/T\) alrededor de un ciclo de Carnot es cero para cualquier sistema reversible.

La validez de estas conclusiones es independiente del tipo de trabajo que produce el motor; si el motor A es un motor de gas ideal, el motor B puede estar compuesto por cualquier sistema y puede producir cualquier tipo de trabajo. Al obtener este resultado de la declaración basada en máquinas de la segunda ley, hacemos la suposición adicional de que el trabajo de presión-volumen se puede convertir completamente en cualquier otra forma de trabajo, y viceversa. Es decir, suponemos que el trabajo producido por el motor A puede accionar reversiblemente el motor B como refrigerador, ya sea que los motores A y B produzcan el mismo o diferentes tipos de trabajo.