9.4: El cambio de entropía alrededor de cualquier ciclo para cualquier sistema reversible

Cualquier sistema que atraviese reversiblemente cualquier curva cerrada en un diagrama de presión-volumen intercambia trabajo con su entorno, y el área encerrada por la curva representa la cantidad de este trabajo. En la sección anterior, encontramos\(\oint{dq^{rev}/T}=0\) para cualquier sistema que atraviese un ciclo de Carnot de manera reversible. Ahora demostramos que esto es cierto para cualquier sistema que atraviese cualquier camino cerrado de manera reversible. Esto establece que\(\Delta S\) es cero para cualquier sistema que atraviese cualquier camino cerrado de manera reversible y demuestra que\(S\), definido por\(dS=dq^{rev}/T\), es una función de estado.

Para ello, presentamos un teorema basado en la experiencia: El diagrama presión-volumen para cualquier sistema reversible puede ser embaldosado por líneas que se cruzan que representan caminos isotérmicos y adiabáticos. Estas líneas se pueden empaquetar tan densamente como queramos, de modo que el mosaico del diagrama de presión-volumen se pueda hacer tan cerca como nos plazca. El perímetro de cualquiera de las baldosas resultantes corresponde a un camino alrededor de un ciclo de Carnot. Dada cualquier curva cerrada arbitraria en el diagrama presión-volumen, podemos seleccionar un conjunto de mosaicos que simplemente lo encierra. Ver Figura 4. El perímetro de este conjunto de baldosas se aproxima a la trayectoria de la curva arbitraria. Dado que el mosaico se puede hacer tan fino como queramos, el perímetro del conjunto de baldosas se puede hacer para aproximar el camino de la curva arbitraria lo más cerca que nos plazca.

Figura 4. Embelado del plano PV con isotermas y adiabatos.

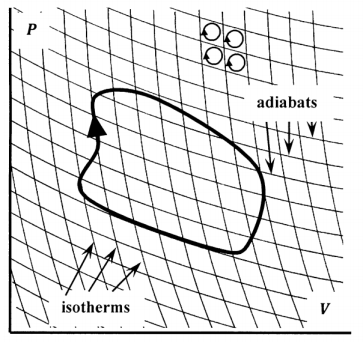
Supongamos que atravesamos el perímetro de cada una de las baldosas individuales en sentido horario, sumando a\(q^{rev}/T\) medida que avanzamos. Los segmentos de estos perímetros se agrupan en dos grupos. Un grupo consta de segmentos que se encuentran en el perímetro del conjunto de baldosas de cerramiento. El otro grupo consta de segmentos que son comunes a dos teselas. Cuando atravesamos ambos mosaicos en el sentido de las agujas del reloj, el segmento compartido se recorre una vez en una dirección y una vez en la otra. Cuando sumamos\(q^{rev}/T\) para estos dos recorridos del mismo segmento, encontramos que la suma es cero, porque tenemos\(q^{rev}/T\) en una dirección y\(-q^{rev}/T\) en la otra. Esto significa que la suma de\(q^{rev}/T\) alrededor de todas las teselas será igual a la suma de\(q^{rev}/T\) alrededor de aquellos segmentos que se encuentran en el perímetro del conjunto de cerramiento. Es decir, tenemos

\[\sum_{ \begin{array}{c} \mathrm{cycle} \\ \mathrm{perimeter} \end{array}} \frac{q^{rev}}{T}+\sum_{ \begin{array}{c} \mathrm{interior} \\ \mathrm{seqments} \end{array}} \frac{q^{rev}}{T}=\sum_{ \begin{array}{c} \mathrm{all} \\ \mathrm{tiles} \end{array}} \left\{\sum_{ \begin{array}{c} \mathrm{tile} \\ \mathrm{perimeter} \end{array}} \frac{q^{rev}}{T}\right\}\]

donde\[\sum_{ \begin{array}{c} \mathrm{interior} \\ \mathrm{seqments} \end{array} } \frac{q^{rev}}{T}=0\]

porque cada segmento interior se recorre dos veces, y las dos contribuciones cancelan exactamente.

Este conjunto de azulejos tiene otra propiedad importante. Dado que cada baldosa individual representa un ciclo reversible de Carnot, sabemos que

\[\sum_{ \begin{array}{c} \mathrm{tile} \\ \mathrm{perimeter} \end{array} }{\frac{q^{rev}}{T}}=0\]

alrededor de cada baldosa individual. Dado que la suma alrededor de cada mosaico es cero, la suma de todas estas sumas es cero. De ello se deduce que la suma de\({q^{rev}}/{T}\) alrededor del perímetro del conjunto envolvente es cero:

\[\sum_{ \begin{array}{c} \mathrm{cycle} \\ \mathrm{perimeter} \end{array} }{\frac{q^{rev}}{T}}=0\]

Al embaldosar el plano de presión-volumen tan densamente como sea necesario, podemos hacer que el perímetro del conjunto de cerramiento sea lo más cercano que queramos a cualquier curva cerrada. Los incrementos de calor se vuelven arbitrariamente pequeños, y

\[\mathop{\mathrm{lim}}_{q^{rev}\to {dq}^{rev}} \left[\sum_{ \begin{array}{c} cycle \\ perimeter \end{array} } \frac{q^{rev}}{T}\right]\ =\oint{\frac{dq^{rev}}{T}}=0\]Para cualquier motor reversible que produzca trabajo a presión y volumen, tenemos\(\oint{dS=0}\) alrededor de cualquier ciclo.

Podemos extender este análisis para llegar a la misma conclusión para un motor reversible que produce cualquier forma de trabajo. Para ver esto, consideremos más cuidadosamente el teorema del mosaico. Cuando decimos que los adiabatos y las isotermas tejan el plano de presión—volumen, queremos decir que cada punto en el plano de presión-volumen está intersectado por uno y solo un adiabat y por una y solo una isoterma. Cuando solo es posible trabajar a presión y volumen, cada punto en el plano de presión-volumen representa un estado único del sistema. Por lo tanto, el teorema del mosaico afirma que cada estado del sistema de presión variable se puede alcanzar a lo largo de uno y solo un adiabat y una y solo una isoterma.

De la experiencia, inferimos que esta afirmación sigue siendo cierta para cualquier forma de trabajo. Es decir, cada estado de cualquier sistema reversible puede ser alcanzado por una y solo una isoterma y por uno y solo un adiabat cuando se realiza alguna forma de trabajo. Si es posible más de una forma de trabajo, hay un adiabat para cada forma de trabajo. Si cambiar\({\theta }_1\) y cambiar\({\theta }_2\) cambian la energía del sistema, los efectos sobre la energía del sistema no son necesariamente los mismos. En general, no\({\mathit{\Phi}}_1\) es lo mismo que\({\mathit{\Phi}}_2\), donde

\[{\mathit{\Phi}}_i={\left(\frac{\partial E}{\partial {\theta }_i}\right)}_{V,{\theta }_{m\neq i}}\]

A partir del § 3, sabemos que un motor Carnot reversible que realiza cualquier forma de trabajo se puede emparejar con un motor Carnot reversible de gas ideal de tal manera que los motores completen los sucesivos pasos isotérmicos y adiabáticos en paralelo. En cada paso, cada motor experimenta los mismos cambios de calor, trabajo, energía y entropía que el otro. Así como podemos trazar el ciclo reversible de Carnot ideal-gas como un camino cerrado en el espacio presión-volumen, podemos trazar un ciclo Carnot produciendo cualquier otra forma de trabajo como un camino cerrado con sucesivos pasos isotérmicos y adiabáticos en\({\mathit{\Phi}}_i{--\theta }_i\) el espacio. Al igual que cualquier camino cerrado en el espacio de presión-volumen se puede embalar (o construir a partir de) ciclos de Carnot reversibles arbitrariamente pequeños, por lo que cualquier camino cerrado en\({\mathit{\Phi}}_i{--\theta }_i\) el espacio puede ser embalado por tales ciclos. Por lo tanto, el argumento que usamos para mostrar que\(\oint{dS=0}\) para cualquier ciclo reversible cerrado en presión-volumen el espacio se aplica igualmente bien a un ciclo reversible cerrado en el que el calor se utiliza para producir cualquier otra forma de trabajo.