9.7: Cambios de entropía para un proceso espontáneo en un sistema aislado

En la Sección 9.6, consideramos los cambios de entropía en un sistema y su entorno cuando el proceso es reversible. Consideramos ahora la situación diametralmente opuesta en la que un sistema aislado sufre un cambio espontáneo. A partir del enunciado basado en entropía de la segunda ley, sabemos cómo cambia la entropía de este sistema y su entorno. Dado que el sistema está aislado, no se produce ningún cambio en los alrededores. Así,\(\Delta \hat{S}=0\); y desde entonces\(\Delta S+\Delta \hat{S}>0\), tenemos\(\Delta S>0\).

Intentemos desarrollar estas conclusiones a partir de la declaración basada en máquinas de la segunda ley. Dado que el proceso ocurre irreversiblemente, no podemos usar el calor del proceso para encontrar el cambio de entropía para el sistema. Podemos calcular el cambio de entropía para un proceso a partir de la ecuación definitoria solo si el proceso es reversible. Sin embargo, la entropía es una función de estado; utilizando la figura del habla que introducimos en la Sección 7.21, podemos encontrar el cambio de entropía para el proceso espontáneo evaluando\(\Delta S\) a lo largo de un segundo camino reversible que conecta los mismos estados inicial y final.

Figura 7. Un ciclo que incluye un proceso espontáneo en un sistema aislado.

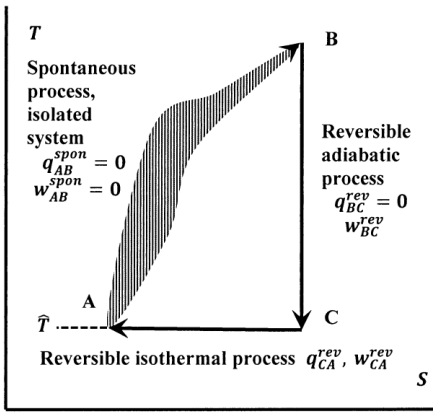
En la Figura 7, estas trayectorias están esquematizadas en el espacio de temperatura-entropía. La transición del estado A al estado B ocurre irreversiblemente, y por lo tanto no necesariamente corresponde a una ruta que podamos especificar en este diagrama. Se supone que la línea discontinua trazada para esta transición nos recuerda este hecho. Podemos diseñar fácilmente un camino reversible de B de regreso a A. Primero, devolvemos reversible y adiabáticamente la temperatura del sistema a su valor original\(\hat{T}\). En este paso, el sistema sí funciona en el entorno, o viceversa. El sistema alcanza el punto C del diagrama. Después agregamos o retiramos de manera reversible e isotérmica calor del sistema para volver al estado original en el punto A. Para que la transferencia de calor sea reversible, debemos tener\(T=\hat{T}\) para este paso. De ahí que la temperatura final (y original) del sistema en el punto A sea igual a la temperatura del entorno. El camino reversible\(B\to C\to A\) debe existir, porque el teorema del mosaico afirma que los adiabatos (líneas verticales) y las isotermas (líneas horizontales)\(T--S\) tejan el plano arbitrariamente densamente.

Tomada literalmente, esta descripción del estado A es inconsistente. Suponemos que el estado inicial A es capaz de un cambio espontáneo; por lo tanto, no puede ser un estado de equilibrio. Suponemos que el estado final A se alcanza mediante un proceso reversible; por lo tanto, debe ser un estado de equilibrio. Puentamos esta contradicción refinando nuestra definición del estado inicial. El estado final A es un estado de equilibrio con funciones de estado bien definidas. Lo que tenemos en mente es que estos valores finales de equilibrio-estado también caracterizan el estado inicial de no equilibrio. Evidentemente, el estado inicial A que tenemos en mente es un estado hipotético. Este estado hipotético se aproxima al estado de un sistema real que sufre un cambio espontáneo. Al invocar este hipotético estado inicial, eliminamos la contradicción entre nuestras descripciones del estado inicial A y el estado final A. Dado un sistema real que sufre un cambio espontáneo, debemos encontrar valores aproximados para las funciones estatales del sistema real encontrando un equilibrio —o cuasi-equilibrio— sistema que modele adecuadamente el estado inicial del sistema que cambia espontáneamente.

En el desarrollo a continuación, no ponemos restricciones sobre la naturaleza del sistema o el proceso espontáneo. Suponemos que las funciones estatales de cualquier estado inicial hipotético A pueden aproximarse adecuadamente mediante algún modelo de estado de equilibrio. No obstante, antes de considerar el argumento general, mostremos cómo se pueden cumplir estas condiciones para otro sistema específico. Considera una vasija cuyo interior está dividido por una partición. El gas real de una sustancia pura ocupa el espacio en un lado de la partición. Se evacua el espacio del otro lado de la partición. Suponemos que esta vasija está aislada. El gas real está en equilibrio. Podemos medir sus funciones de estado, incluyendo su presión, volumen y temperatura. Ahora supongamos que pinchamos la partición. Tan pronto como lo hacemos, el gas se expande espontáneamente para llenar todo el recipiente, alcanzando una nueva posición de equilibrio, a una nueva presión, volumen y temperatura. El gas experimenta una expansión libre, tal como se define en la Sección 7.17.

En el instante en que se perfora la partición, el sistema se vuelve capaz de sufrir un cambio espontáneo. En este hipotético estado inicial, antes de que cualquier cantidad significativa de gas pase por la abertura, ni la condición real del gas ni los valores de sus funciones de estado han cambiado. Después de la expansión al nuevo estado de equilibrio, el estado original puede restaurarse mediante procesos reversibles de compresión adiabática y ajuste de volumen isotérmico. (Los problemas 13 y 14 del Capítulo 10 tratan de los cambios de energía y entropía para gases ideales y reales alrededor de un ciclo en el que la expansión espontánea en un sistema aislado es seguida por la restauración reversible del estado inicial.)

Volviendo al ciclo general representado en la Figura 7, vemos que existen algunas condiciones importantes sobre los términos de calor y trabajo en los pasos individuales. Dado que el sistema está aislado mientras experimenta la transición de A a B, no intercambia calor ni trabaja con el entorno en este paso:\(q^{spon}_{AB}=w^{spon}_{AB}=0\). Para la transición adiabática reversible de B a C,\(d_{BC}q^{rev}=0\) en cada parte incremental del camino. La transición de C a A ocurre de manera reversible e isotérmica; dejando que el calor de este paso sea\(q^{rev}_{CA}\), los cambios de entropía para estos pasos reversibles son, a partir de la ecuación definitoria,

\[{\Delta }_{BC}S=\int^{T_C}_{T_B}{\frac{d_{BC}q^{rev}}{T}}=0\]y\[{\Delta }_{CA}S=\frac{q^{rev}_{CA}}{\hat{T}}\]

Los cambios de energía y entropía alrededor de este ciclo deben ser cero, ya sea que los pasos individuales ocurran de manera reversible o irreversible. Tenemos

\[\Delta E=q^{spon}_{AB}+w^{spon}_{AB}+q^{rev}_{BC}+w^{rev}_{BC}+q^{rev}_{CA}+w^{rev}_{CA}=q^{rev}_{CA}+w^{rev}_{BC}+w^{rev}_{CA}=0\]y

\[\Delta S={\Delta }_{AB}S+{\Delta }_{BC}S+{\Delta }_{CA}S ={\Delta }_{AB}S+{q^{rev}_{CA}}/{\hat{T}}=0\]

Queremos analizar este ciclo utilizando el enunciado basado en máquinas de la segunda ley. Tenemos\(w^{rev}_{BC}=-{\hat{w}}^{rev}_{BC}\),\(w^{rev}_{CA}=-{\hat{w}}^{rev}_{CA}\), y\(q^{rev}_{CA}=-{\hat{q}}^{rev}_{CA}\). Supongamos que el sistema hace trabajo neto en el entorno a medida que este ciclo se recorre así\({\hat{w}}^{rev}_{BC}+{\hat{w}}^{rev}_{CA}>0\). Entonces,

\[-\left({\hat{w}}^{rev}_{BC}+{\hat{w}}^{rev}_{CA}\right)=w^{rev}_{BC}+w^{rev}_{CA}<0\]

y de ello se deduce\(q^{rev}_{CA}>0\). El sistema intercambia calor con el entorno en un solo paso de este proceso. En este paso, el sistema extrae una cantidad de calor de un reservorio en los alrededores. La temperatura de este reservorio permanece constante durante\(\hat{T}\) todo el proceso. El calor extraído por el sistema se convierte completamente en trabajo. Este resultado contradice la afirmación basada en máquinas de la segunda ley. Por lo tanto,\(w^{rev}_{BC}+w^{rev}_{CA}<0\) es falso; de ello se deduce que

\[w^{rev}_{BC}+w^{rev}_{CA}\ge 0\]

y que\[q^{rev}_{CA}\le 0\]

Para el cambio de entropía en el proceso espontáneo en el sistema aislado, tenemos

\[{\Delta }_{AB}S=-{q^{rev}_{CA}}/{\hat{T}}\ge 0\]

Ahora, introducimos la premisa de que\(q^{rev}_{CA}\neq 0\). Si esto es cierto, el cambio de entropía en el proceso espontáneo en el sistema aislado se convierte en

\[{\Delta }_{AB}S>0\]

(Lo contrario también es cierto; es decir,\({\Delta }_{AB}S>0\) implica que\(q^{rev}_{CA}\neq 0\).) La premisa que\(q^{rev}_{CA}\neq 0\) es independiente de la declaración basada en máquinas de la segunda ley, que sólo requiere eso\(q^{rev}_{CA}\le 0\), como acabamos de demostrar. También es independiente de la primera ley, que sólo requiere eso\(q^{rev}_{CA}=-w^{rev}_{BC}-w^{rev}_{CA}\). Si\(q^{rev}_{CA}\neq 0\), podemos concluir que, para un proceso espontáneo en un sistema aislado, debemos tener\(w_{BC}+w_{CA}>0\) y\(q^{rev}_{CA}<0\). Estas condiciones corresponden a hacer trabajos en el sistema y encontrar que el calor es liberado por el sistema. No hay objeción a esto; es posible convertir la energía mecánica en calor cuantitativamente. Las conclusiones que\(q^{rev}_{CA}<0\) y\({\Delta }_{AB}S>0\) tienen consecuencias importantes; las consideramos a continuación. Primero, sin embargo, consideramos una línea de pensamiento que nos lleva a inferir eso\(q^{rev}_{CA}\neq 0\) y de ahí que eso\(q^{rev}_{CA}<0\) debe ser cierto.

Porque\(q_{AB}=0\) y\(w_{AB}=0\), tenemos\({\ E}_A=E_B\). El sistema puede ser tomado del estado A al estado B por el proceso reversible\(\to C\to B\) A. Arriba vemos que si\(q^{rev}_{CA}=0\), tenemos\({\ S}_A=S_B\). En § 6-10, introducimos el teorema de Duhem, que afirma que dos variables termodinámicas son suficientes para especificar el estado de un sistema reversible cerrado en el que solo es posible el trabajo presión-volumen. Damos una prueba del teorema de Duhem cuando las dos variables se eligen de entre las variables de presión, temperatura y composición que describen el sistema. Se evitó especificar si se pueden usar otros pares de variables. Si asumimos ahora que especificar las variables energía y entropía siempre es suficiente para especificar el estado de dicho sistema, se deduce que los estados A y B deben de hecho ser el mismo estado. (En el § 14, y con mayor detalle en el capítulo 10, vemos que la primera ley y nuestra declaración de la segunda ley basada en entropía implican efectivamente que especificar la energía y la entropía especifica el estado de un sistema reversible cerrado en el que solo es posible el trabajo de presión-volumen).

Si el estado A y el estado B son el mismo estado; es decir, si las funciones de estado del estado A son las mismas que las del estado B, no tiene sentido decir que hay un proceso espontáneo que convierte el estado A en estado B. Por lo tanto, si A puede convertirse a B en un proceso espontáneo en un sistema aislado, debe ser eso\(q^{rev}_{CA}\neq 0\). Es decir,

\[\left[\left(q^{rev}_{CA}=0\right)\Rightarrow \sim \left(\mathrm{A\ can\ go\ to\ B\ spontaneously}\right)\right]\]\[\Rightarrow \left[\left(A\ \mathrm{can\ go\ to\ B\ spontaneously}\right)\Rightarrow \left(q^{rev}_{CA}\neq 0\right)\right]\]

De la declaración basada en máquinas de la segunda ley, encontramos\({\Delta }_{AB}S=-{q^{rev}_{CA}}/{\hat{T}}\ge 0\). Cuando complementamos esta conclusión con nuestra inferencia basada en el teorema de Duhem de que\(q^{rev}_{CA}\neq 0\), podemos concluir que\(\Delta S>0\) para cualquier proceso espontáneo en cualquier sistema aislado. Porque el sistema está aislado, tenemos\(\hat{q}=0\), y\(\Delta \hat{S}=0\). Para cualquier proceso espontáneo en cualquier sistema aislado tenemos

\[\Delta S_{universe}=\Delta S+\Delta \hat{S}>0.\]

También podemos concluir que lo contrario es cierto; es decir, si\({\Delta }_{AB}S=S_B-S_A>0\) para un proceso en el que un sistema aislado va del estado A al estado B, el proceso debe ser espontáneo. Dado que cualquier proceso que ocurra en un sistema aislado debe ser un proceso espontáneo, sólo es necesario demostrar que eso\({\Delta }_{AB}S>0\) implica que el estado B es diferente del estado A. Esto es trivial. Debido a que la entropía es una función de estado,\(S_B-S_A>0\) requiere que el estado B sea diferente del estado A.

Ninguno de nuestros argumentos depende de la magnitud del cambio que se produzca. Evidentemente, la misma desigualdad debe describir cada porción incremental de cualquier proceso espontáneo; de lo contrario, podríamos definir un cambio espontáneo incremental para el cual se violaría la declaración basada en máquinas de la segunda ley. Por cada parte incremental de cualquier cambio espontáneo en cualquier sistema aislado tenemos\(dS>0\) y

\[dS_{universe}=dS+d\hat{S}>0.\]

Estos son resultados de importancia fundamental; exploramos sus ramificaciones a continuación. Antes de hacerlo, sin embargo, volvamos a considerar un sistema en el que solo es posible trabajar a presión y volumen. Existe una forma alternativa de expresar la idea de que tal sistema está aislado. Dado que un sistema aislado no puede interactuar de ninguna manera con su entorno, no puede intercambiar energía con su entorno. Su energía debe ser constante. Dado que no puede intercambiar trabajo de presión-volumen, su volumen debe ser constante. De ahí que el aislamiento implica constante\(E\) y\(V\). Si solo es posible el trabajo a presión y volumen, lo contrario debe ser cierto; es decir, si solo es posible el trabajo a presión y volumen, la energía constante y el volumen implican que no hay interacciones entre el sistema y su entorno. Por lo tanto, constante\(E\) e\(V\) implica que el sistema está aislado, y debe ser cierto eso\(\Delta \hat{S}=0\). En este caso, un proceso espontáneo en el que\(E\) y\(V\) son constantes debe ir acompañado de un incremento en la entropía del sistema. (Si\(V\) es constante y solo es posible el trabajo a presión y volumen, el proceso no implica trabajo). Tenemos un criterio para el cambio espontáneo:

\[{\left(\Delta S\right)}_{EV}>0\](proceso espontáneo, solo trabajo de presión-volumen)

donde los subíndices indican que la energía y el volumen del sistema son constantes. (En la Sección 9.21, llegamos a esta conclusión por un argumento diferente.)