9.15: Entropía y Cambio Espontáneo

En un proceso reversible, los cambios que ocurren en el sistema son impuestos por el entorno; el cambio reversible ocurre sólo porque el sistema responde a cambios en las condiciones que le imponen su entorno. Un proceso reversible es impulsado por el entorno. En contraste, un proceso espontáneo es impulsado por el sistema. Sin embargo, cuando ocurre un proceso espontáneo bajo algún conjunto específico de condiciones impuestas (valores específicos de temperatura y presión, por ejemplo) el estado de equilibrio del sistema depende de estas condiciones. Para especificar un cambio espontáneo particular, debemos especificar suficientes restricciones para fijar el estado final del sistema.

Para ver estos puntos desde una perspectiva ligeramente diferente, consideremos un sistema reversible cerrado en el que solo es posible trabajar a presión y volumen. El teorema de Duhem afirma que un cambio en el estado de este sistema puede especificarse especificando los cambios en algún par de funciones de estado, digamos\(X\) y\(Y\). Si los valores impuestos de\(X\) y\(Y\) son constantes en sus valores de equilibrio eventuales, pero el sistema está cambiando, el sistema no puede estar en un colector de equilibrio gibbsiano. Decimos que el sistema está experimentando un cambio espontáneo a constante\(\ X\) y\(Y\).

Esta descripción es una figura de discurso en que los\(Y\) valores del sistema\(X\) y no necesariamente alcanzan los valores impuestos y se vuelven constantes hasta alcanzar el equilibrio. Un ejemplo está en orden: Un sistema cuya presión y temperatura originales son\(P_i\) y\(T_i\) pueden sufrir un cambio espontáneo mientras que el entorno impone una presión constante,\(P_{applied}=P_f\), y el sistema se sumerge en baño de temperatura constante a\(T=T_f\). La presión y temperatura del sistema pueden ser indeterminadas a medida que ocurre el proceso, pero la presión y temperatura de equilibrio deben ser\(P_f\) y\(T_f\).

Si el entorno opera para imponer valores particulares de\(\boldsymbol{X}\) y\(\boldsymbol{Y}\) sobre el sistema, entonces la posición en la que el sistema finalmente alcanza el equilibrio está determinada por estos valores. Se alcanza el mismo estado de equilibrio para cualquier elección de entorno que imponga los mismos valores de\(\boldsymbol{X}\) y\(\boldsymbol{Y}\) sobre el sistema en el momento en que el sistema alcanza el equilibrio. Por cada forma adicional de trabajo sin presión-volumen que afecte al sistema, debemos especificar el valor de una variable adicional para especificar un estado de equilibrio único.

Los cambios de entropía que ocurren en el sistema y su entorno durante un proceso espontáneo tienen valor predictivo. Sin embargo, nuestras definiciones no nos permiten encontrar el cambio de entropía para un proceso espontáneo, y la temperatura del sistema puede no tener un valor significativo. Por otro lado, siempre podemos llevar a cabo el proceso para que la temperatura de los alrededores se conozca en cada punto del proceso. En efecto, si el sistema está en contacto térmico con su entorno a medida que ocurre el proceso, no podemos especificar las condiciones bajo las cuales se produce el proceso sin especificar la temperatura del entorno a lo largo de este camino.

En la Figura 9 se describe un proceso espontáneo cuya trayectoria puede especificarse por los valores de la variable termodinámica\(Y\) y la temperatura del entorno\(\hat{T}\), en función del tiempo\(t\). Denotemos como la curva que describe este camino\(C\). Podemos dividir este camino en intervalos cortos. Dejar\(C_k\) denotar un segmento corto de esta trayectoria a lo largo del cual la temperatura de los alrededores es aproximadamente constante. Para nuestros propósitos actuales, la temperatura del sistema,\(T\), es irrelevante; dado que el proceso es espontáneo, la temperatura del sistema puede no tener valor significativo dentro del intervalo\(C_k\). A medida que el sistema atraviesa segmento\(C_k\), acepta una cantidad de calor\(q_k\),, del entorno, que están a temperatura\({\hat{T}}_k\). El calor intercambiado por los alrededores dentro\(C_k\) es\({\hat{q}}_k=-q_k\). A continuación, mostramos que siempre es posible llevar a cabo el proceso de tal manera que el cambio en el entorno se produzca de manera reversible. Entonces

\[\Delta {\hat{S}}_k=\frac{{\hat{q}}_k}{{\hat{T}}_k}=-\frac{q_k}{{\hat{T}}_k}\]

y puesto que\(\Delta S_k+\Delta {\hat{S}}_k>0\), de ello se deduce que

\[\Delta S_k>\frac{q_k}{{\hat{T}}_k}\]

Esta es la desigualdad de Clausius. Desempeña un papel central en la termodinámica de los procesos espontáneos. Cuando hacemos los intervalos\(C_k\) arbitrariamente cortos, tenemos

\[dS_k>\frac{{dq}_k}{{\hat{T}}_k}\]

Para demostrar que podemos medir el cambio de entropía en el entorno durante un proceso espontáneo, utilicemos un dispositivo conceptual para transferir el calor\(q_k\), que debe intercambiarse del entorno\(\hat{T}_k\) a temperatura, al sistema. Como se esboza en la Figura 10, imaginamos un motor Carnot muy pequeño, reversible, de gas ideal, cuyo depósito de alta temperatura también es muy pequeño. Suponemos que el motor Carnot entrega un incremento de calor muy pequeño\(\delta q\) al depósito de alta temperatura en cada ciclo. Mientras el sistema está dentro\(C_k\), mantenemos el depósito de alta temperatura del motor Carnot en\(\hat{T}_k\), y permitimos que el calor\(q_k\) pase del depósito de alta temperatura al sistema. El reservorio de alta temperatura es la única parte del entorno que está en contacto térmico con el sistema;\(q_k\) es el único calor intercambiado por el sistema mientras está dentro\(C_k\).

Figura 10. Usar un motor Carnot reversible para intercambiar calor con un sistema que cambia espontáneamente.

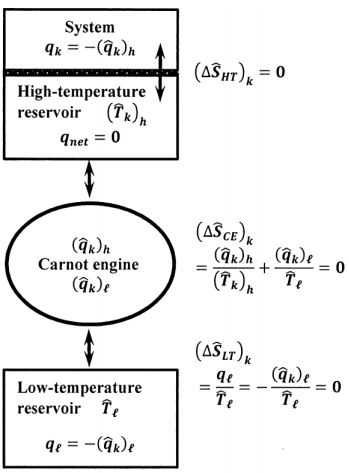
Para mantener el depósito de alta temperatura en\({\hat{T}}_k\) operamos el motor Carnot durante un gran número integral de ciclos,\(n\), de tal manera que\(q_k\approx n\times \delta q\), y lo hacemos a una velocidad que solo coincide con la velocidad a la que el calor pasa del depósito de alta temperatura al sistema. Cuando el sistema pasa de segmento de trayectoria\(C_k\) a segmento de trayectoria\(C_{k+1}\), alteramos los pasos en el ciclo reversible de Carnot para mantener el reservorio de alta temperatura a la nueva temperatura del entorno,\({\hat{T}}_{k+1}\). El depósito de calor a baja temperatura para este motor Carnot está siempre a la temperatura constante\({\hat{T}}_{\ell }\). Deje que el calor entregado desde el depósito de alta temperatura al motor Carnot dentro\(C_k\) sea\({\left({\hat{q}}_k\right)}_h\). Tenemos\(q_k=-{\left({\hat{q}}_k\right)}_h\). Deje que el calor entregado desde el depósito de baja temperatura al motor Carnot dentro\(C_k\) sea\({\left({\hat{q}}_k\right)}_{\ell }\). Deje que el calor entregado al depósito de baja temperatura dentro\(C_k\) sea\(q_{\ell }\). Tenemos\(q_{\ell }=-{\left({\hat{q}}_k\right)}_{\ell }\). Como el motor Carnot es reversible, tenemos

\[\frac{\left(\hat{q}_k\right)_h}{\hat{T}_k}+\frac{\left( \hat{q}_k\right)_{\ell }}{\hat{T}_{\ell }}=0\]

y

\[-\frac{q_k}{\hat{T}_k}-\frac{q_{\ell }}{\hat{T}_{\ell }}=0\]

para que

\[\frac{q_{\ell }}{\hat{T}_{\ell }}=-\frac{q_k}{\hat{T}_k}\]

Mientras el sistema está dentro\(C_k\), recibe un incremento de calor\(q_k\) del depósito de alta temperatura. Simultáneamente, tres componentes en los alrededores también intercambian calor. Deje que los cambios de entropía en el depósito de alta temperatura, el motor Carnot y el depósito de baja temperatura sean\({\left(\Delta {\hat{S}}_{HT}\right)}_k\)\({\left(\Delta {\hat{S}}_{CE}\right)}_k\), y\({\left(\Delta {\hat{S}}_{LT}\right)}_k\), respectivamente. El depósito de alta temperatura recibe calor\(q_k\) del motor Carnot y entrega la misma cantidad de calor al sistema. El calor neto aceptado por el reservorio de alta temperatura es cero. No se producen cambios en el depósito de alta temperatura. Tenemos\({\left(\Delta {\hat{S}}_{HT}\right)}_k=0\). El motor reversible Carnot completa un número integral de ciclos, así que eso\({\left(\Delta {\hat{S}}_{CE}\right)}_k=0\). El depósito de baja temperatura acepta calor\({-\left({\hat{q}}_k\right)}_{\ell }=q_{\ell }\), a temperatura fija\({\hat{T}}_{\ell }\), durante el funcionamiento reversible del motor Carnot, de manera que

\[\left(\Delta \hat{S}_{LT}\right)_k=\frac{q_{\ell }}{\hat{T}_{\ell }}=-\frac{q_k}{\hat{T}_k}\]

El cambio de entropía en el entorno a medida que pasa el sistema\(C_k\) es

\[\Delta \hat{S}_{k}= \left(\Delta \hat{S}_{HT}\right)_k+ \left(\Delta \hat{S}_{CE}\right)_k+\left(\Delta \hat{S}_{LT}\right)_k=\frac{q_{\ell }}{\hat{T}_{\ell }}=-\frac{q_k}{\hat{T}_k}\]

de manera que, como observamos anteriormente,

\[\Delta S_k >- \Delta {\hat{S}}_k =\frac{q_k}{\mathrm{\ }{\hat{T}}_k}\]

Dado que\(C_k\) puede ser cualquier parte del camino C, y\(C_k\) puede hacerse arbitrariamente corto, tenemos por cada incremento de cualquier proceso espontáneo que ocurra en un sistema cerrado que pueda intercambiar calor con su entorno,\(d\hat{S}=-{dq}/{\hat{T}}\), y

\[dS>\frac{dq}{\hat{T}}\]

Si la temperatura de los alrededores es constante entre dos puntos A y B cualesquiera en la curva C, podemos integrar a lo largo de este intervalo para obtener\(\mathrm{\Delta }_{\mathrm{AB}}\widehat{\mathrm{S}}\mathrm{=-} \mathrm{q}_{\mathrm{AB}}/\widehat{\mathrm{T}}\) y

\[\mathrm{\Delta }_{\mathrm{AB}}\mathrm{S>}\frac{\mathrm{q}_{\mathrm{AB}}}{\widehat{\mathrm{T}}}\]

Para un proceso adiabático,\(q=0\). Para cualquier incremento arbitrariamente pequeño de un proceso adiabático,\(dq=0\). De ello se deduce que\(\Delta S>0\) y\(dS>0\) para cualquier proceso adiabático espontáneo.