10.2: dE = TDs - PdV y consistencia interna
- Page ID
- 74539
En el Capítulo 1, observamos que el negocio de la ciencia es la creación de modelos que sean internamente consistentes y que describan con precisión la realidad. La deducción lógica de hipótesis tentativas es una herramienta valiosa en nuestro esfuerzo por crear nuevos modelos. Tales argumentos lógicos a menudo toman la forma de “experimentos Gedanken (pensamiento)”, como lo ejemplifican nuestros diversos argumentos sobre las propiedades de los hipotéticos motores de pistón libres de fricción. Sin embargo, la ruta por la que llegamos a una teoría es irrelevante; lo que cuenta es la consistencia interna y la capacidad predictiva de la teoría. Hagamos una pausa, pues, para señalar que hemos llegado a expresiones matemáticas de ideas que inicialmente introdujimos como principios inferidos de la experiencia.
En el Capítulo 6, probamos el teorema de Duhem cuando las variables se eligen entre la presión establecida, la temperatura, el volumen y las concentraciones de componentes. Sin embargo, el teorema es más general. Afirma que dos variables son suficientes para especificar cambios en el estado de un sistema cerrado y reversible, en el que sólo es posible el trabajo presión-volumen. Nuestras derivaciones nos han llevado ahora a la conclusión de que la energía de dicho sistema puede expresarse en función de la entropía y el volumen. Dada la entropía, el volumen y la función\(E = E\left(S,V\right)\), las relaciones desarrolladas anteriormente significan que sabemos\(S\),\(V\),\(E\),\(P\), y\(T\) para el sistema. Dados estos, podemos calcular\(H\),\(A\), y\(G\). Es decir, especificar los cambios en las dos variables\(S\) y\(V\) es suficiente para especificar el cambio en el estado del sistema. Además, podemos reorganizar la ecuación fundamental para
\[dV = \left(\frac{T}{P}\right)dS + \left(\frac{\mathrm{1}}{P}\right)dE\]
para que el volumen pueda expresarse en función de la entropía y la energía. Dado\(S\),\(E\), y la función\(V = V\left(S,E\right)\), podemos encontrar\(P\) y\(T\). Especificar los cambios en\(S\) y\(E\) es suficiente para especificar el cambio en el sistema. Finalmente, podemos reorganizar la ecuación fundamental para
\[dS = \left(\frac{\mathrm{1}}{T}\right)dE + \left(\frac{P}{T}\right)dV\]
de manera que\(S = S\left(V,E\right)\) y especificando cambios en\(E\) y\(V\) es suficiente para especificar el cambio en el sistema.
Ahora, volvamos a nuestra discusión en la Sección 9.7 del cambio de entropía para un sistema aislado que experimenta un cambio espontáneo. Esa discusión explora el uso de la afirmación basada en máquinas de la segunda ley para establecer que la entropía de un sistema aislado debe aumentar durante cualquier proceso espontáneo. Para inferir que la entropía del sistema debe incrementarse en tal proceso, consideramos el caso especial en el que solo es posible el trabajo de presión-volumen y argumentamos que un cambio en el que no\(\mathrm{\Delta }E = \mathrm{\Delta }S\mathrm{=0}\) hay ningún cambio en absoluto. Es decir, suponemos que especificar el cambio en\(E\) y\(S\) es suficiente para especificar el cambio en el estado de dicho sistema. Se trata, por tanto, de un importante control de la consistencia interna de nuestro modelo termodinámico para ver que eso\(dE = TdS + PdV\) implica\(E\) y de hecho\(S\) son un par suficiente.
Finalmente, consideremos la relación de un proceso espontáneo en un sistema cerrado con la superficie que describe procesos reversibles en un mismo sistema. La energía del sistema que experimenta un cambio reversible se expresa como\(E = E\left(S,V\right)\). En la Figura 1 se esboza una superficie de energía en el\(V-S-E\) espacio. En cualquier punto de esta superficie, el sistema está en equilibrio. El punto\(\left(V_0,S_0,E_0\right)\) es tal punto. La tangente a esta superficie en\(\left(V_0,S_0,E_0\right)\) y en el plano\(V = V_0\) es la derivada parcial\(T = {\left({\partial E}/{\partial S}\right)}_V\). La tangente a la superficie en\(\left(V_0,S_0,E_0\right)\) y en el plano\(S = S_0\) es la derivada parcial\(P\mathrm{=-}{\left({\partial E}/{\partial V}\right)}_S\).
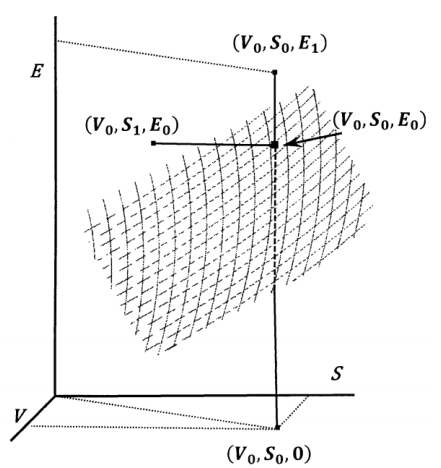
Ningún punto en el\(V-S-E\) espacio que esté fuera de la\(E = E\left(S,V\right)\) superficie puede describir un estado de equilibrio del sistema cerrado. En la práctica, algunos de estos puntos pueden representar estados que el sistema puede alcanzar. Si es así, son estados transitorios de un sistema que cambia espontáneamente. Supongamos, por ejemplo, que somos capaces de
mantener\(S = S_0\) y\(V = V_0\) mientras se produce una reacción química lenta en el sistema. En cada instante, dicho estado debe tener una composición de no equilibrio. Debe tener una energía, y esta energía debe superar\(E_0\); ya que debemos tener\({\left(\mathrm{\Delta }E\right)}_{SV}\mathrm{<0}\) para un proceso espontáneo, un punto\(\left(V_0,S_0,E_{\mathrm{1}}\right)\) puede representar un estado del sistema durante un cambio espontáneo sólo si\(E_{\mathrm{1}}\mathrm{>}E_0\). Si\(E_{\mathrm{2}}\mathrm{<}E_0\), el punto\(\left(V_0,S_0,E_{\mathrm{2}}\right)\) no puede representar un estado del sistema que pueda ir espontáneamente al equilibrio\(\left(V_0,S_0,E_0\right)\). De igual manera, si\(S_{\mathrm{1}}\mathrm{<}S_0\) y el sistema se aísla con\(E = E_0\) y\(V = V_0\), el punto\(\left(V_0,S_{\mathrm{1}},E_0\right)\) representa un estado del sistema que puede ir al equilibrio en\(\left(V_0,S_0,E_0\right)\) forma espontánea. Este proceso satisfaría el criterio de entropía,\({\left(\mathrm{\Delta }S\right)}_{EV}\mathrm{>0}\).


