10.8: Uso del Par (V, P) o el Par (T, S) como Variables Independientes
- Page ID
- 74545
Cuando solo es posible trabajar a presión y volumen, varios pares de funciones de estado pueden especificar el estado de cualquier sistema de equilibrio cerrado. Un par dado puede ser suficiente para especificar el estado en un colector Gibbsiano dado pero no para especificar el estado del mismo sistema en un colector Gibbsiano diferente. (En la Sección 10.7, vemos que el conjunto\(\left\{T,P\right\}\) es suficiente para especificar el estado de un sistema cerrado que contiene solo agua líquida o solo agua gaseosa. Sin embargo, especificar T y P no es suficiente para establecer la cantidad de vapor de agua en un sistema cerrado en el que el líquido se vaporiza reversiblemente).
También puede suceder que un par dado de funciones de estado especifique el estado de un sistema cerrado sobre una parte pero no la totalidad de un colector gibbsiano dado. Especificar los valores de dicho par no es suficiente para describir todo el colector. En particular, podemos demostrar que ni el set\(\left\{P,V\right\}\) ni el conjunto\(\left\{T,S\right\}\) son siempre un par suficiente en este sentido.
Cuando decimos que especificar\(P\) y\(V\) es suficiente para especificar el estado de un sistema en un colector gibbsiano particular, nos referimos a que cualquier función de estado,\(M\), debe especificarse de manera única cuando\(P\) y\(V\) se especifican; una función de un solo valor\(M\left(P,V\right)\),, debe existir. Por el contrario, si para cualquier elección de\(M\) en cualquier sistema, no\(M\left(P,V\right)\) es de un solo valor,\(\ P\) y no siempre\(V\) son un conjunto suficiente. En el § 6, vemos cómo encontrar el diferencial total,\[dM={\left(\frac{\partial M}{\partial P}\right)}_VdP+{\left(\frac{\partial M}{\partial V}\right)}_PdV\]
Podría parecer que esto es suficiente para asegurar que especificar P y V siempre nos permita encontrar\(M\left(P,V\right)\) relativo a su valor en un estado de referencia inicial\(M\left(P_1,V_1\right)\). Para ello, solo necesitamos evaluar\(dM\) como una línea integral a lo largo de algún camino reversible que nos lleve de\(\left(P_1,V_1\right)\) a\(\left(P_2,V_2\right)\). Sin embargo, podemos evaluar esta línea integral solo si se pueden integrar ambas derivadas parciales. Si una de las derivadas parciales está indefinida a lo largo de cualquier ruta que se conecte\(\left(P_1,V_1\right)\) a\(\left(P_2,V_2\right)\), no podemos encontrar\(M\left(P,V\right)\) por este método.
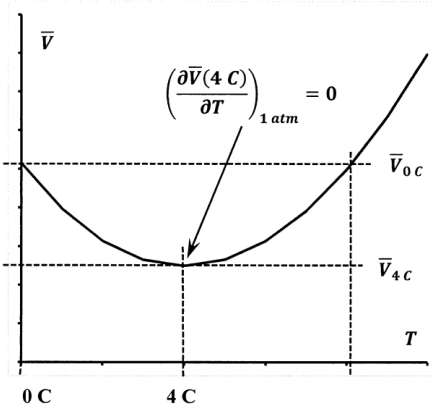
Consideremos un sistema reversible cerrado que consiste en un mol de agua líquida. A presiones ordinarias, la densidad del agua líquida no es una función monótona de la temperatura. A una atmósfera, la densidad del agua líquida alcanza un máximo a 4 C. Por lo tanto, a una presión de una atmósfera, el volumen molar de agua es mínimo a 4 C, como se indica en la Figura 2. Esto significa que, a una atmósfera y un rango de volúmenes, el agua líquida puede estar a cualquiera de dos temperaturas para valores especificados de\(P\) y\(\overline{V}\). Por lo tanto, especificando\(P\) y\(\overline{V}\) no especifica\(T\); la temperatura no es una función de valor único de presión y volumen; no podemos expresar de manera única la temperatura como la función requerida\(T=T\left(P,\overline{V}\right)\). Además, debido a que la densidad tiene un máximo, tenemos
\[{\left(\frac{\partial \overline{V}}{\partial T}\right)}_P=0\]
a este máximo, y de ello se deduce que
\[{\left(\frac{\partial T}{\partial \overline{V}}\right)}_P\]
no se define a esta temperatura y presión. En la Sección 10.6, encontramos
\[{\left(\frac{\partial \overline{S}}{\partial \overline{V}}\right)}_P={\frac{C_P}{T}\left(\frac{\partial T}{\partial \overline{V}}\right)}_P\]así que eso también\({\left({\partial \overline{S}}/{\partial \overline{V}}\right)}_P\) está indefinido. Por lo tanto, no podemos evaluar\(\Delta \overline{S}\) evaluando la integral de línea\(d\overline{S}\left(P,\overline{V}\right)\) a lo largo de ningún camino que incluya un punto de densidad máxima. Estos ejemplos muestran que la presión y el volumen no son suficientes para describir todo el colector Gibbsiano para agua líquida.
La temperatura y la entropía tampoco son suficientes. Ya que tenemos
\[d\overline{S} = \frac{C_P}{T}dT + {\left(\frac{\partial \overline{V}}{\partial T}\right)}_PdP\]
el diferencial total para la presión en función de la entropía y la temperatura es
\[dP = \left[\frac{C_P}{T}dT + d\overline{S}\right]{\left(\frac{\partial T}{\partial \overline{V}}\right)}_P\]
de manera que no\(dP\) se define a presiones y temperaturas de máxima densidad. En consecuencia, no podemos expresar la presión como\(P=P\left(\overline{S},T\right)\) sobre toda la región líquida.


