10.14: El efecto Joule-Thomson

En la práctica, el experimento de Joule-Thomson se realiza permitiendo que el gas de un recipiente a presión pase a través de un tubo aislado. El tubo contiene una válvula de estrangulación o un tapón poroso a través del cual el gas fluye lo suficientemente lento para que el gas aguas arriba del tapón esté a una presión uniforme\(P_{\mathrm{1}}\), y el gas aguas abajo esté a una presión uniforme\(P_{\mathrm{2}}\). En general, la temperatura del gas aguas abajo es diferente de la del gas aguas arriba. Dependiendo de la temperatura y presión iniciales, la caída de presión y el gas, la temperatura del gas puede disminuir o aumentar a medida que pasa a través del tapón. (A continuación vemos que debe ser constante si el gas es ideal.)

El cambio de temperatura se llama efecto Joule-Thomson. La entalpía del gas permanece constante. Si los cambios de temperatura y presión medidos son\(\mathrm{\Delta }T\) y\(\mathrm{\Delta }P\), su relación se llama el coeficiente de Joule-Thomson,\({\mu }_{JT}\). Definimos

\[\mathrm{\ }{\mu }_{JT} = {\left(\frac{\partial T}{\partial P}\right)}_H\mathrm{\approx }\frac{\mathrm{\Delta }T}{\mathrm{\Delta }P}\]

Figura 3. El experimento idealizado de Joule-Thomson

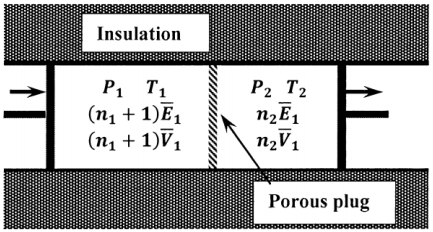
Para ver que la entalpía del gas es la misma en ambos lados del tapón, consideramos una versión idealizada del experimento, en la que el flujo de gas a través del tapón es controlado por el movimiento coordinado de dos pistones. (Ver Figura 3.) Suponemos que el gas es empujado a través del tapón de tal manera que la presión aguas arriba permanece constante en\(P_1\) y la presión aguas abajo permanece constante en\(P_2\). Consideremos los cambios que resultan cuando un mol de gas pasa por el tapón bajo estas condiciones. Inicialmente, hay\(n_1+1\) moles de gas en el lado aguas arriba a una presión\(P_1\), ocupando un volumen\(\left(n_1+1\right){\overline{V}}_1\), a una temperatura\(T_1\), y teniendo una energía por mol de\({\overline{E}}_1\). En el lado aguas abajo, hay\(n_2\) moles de gas a una presión\(P_2\), ocupando un volumen\(n_2{\overline{V}}_2\), pero teniendo una temperatura\(T_2\) y una energía por mol de\({\overline{E}}_2\).

Cuando se completa el proceso, hay\(n_1\) moles de gas en el lado aguas arriba, aún a presión\(P_1\) y temperatura\(T_1\), pero ocupando un volumen\(n_1{\overline{V}}_1\). En el lado aguas abajo, hay\(n_2+1\) moles de gas a presión\(P_2\), ocupando volumen\(\left(n_2+1\right){\overline{V}}_2\) a una temperatura\(T_2\) y con una energía por mol de\({\overline{E}}_2\). En el lado aguas arriba,\(\Delta E_1=-\overline{E}_1\) y\(w_1=-P_1\left[n_1 \overline{V}_1-\left(n_1+1\right) \overline{V}_1 \right]=P_1 \overline{V}_1\)

En el lado aguas abajo,\(\Delta E_2={\overline{E}}_2\), y

\[w_2=-P_2\left[\left(n_2+1\right){\overline{V}}_1-n_2{\overline{V}}_1\right]=-P_2{\overline{V}}_2\]

Dado que el proceso es adiabático, cualquier calor que absorba el gas aguas arriba debe ser entregado por el gas aguas abajo, de manera que\(q_1+q_2=0\). Para el proceso de mover el mol de gas a través del tapón,

\[\Delta E=\Delta E_1+\Delta E_2=-\overline{E}_1+\overline{E}_2=q_1+q_2+w_1+w_2=P_1\overline{V}_1-P_2\overline{V}_2\]

de la cual

\[{\overline{E}}_1+P_1{\overline{V}}_1={\overline{E}}_2+P_2{\overline{V}}_2\]o\[{\overline{H}}_1={\overline{H}}_2\]

para que tengamos\(\Delta H=0\) para la expansión.

En la práctica, es conveniente medir presiones y temperaturas aguas abajo,\(P_2\) y\(T_2\), en una serie de experimentos en los que la presión y temperatura aguas arriba,\(P_1\) y\(T_1\), son constantes. La entalpía del gas es la misma en cada uno de estos puntos de presión-temperatura. Una gráfica de estos puntos es una curva isentálpica (entalpía constante). A cualquier presión y temperatura dadas, el coeficiente de Joule-Thomson,\({\mu }_{JT}\), es la pendiente de esta curva.

También podemos expresar\(\mathrm{\ }{\mu }_{JT}\) en función de la capacidad calorífica,\(C_P\), y el coeficiente de expansión térmica,\(\alpha\), donde\(\alpha =V^{-1}{\left({\partial V}/{\partial T}\right)}_P\). Comenzamos\(d\overline{H}\) expresando en función de la temperatura y la presión:

\[d\overline{H}={\left(\frac{\partial \overline{H}}{\partial T}\right)}_PdT+{\left(\frac{\partial \overline{H}}{\partial P}\right)}_TdP\]

Si dividimos\(dP\) y mantenemos\(\overline{H}\) constantes, obtenemos

\[0={\left(\frac{\partial \overline{H}}{\partial T}\right)}_P{\left(\frac{\partial T}{\partial P}\right)}_{\overline{H}}+{\left(\frac{\partial \overline{H}}{\partial P}\right)}_T\]

para que

\[{\mu }_{JT}={\left(\frac{\partial T}{\partial P}\right)}_{\overline{H}}=-{{\left(\frac{\partial \overline{H}}{\partial P}\right)}_T}/{{\left(\frac{\partial \overline{H}}{\partial T}\right)}_P}=-\frac{1}{C_P}{\left(\frac{\partial \overline{H}}{\partial P}\right)}_T\]

Si sustituimos el coeficiente de expansión térmica en la expresión por lo\({\left({\partial \overline{H}}/{\partial P}\right)}_T\) que desarrollamos en la Sección 10.5, tenemos

\[{\left(\frac{\partial \overline{H}}{\partial P}\right)}_T=\overline{V}-T{\left(\frac{\partial \overline{V}}{\partial T}\right)}_P=\overline{V}-\alpha \overline{V}T=\overline{V}\left(1-\alpha T\right)\]

Para un gas ideal,\({\left({\partial \overline{V}}/{\partial T}\right)}_P={\overline{V}}/{T}\), para que ambos\({\left({\partial \overline{H}}/{\partial P}\right)}_T\) y\({\mu }_{JT}\) sean cero. Por gases reales, sustituimos en la expresión\({\mu }_{JT}\) para encontrar

\[{\mu }_{JT}={\left(\frac{\partial T}{\partial P}\right)}_{\overline{H}}=-\frac{1}{C_P}{\left(\frac{\partial \overline{H}}{\partial P}\right)}_T=-\frac{\overline{V}}{C_P}\left(1-\alpha T\right)\]

Dado\(\overline{V}\) y cualesquiera dos de\({\mu }_{JT}\),\(C_P\), o\(\alpha\), podemos encontrar el tercero a partir de esta relación.

Haciendo las mismas sustituciones usando los derivados parciales que encontramos anteriormente para un gas van der Waals, encontramos

\[{\mu }_{JT}=-\frac{1}{C_P}\left(\overline{V}-\frac{RT}{\gamma \left(P,\overline{V}\right)}\right)\]

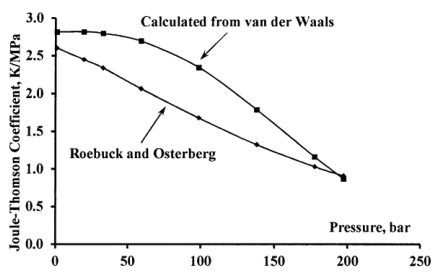
Dado que la ecuación de van der Waals simplifica demasiado los efectos de las fuerzas intermoleculares, podemos anticipar que es probable que el cálculo del coeficiente de Joule-Thomson a partir de los parámetros de van der Waals sea cualitativamente correcto, pero en escasa concordancia cuantitativa con los resultados experimentales. La Figura 4 compara las curvas calculadas y experimentales para el coeficiente de Joule-Thomson de gas nitrógeno a 0 C de 1 a 200 bar. (Los valores calculados toman\(a=0.137\mathrm{\ Pa}\ {\mathrm{m}}^{\mathrm{6}}\mathrm{\ }{\mathrm{mol}}^{--\mathrm{2}}\) y\(b=3.81\times {10}^{-5}\ {\mathrm{m}}^{\mathrm{3}}\mathrm{\ }{\mathrm{mol}}^{--\mathrm{1}}\). Los datos experimentales son de la referencia 1.)

Figura 4. El coeficiente de Joule-Thomson para\(N_2\) a 0 C

Anticipamos que el coeficiente de Joule-Thomson se convierte en cero a presiones y temperaturas donde los efectos de las atracciones intermoleculares y las repulsiones se compensan exactamente entre sí. Para las interacciones entre moléculas, las fuerzas atractivas tienen el efecto dominante a largas distancias, mientras que las fuerzas repulsivas dominan a distancias cortas. Cuanto menor sea la presión, mayor será la distancia promedio entre las moléculas de gas. Por lo tanto, a cualquier temperatura dada y a una presión suficientemente baja, los efectos de las fuerzas de atracción intermoleculares son más importantes que los de las fuerzas repulsivas intermoleculares. A presiones bajas, el coeficiente de Joule-Thomson debe ser positivo. A medida que aumenta la presión, los efectos de las fuerzas tanto atractivas como repulsivas deben aumentar, pero a una presión suficientemente alta, la distancia intermolecular promedio se vuelve tan pequeña que los efectos de las fuerzas repulsivas intermoleculares se vuelven dominantes. Por lo tanto, anticipamos que el coeficiente de Joule-Thomson disminuye a medida que aumenta la presión, llegando a ser negativo.

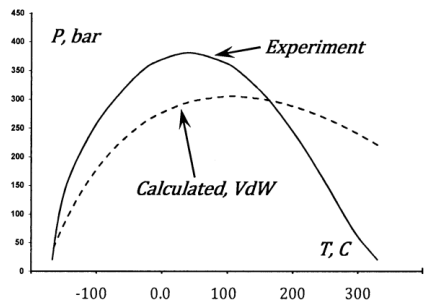
Los experimentos confirman estas expectativas. Una temperatura y presión a la que el coeficiente de Joule-Thomson se convierte en cero se denomina punto de inversión de Joule-Thomson. La curva experimentalmente determinada para el gas nitrógeno \({}^{1}\)se grafica en la Figura 5. El modelo de van der Waals también exhibe este efecto. La curva de inversión se puede encontrar a partir de la expresión\({\mu }_{JT}\) desarrollada anteriormente para un gas van der Waals. La curva de inversión para nitrógeno que se encuentra de esta manera también se grafica en la Figura 5. Cualitativamente, el acuerdo es una confirmación satisfactoria de la interpretación básica que hemos dado para el papel de las fuerzas intermoleculares. Cuantitativamente, el acuerdo es pobre, como esperamos dado el carácter excesivamente sencillo del modelo de van der Waals.

Figura 5. La temperatura de inversión de Joule-Thomson para\(N_2\) (ver referencia 1)

El coeficiente de Joule-Thomson para un gas ideal es cero, y normalmente esperamos que las propiedades de los gases reales se acerquen a las de un gas ideal ya que la presión cae a cero. Sin embargo, tanto el experimento como el modelo de van der Waals indican que el coeficiente de Joule-Thomson converge a un valor finito a medida que la presión disminuye a cero a una temperatura fija. Un modelo termodinámico estadístico \({}^{2}\)también predice este resultado. Este modelo calcula los coeficientes en la ecuación virial de estado. En ella, el segundo coeficiente virial refleja el efecto neto de fuerzas atractivas y repulsivas entre un par de moléculas, y es el segundo coeficiente virial y su derivada de temperatura determinan que el valor de\({\left({\partial \overline{H}}/{\partial P}\right)}_T\). (Los coeficientes viriales de orden superior reflejan interacciones entre un mayor número de moléculas).