12.5: Otra perspectiva sobre el principio de Le Chatelier

Cuando aplicamos el principio de Le Chatelier, imaginamos un sistema de equilibrio sobre el que imponemos algún cambio paso a paso. Inmediatamente después de la imposición de este cambio, aislamos el sistema de todas las interacciones posteriores con su entorno. Este sistema aislado es un constructo hipotético, que sólo puede aproximarse en cualquier experimento real. Tiene características peculiares: Si bien el sistema cambiado y aislado tiene las propiedades del sistema original, también es libre de sufrir un cambio adicional que el sistema original no pudo. El hipotético sistema aislado ya no está en equilibrio; puede sufrir un proceso espontáneo de cambio adicional hasta alcanzar una nueva posición de equilibrio. El principio afirma que este cambio ulterior se opone al cambio impuesto.

El principio es inherentemente cualitativo. Esto contribuye a su utilidad en el sentido de que no tenemos que contar con datos cuantitativos para poder utilizarlos. Sin embargo, una predicción cualitativa es menos útil que una cuantitativa. Intentemos ahora aplicar nuestros modelos cuantitativos basados en la segunda ley a la secuencia de cambios previstos por el principio de Le Chatelier. Comenzamos por reafirmar el principio en un lenguaje más matemático. A continuación, se ilustran estas ideas para el caso específico del equilibrio vapor-líquido con la temperatura y la presión como variables independientes.

Supongamos que\(W\)\(X\),\(Y\), y\(Z\) son un conjunto de variables termodinámicas que son adecuadas para especificar el estado del sistema. En cualquier estado de equilibrio, la entropía del sistema es entonces una función de estas variables; tenemos\(S=S\left(W,X,Y,Z\right)\). Para los propósitos actuales, asumimos que conocemos la función\(S\left(W,X,Y,Z\right)\). Dados pequeños cambios\(dW\),\(dX\),\(dY\),\(dZ\), y, en las variables independientes, podemos encontrar el cambio en\(dS\) para una transición reversible de\(\left(W,X,Y,Z\right)\) a\(\left(W+dW,X+dX,Y+dY,Z+dZ\right)\):

\[dS={\left(\frac{\partial S}{\partial W}\right)}_{XYZ}dW+{\left(\frac{\partial S}{\partial X}\right)}_{WYZ}dX+{\left(\frac{\partial S}{\partial Y}\right)}_{WXZ}dY+{\left(\frac{\partial S}{\partial Z}\right)}_{WXY}dZ\]

Cuando imponemos el cambio creando el hipotético sistema aislado, imaginamos que alguna característica del sistema cambia instantáneamente, y que lo hace sin cambiar las otras propiedades del sistema. Dado que suponemos que nada del sistema cambia en el paso de perturbación y aislamiento, la entropía del sistema perturbado, aislado, hipotético sigue siendo la misma que la del sistema de equilibrio original.

Figura 2. Procesos espontáneos y reversibles que conectan los mismos estados de equilibrio.

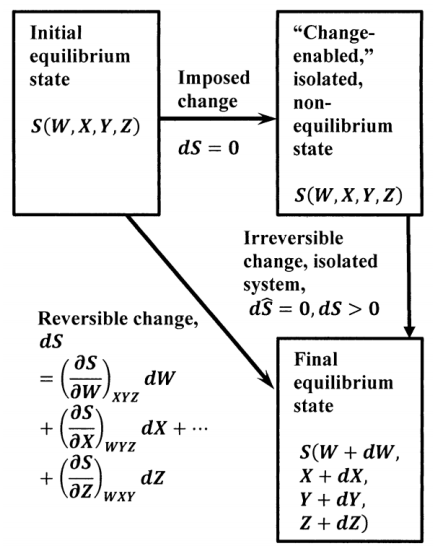
La Figura 2 muestra las entropías para tres estados en el ciclo que comprende el modelo de Le Chatelier para el cambio. La entropía del sistema de equilibrio original es\(S\left(W,X,Y,Z\right)\) y la del sistema de equilibrio final es\(S\left(W+dW,X+dX,Y+dY,Z+dZ\right)\). El mismo estado de equilibrio final se alcanza tanto por la transición irreversible desde el estado hipotético habilitado para el cambio como por una transición reversible desde el estado de equilibrio inicial. Dado que la entropía es una función de estado, su cambio alrededor de este ciclo debe ser cero. De ahí que los cambios incrementales\(dW\)\(dX\)\(dY\),,, y\(dZ\) que ocurren en las variables termodinámicas deben satisfacer la desigualdad

\[{\left(\frac{\partial S}{\partial W}\right)}_{XYZ}dW+{\left(\frac{\partial S}{\partial X}\right)}_{WYZ}dX+{\left(\frac{\partial S}{\partial Y}\right)}_{WXZ}dY +{\left(\frac{\partial S}{\partial Z}\right)}_{WXY}dZ>0\]

Podemos ver la aplicación de esta desigualdad al sistema hipotético, habilitado para el cambio y aislado como una expresión matemática del principio de Le Chatelier. Para ver esto más claramente, supongamos que somos capaces de mantenernos\(W\) y\(Z\) constantes. Suponemos que el cambio impuesto requiere que el valor final de\(X\) ser\(X+dX\). Para que el sistema se mantenga en equilibrio, la variable restante,\(Y\), debe cambiar en una cantidad,\(dY\), que satisfaga esta desigualdad. Es decir, para alcanzar el nuevo estado de equilibrio, el cambio en\(Y\) debe satisfacer

\[{\left(\frac{\partial S}{\partial X}\right)}_{WYZ}dX+{\left(\frac{\partial S}{\partial Y}\right)}_{WXZ}dY>0\]

En este modelo, las variables\(X\) y\(Y\) impulsan la entropía cambian a medida que el sistema hipotético se mueve hacia su nueva posición de equilibrio. El cambio impuesto en\(X\) los cambios la entropía del sistema por

\[dS_{imposed}={\left(\frac{\partial S}{\partial X}\right)}_{WYZ}dX\]

Dado que el efecto del cambio impuesto es alejar al sistema de su posición de equilibrio original, tenemos\(dS_{imposed}<0\). La respuesta del sistema cambia la entropía del sistema al

\[dS_{response}={\left(\frac{\partial S}{\partial Y}\right)}_{WXZ}dY\]

Tenemos\(dS_{response}>-dS_{imposed}>0\), para que podamos describir razonablemente la respuesta,\(dY\), que hace\(dS_{response}>0\), como un cambio que se opone al cambio impuesto,\(dX\), que hace\(dS_{imposed}<0\).

Aplicar el principio de Le Chatelier es una especie de arte. Un elemento central de este arte es la capacidad de idear un estado hipotético, habilitado para el cambio, aislado y de no equilibrio que sea un buen modelo para el estado inicial del proceso espontáneo. En la Sección 6.6, utilizamos argumentos cualitativos para aplicar el principio de Le Chatelier al equilibrio vapor-líquido. Para relacionar estos argumentos cualitativos con el modelo matemático que hemos desarrollado, consideremos el experimento gedanken representado en la Figura 3. Suponemos que el sistema de equilibrio inicial contiene el líquido y vapor de una sustancia pura a presión,\(P\), y temperatura,\(T\). Imaginamos que podemos crear el hipotético sistema aislado imponiendo un cambio escalonado a la presión aplicada sin cambiar la presión del sistema.

Figura 3. Procesos espontáneos y reversibles que conectan los mismos estados de equilibrio líquido-vapor.

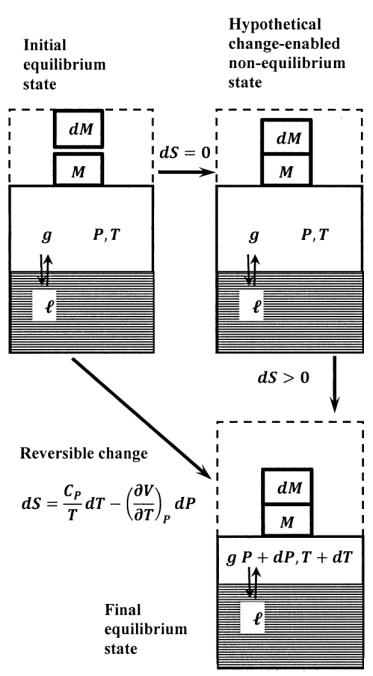
Para modelar la perturbación de presión, veamos la mezcla líquido-vapor como un subsistema, que está encerrado en un cilindro vertical sellado por un pistón sin fricción. Una masa,\(M\), descansa sobre la parte superior del pistón. Para los propósitos actuales, consideramos que esta masa es una porción de un segundo subsistema. La fuerza gravitacional sobre esta masa crea la presión aplicada a la mezcla líquido-vapor. Dado que este es un estado de equilibrio de la sustancia, esta presión aplicada es igual a la presión\(P\),, del subsistema líquido-vapor. Una pequeña masa\(dM\),, también forma parte del segundo subsistema. En este estado de equilibrio original del sistema, esta masa menor se soporta de alguna manera, de manera que no contribuye a la presión aplicada. Suponemos que el pistón es un aislante térmico perfecto, por lo que no se puede intercambiar calor entre los dos subsistemas.

Como se esboza en la Figura 3, creamos el sistema hipotético habilitado para el cambio moviendo la masa más pequeña para que también descanse sobre la parte superior del pistón. Inmediatamente después, aislamos completamente el sistema del resto del universo. Suponemos que la presión aplicada aumenta instantáneamente a\(P+dP\). Sin embargo, dado que el subsistema líquido-vapor no ha cambiado, suponemos que la presión, la entropía y todas las demás propiedades termodinámicas del subsistema líquido-vapor permanecen sin cambios en este estado hipotético. El sistema no está en equilibrio en este hipotético estado, porque la presión aplicada no es igual a la del subsistema líquido-vapor. Se puede producir un cambio espontáneo a un nuevo estado de equilibrio. Debido a que el sistema está aislado,\(\Delta \hat{S}=0\). Por lo tanto, tenemos\(\Delta S>0\). La temperatura de equilibrio final es\(T+dT\).

Con la presión y la temperatura como variables independientes, este modelo para el principio de Le Chatelier da lugar al siguiente requisito matemático:

\[dS=T^{-1}{\left({\partial H}/{\partial T}\right)}_PdT-{\left({\partial V}/{\partial T}\right)}_PdP>0.\]

Eso lo sabemos\(T\),\({\left({\partial H}/{\partial T}\right)}_P\), y\({\left({\partial V}/{\partial T}\right)}_P\) son positivos. Por lo tanto podemos reorganizar la desigualdad para encontrar

\[dT>T\left[{{\left(\frac{\partial V}{\partial T}\right)}_P}/{{\left(\frac{\partial H}{\partial T}\right)}_P}\right]dP\]

Si tenemos\(dP>0\), se deduce que\(dT>0\); es decir, la temperatura de equilibrio líquido-vapor aumenta con la presión.