12.6: Equilibrios de fase - Dependencia de temperatura del punto de ebullición

En las Secciones 12.4 y 12.6, exploramos dos enfoques para utilizar el criterio basado en la entropía para el cambio espontáneo. Al discutir el derretimiento del hielo en\(\mathrm{+10}\) C, calculamos los cambios de entropía tanto para el sistema como para el entorno para demostrarlo\(\Delta S_{universe}>0\), como lo requiere la segunda ley para un proceso espontáneo. Al discutir la dependencia de la presión del punto de ebullición de un líquido en la Sección 12.6, relacionamos el criterio de la segunda ley para el cambio espontáneo con el principio de Le Chatelier. Pasamos ahora a especificar las presiones y temperaturas a las que se encuentran en equilibrio dos fases de una sustancia pura. Cuando elegimos presión y temperatura como variables independientes, los criterios de energía libre de Gibbs especifican el estado de equilibrio y la dirección del cambio espontáneo.

Para un proceso reversible en el que todo el trabajo es trabajo de presión-volumen y en el que la presión y la temperatura cambian por\(dP\) y\(dT\), el cambio en la energía libre de Gibbs es\(dG=VdP-SdT\). Apliquemos esta relación al problema de equilibrio líquido-vapor que discutimos en la Sección 12.6. Para ello, vemos el proceso desde una perspectiva ligeramente diferente. Suponemos que tenemos dos sistemas. Estos son idénticos a los estados inicial y final del sistema en nuestra discusión anterior. Uno de estos sistemas está en equilibrio líquido-vapor a una presión y temperatura particulares\(\ T\).\(P\) El otro está en equilibrio líquido-vapor en\(P+dP\) y\(T+dT\). Consideramos el cambio en la energía libre de Gibbs de un mol de la sustancia a medida que atraviesa reversiblemente el ciclo esbozado en la Figura 4.

Figura 4. Diferencias molares de energía libre de Gibbs entre dos estados de equilibrio líquido-vapor.

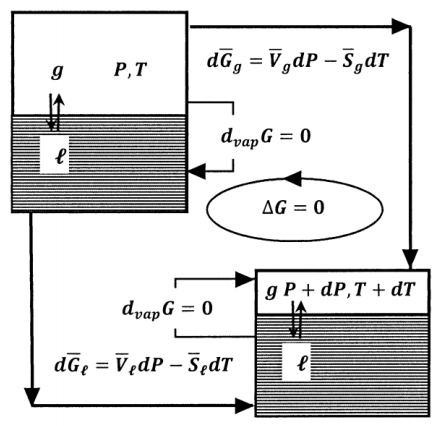
La presión y la temperatura son constantes en cada uno de los dos estados de equilibrio. En cualquiera de estos estados de equilibrio, la energía libre de Gibbs no cambia cuando un mol de líquido se convierte en su gas,\({\Delta }_{vap}G\left(P,T\right)=0\) y\({\Delta }_{vap}G\left(P+dP,T+dP\right)=0\). Cuando la presión y la temperatura de un mol de líquido cambian de\(P\) y\(T\) hacia\(P+dP\) y\(T+dT\), el cambio de energía libre de Gibbs es\(d\overline{G}\left(\ell \right)=\overline{V}_{\ell }dP- \overline{S}_{\ell }dT\). Por un mol de gas, este cambio en la presión y la temperatura cambian la energía libre de Gibbs por\(d\overline{G}\left(g\right)= \overline{V}_gdP- \overline{S}_gdT\). (\(\overline{V}_{\ell }\),\(\overline{V}_g\),\(\overline{S}_{\ell }\), y\(\overline{S}_g\) se evalúan en\(P\) y\(T\). Sin embargo, dado que\(dP\) y\(dT\) son pequeñas, estas cantidades son esencialmente constantes en los rangos de presión y temperatura involucrados). Para los pasos individuales de este ciclo, tenemos

\[\left(\ell ,\ P,\ T\right)\to \left(\ell ,\ P+dP,\ T+dT\right) d\overline{G}\left(\ell \right)=\overline{V}_{\ell }dP- \overline{S}_{\ell }dT\]

\[\left(\ell ,\ P+dP,\ T+dT\right)\to \left(g,\ P+dP,\ T+dT\right) {\Delta }_{vap}G\left(P+dP,T+dT\right)=0\]

\[\left(g,\ P+dP,\ T+dT\right)\to \left(g,\ P,\ T\right) -d\overline{G}\left(g\right)=-\left(\overline{V}_gdP- \overline{S}_gdT\right)\]

\[\left(g,\ P,\ T\right)\to \left(\ell ,\ P,\ T\right) -{\Delta }_{vap}G\left(P,T\right)=0\]

Dado que la energía libre de Gibbs es una función de estado, la suma de estos términos es cero. Tenemos

\[{\Delta }_{vap}G\left(P+dP,T+dT\right)-{\Delta }_{vap}G\left(P,T\right) +d\overline{G}\left(\ell \right)-d\overline{G}\left(g\right) =d\overline{G}\left(\ell \right) -d\overline{G}\left(g\right) =0\]

así que eso\(d\overline{G}\left(\ell \right)=d\overline{G}\left(g\right)\). Es decir, la energía libre de Gibbs del líquido cambia en la misma cantidad que la energía libre de Gibbs del gas cuando se toma un mol de cualquiera de los dos de un estado de equilibrio líquido-vapor a otro. Sustituyendo, encontramos una condición que los cambios de presión y temperatura deben satisfacer cuando el sistema pasa del estado de equilibrio líquido-vapor\(\left(P,T\right)\) al estado de equilibrio líquido-vapor en\(\left(P+dP,T+dT\right)\):

\[\left( \overline{V}_g- \overline{V}_{\ell }\right)dP-\left(\overline{S}_g-\overline{S}_{\ell }\right)dT=0\]

Dejamos\({\Delta }_{vap}\overline{V}= \overline{V}_g- \overline{V}_{\ell }\) y\({\Delta }_{vap}\overline{S}=\overline{S}_g-\overline{S}_{\ell }\), dónde\({\Delta }_{vap}\overline{V}\) y\({\Delta }_{vap}\overline{S}\) son los cambios de volumen y entropía que acompañan a la vaporización de un mol del líquido a\(P\) y\(T\). \({\Delta }_{vap}\overline{V}\)y\({\Delta }_{vap}\overline{S}\) son esencialmente constantes en los pequeños rangos de presión y temperatura involucrados. Sustituyendo, tenemos\({\Delta }_{vap}\overline{V}dP-{\Delta }_{vap}\overline{S}dT=0\), que podemos reorganizar para dar

\[\frac{dP}{dT}=\frac{\Delta _{vap}\overline{S}}{\Delta _{vap}\overline{V}}\]

A medida que un mol de líquido se vaporiza reversiblemente en\(P\) y\(T\), el sistema acepta calor\(q^{rev}_P=\Delta _{vap}\overline{H}\). Por lo tanto, la entropía de vaporización en\(P\) y\(T\) es\({\Delta }_{vap}\overline{S}={\Delta }_{vap}\overline{H}/T\), y la relación entre\(dP\) y\(dT\) se convierte

\[\frac{dP}{dT}=\frac{\Delta _{vap}\overline{H}}{T \Delta _{vap}\overline{V}}\]

A continuación vemos que tal relación se mantiene para cualquier equilibrio entre dos fases puras. La relación general se llama la ecuación de Clapeyron.

Este análisis es exitoso porque los constituyentes son fases puras; las propiedades del líquido son independientes de la cantidad de vapor presente y viceversa. Cuando analizamos el equilibrio entre una solución líquida y un gas de los componentes de la solución, el problema es más complejo, porque las propiedades de las fases dependen de sus composiciones.