12.7: Equilibrios de fase - Dependencia de temperatura del punto de fusión

También podemos representar cambios reversibles por rutas en mapas de contorno. En la Figura 5, una superficie de energía libre de Gibbs se representa como un mapa de contorno.

Figura 5. El camino de un sistema cambiante representado en un mapa de contornos constantes de energía libre de Gibbs.

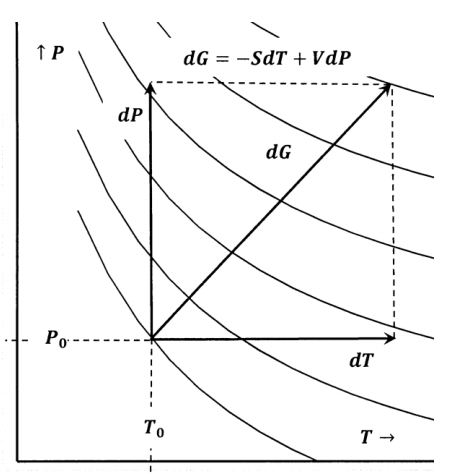
Para pequeños cambios en\(T\) y\(P\), podemos evaluar

\[dG=G\left(P_0+dP,T_0+dT\right)-G\left(P_0,T_0\right)\]

de

\[dG=-S\left(P_0,T_0\right)dT+V\left(P_0,T_0\right)dP\]

Para cambios más grandes, podemos integrarnos a lo largo de los caminos\(P=P_0\) y\(T=T_0+\Delta T\) encontrar

\[\Delta G=\int^{T_0+\Delta T}_{T_0}{-S\left(P_0,T\right)dT+}\int^{P_0+\Delta P}_{P_0}{V\left(P,T_0+\Delta T\right)dP}\]

El cálculo de\(\Delta S\) la Sección 12.5 podría representarse de manera similar como una trayectoria en el plano de temperatura-presión que conecta dos contornos de entropía constante.

El análisis del equilibrio sólido-líquido es paralelo al del equilibrio líquido-vapor. Consideremos nuevamente el equilibrio entre el hielo y el agua. Dado que el hielo y el agua están en equilibrio a una temperatura y presión particulares, y suponiendo que aumentemos la presión a partir de este valor de equilibrio, ¿cómo debe cambiar la temperatura para que el sistema permanezca en equilibrio? En la Sección 6.6, utilizamos el principio de Le Chatelier para responder cualitativamente a esta pregunta. Ahora, encontramos una respuesta cuantitativa por un argumento que es muy paralelo al de la Sección 12.7.

Figura 6. Cambios energéticos libres de Gibbs en un ciclo que conecta dos estados de equilibrio sólido-líquido.

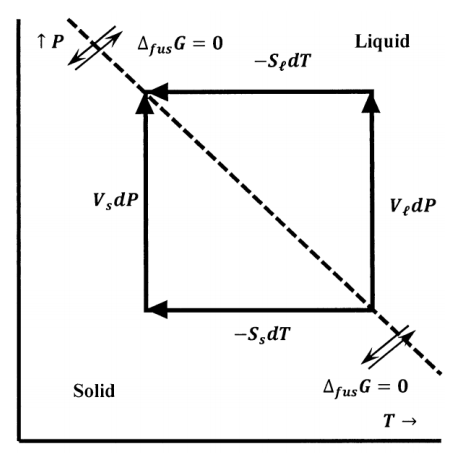
La Figura 6 representa la línea de presiones y temperaturas a lo largo de la cual el hielo y el agua están en equilibrio. Podemos ver esto como un mapa de contorno. En este caso, los contornos son conjuntos de presiones y temperaturas para las cuales\({\Delta }_{fus}\overline{G}\) es constante. Solo se muestra el contorno para\({\Delta }_{fus}\overline{G}=0\). La figura también representa caminos a lo largo de los cuales el hielo y el agua se pueden tomar individualmente desde su estado de equilibrio en\(P\) y\(T\) hasta su estado de equilibrio en\(P+dP\) y\(T+dT\). El cambio de energía libre de Gibbs para el hielo debe ser igual al del agua. Dejando\({\overline{G}}_{\ell }\)\({\overline{S}}_{\ell }\), y\({\overline{V}}_{\ell }\) ser la energía libre de Gibbs, la entropía, y el volumen de un mol de agua a temperatura\(T\) y presión\(P\), la ecuación

\[d{\overline{G}}_{\ell }={\overline{V}}_{\ell }dP-{\overline{S}}_{\ell }dT\]

especifica el cambio en la energía libre de Gibbs de un mol de agua cuando la presión cambia\(P\) a\(P+dP\) y la temperatura cambia de\(T\) a\(T+dT\). Del mismo modo, usando el subíndice “s” para denotar hielo, tenemos

\[d{\overline{G}}_s={\overline{V}}_sdP-{\overline{S}}_sdT\]

Dado que estos cambios de energía libre de Gibbs conectan estados de equilibrio hielo-agua, deben ser iguales, y tenemos

\[d{\overline{G}}_{\ell }-d{\overline{G}}_s=\left({\overline{V}}_{\ell }-{\overline{V}}_s\right)dP-\left({\overline{S}}_{\ell }-{\overline{S}}_s\right)dT={\Delta }_{fus}\overline{V}dP-{\Delta }_{fus}\overline{S}dT=0\]

donde introducimos\({\Delta }_{fus}\overline{S}\) y\({\Delta }_{fus}\overline{V}\) para representar la entropía y los cambios de volumen que ocurren cuando un mol de hielo se funde reversiblemente en\(P\) y\(T\). Reorganizar da

\[\frac{dP}{dT}=\frac{\Delta_{fus}\overline{S}}{\Delta_{fus}\overline{V}}\]

Desde

\[\Delta_{fus}\overline{S}={\Delta_{fus}\overline{H}}/{T},\]

la ecuación de Clapeyron se convierte en

\[\frac{dP}{dT}=\frac{\Delta_{fus}\overline{H}}{T\ {\Delta }_{fus}\overline{V}}\]

A una presión de una barra y una temperatura de 273.15 K, la entalpía de fusión es\(\mathrm{6010}\ \mathrm{J}\ {\mathrm{mol}}^{\mathrm{-1}}\ {\mathrm{K}}^{-1}\). El valor de entalpía cambia solo lentamente a medida que cambia la temperatura de equilibrio. Los volúmenes de un mol de hielo y un mol de agua son 19.651 y 18.019\({\mathrm{cm}}^3\), respectivamente. A 273.15 K, obtenemos

\[\frac{dP}{dT}=-143.7\ \mathrm{bar}\ {\mathrm{K}}^{-1}\]

Si la presión aumenta a 1000 bar, el cambio en el punto de fusión es de aproximadamente —6.96 K, así que eso\(T_{mp}\left(1000\ \mathrm{bar}\right)=266.2\ \mathrm{K}\).

Nuevamente, este análisis es exitoso porque los constituyentes son fases puras; las propiedades del hielo son independientes de la cantidad de agua presente y viceversa. Cuando analizamos el equilibrio entre el hielo y el agua salada, las propiedades del agua salada dependen del tipo de sal presente y de su concentración.