13.6: El Cambio y Equilibrio Estándar de Energía Libre de Gibbs en Reacciones de Gases Ideales

Última actualización
Guardar como PDF

Page ID: 73961

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

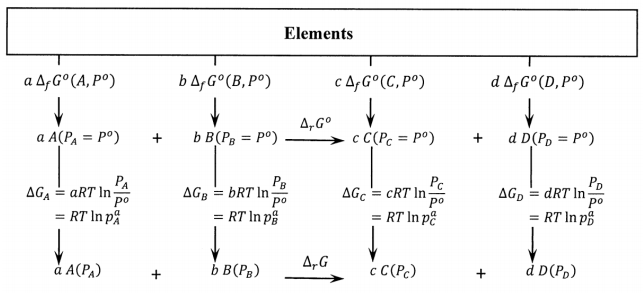
Screen Shot 2019-10-11 a las 9.52.25 AM.png — Figura 5. Ciclo demostrando la relación entre\(\Delta_r G\) y\(\Delta_r G^o\).

La relación entre\({\Delta }_rG\) y\({\Delta }_rG^o\) es evidente a partir del ciclo en la Figura 5. Ya que hemos demostrado que\({\Delta }_{sep}G\left(P_A,P_B,P_C,P_D\right)={\Delta }_rG\left(P_A,P_B,P_C,P_D\right)\), podemos considerar la ecuación inferior en este ciclo para representar la reacción que ocurre en una mezcla mientras se calcula su cambio de energía libre como la diferencia de energía libre entre productos puros y reactivos puros. Dado que\({\Delta }_{cycle}G=0\),

\[{\Delta }_{cycle}G={\Delta }_rG^o-{\Delta }_rG+RT\left({ \ln p^c_C\ }+{ \ln p^d_D\ }-{ \ln p^a_A\ }-{ \ln p^B_B\ }\right)=0\]

que se puede reorganizar al resultado obtenido en el § 2:

\[{\Delta }_rG={\Delta }_rG^o+RT{ \ln \frac{p^c_Cp^d_D}{p^a_Ap^b_B}\ }\]

\({\Delta }_rG\)es el cambio de energía libre de Gibbs para una unidad de la reacción que ocurre en un sistema cuya composición se especifica por\(P_A\),\(P_B\),\(P_C\), y\(P_D\). En este sistema de reacción espontánea, la energía molar libre de Gibbs del gas ideal\(A\) es

\[{\overline{G}}_A\left(P_A\right)={\Delta }_fG^o\left(A,P^o\right)+RT{ \ln p_A\ }\]

Si el sistema está en equilibrio,\(P_A\),\(P_B\)\(P_C\), y\(P_D\) son presiones de equilibrio; estos valores caracterizan un estado de equilibrio. Entonces\({\Delta }_rG\) es el cambio de energía libre para una reacción que ocurre en equilibrio a presión y temperatura constantes, y\({\Delta }_rG\) es cero. La ecuación

\[0={\Delta }_rG^o+RT{ \ln \frac{p^c_Cp^d_D}{p^a_Ap^b_B}\ }\]

es exacto. Tenemos, cuando las presiones parciales son las de un sistema en equilibrio,

\[{\Delta }_rG^o=-RT{ \ln \frac{p^c_Cp^d_D}{p^a_Ap^b_B}\ }\]

Dado que\({\Delta }_rG^o\) es una constante, se deduce que

\[\frac{p^c_Cp^d_D}{p^a_Ap^b_B}\]

es una constante. Es, por supuesto, la constante de equilibrio. Tenemos

\[K_P=\frac{p^c_Cp^d_D}{p^a_Ap^b_B}\]

y\[{\Delta }_rG^o=-RT{ \ln K_P\ }\]

o, resolviendo\(K_P\)

\[K_P = \mathrm{exp}\left( + \frac{{\mathrm{\Delta }}_rG^o}{RT}\right)\]

Tenga en cuenta que el valor de la constante de equilibrio se calcula a partir del cambio de energía libre de Gibbs en condiciones estándar, no del cambio de energía libre de Gibbs en equilibrio, que es cero.