14.11: Volver a la Fugacidad- la Fugacidad de Un Componente de Una Mezcla de Gases

En el Capítulo 11, introducimos la fugacidad como medida alternativa de la diferencia entre la energía libre de Gibbs de un mol de un gas puro en su hipotético estado estándar de gas ideal y su energía libre de Gibbs en cualquier otro estado a la misma temperatura. Esta definición hace que la fugacidad de un gas sea una función intensiva de presión y temperatura. A una temperatura fija, el estado de un mol de un gas puro se especifica por su presión, y la fugacidad es función únicamente de la presión. La fugacidad tiene las unidades de presión. Dando efecto a nuestra decisión de dejar que la fugacidad del gas sea unidad cuando el gas se encuentre en su hipotético estado estándar de gas ideal\(({HIG}^o)\) y utilizando la energía de formación libre de Gibbs para el gas en este estado como la energía libre estándar de Gibbs para la fugacidad, definimos la fugacidad de un gas puro\(A\), por la ecuación

\[{\overline{G}}_A\left(P\right)={\Delta }_fG^o\left(A,{HIG}^o\right)+RT{ \ln \left[\frac{f_A\left(P\right)}{f_A\left({HIG}^o\right)}\right]\ }\]

Para sustancia\(A\) en cualquier sistema, el potencial químico es la energía parcial libre molar; es decir,\({\mu }_A\left(P,T\right)={\overline{G}}_A\left(P,T\right)\). Dado que la energía libre de Gibbs de formación se define para un mol de sustancia pura a una presión y temperatura especificadas, es una cantidad molar parcial. Cuando elegimos utilizar el hipotético gas ideal a una presión de una barra como estado estándar para la energía libre de Gibbs de formación del gas, también establecemos la energía libre de Gibbs de formación del gas ideal hipotético en su estado estándar como el potencial químico de estado estándar; es decir,\({\mu }^o_A={\Delta }_fG^o\left(A,{HIG}^o\right)\). De ahí que también podamos expresar la fugacidad de un gas mediante la ecuación

\[{\mu }_A\left(P\right)={\Delta }_fG^o\left(A,{HIG}^o\right)+RT{ \ln \left[\frac{f_A\left(P\right)}{f_A\left({HIG}^o\right)}\right]\ }\]o\[{\mu }_A\left(P\right)={\mu }^o_A+RT{ \ln \left[\frac{f_A\left(P\right)}{f_A\left({HIG}^o\right)}\right]\ }\] (gas real puro)

Para una mezcla de gases reales, podemos extender la definición de fugacidad de manera natural. Queremos que la fugacidad de un gas componente mida la diferencia entre su potencial químico en la mezcla\(\mu\), y su potencial químico en su estado estándar\({\mu }^o\), donde su estado estándar es el gas ideal hipotético puro a una barra de presión. Si el gas\(A\) es un componente de un sistema de gas mixto a temperatura constante, tenemos\({d\mu }_A={\overline{V}}_AdP\), donde\({\overline{V}}_A\) está el volumen molar parcial de\(A\) en el sistema, y\(P\) es la presión del sistema. Encontremos\({\mu }_A\) en una mezcla binaria que contenga un mol de\(A\) y\(n_B\) moles de un segundo componente,\(B\). Dejar que el volumen molar parcial de\(B\) ser\({\overline{V}}_B\). El volumen del sistema es\(V={\overline{V}}_A+n_B{\overline{V}}_B\). Las fracciones molares de\(A\) y\(B\) son\(x_A={1}/{\left(n_B+1\right)}\) y\(x_B={n_B}/{\left(n_B+1\right)}\).

Figura 1. Encontrar la energía libre de Gibbs de un gas real en una mezcla.

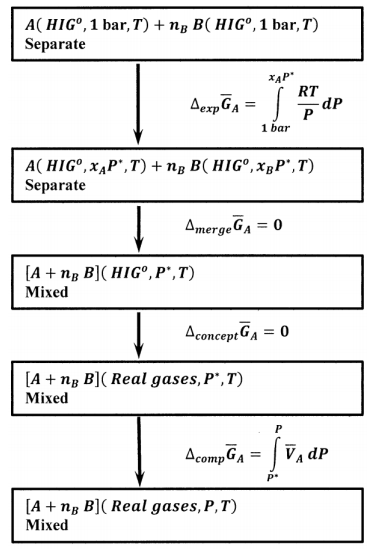
Para encontrar el cambio en\({\mu }_A\), necesitamos un proceso reversible que lleve un mol de\(A\) en su estado estándar a una mezcla de un mol\(A\) con\(n_B\) moles de\(B\), en el que se encuentre la presión de la mezcla\(P\). El proceso de cuatro etapas descrito en la Figura 1 responde a nuestros requisitos: Un mol de\(A\) y\(n_B\) moles de\(B\) se expanden por separado de sus hipotéticos estados estándar de gas ideal, a\(P^o\), a las bajas presiones arbitrarias\(x_AP^*\) y\(x_BP^*\), respectivamente. Para esta expansión, el cambio en la energía libre de Gibbs de un mol de\(A\), que permanece en su hipotético estado gaseoso ideal, es

\[{\Delta }_{exps} \overline{G}_A=\int^{x_AP^*}_{P^o} \overline{V}^{\textrm{⦁}}_A dP= \int^{x_AP^*}_{P^o} \frac{RT}{P}dP=RT \ln \left(\frac{x_AP^*}{P^o}\right)\]

A continuación, estos gases ideales de baja presión se fusionan para formar una mezcla de un mol de\(A\) con\(n_B\) moles de\(B\) a la presión total\(P^*\). Para este proceso de fusión,\({\Delta }_{merge}{\overline{G}}_A=0\). Entonces, suponemos que los gases ideales se convierten en gases reales en una mezcla cuya presión es\(P^*\). Ya que esto es meramente un cambio conceptual, lo hemos hecho\({\Delta }_{concept}{\overline{G}}_A=0\). Finalmente, comprimimos la mezcla de gases reales de\(P^*\) a una presión arbitraria,\(\ P\). Dado que el volumen de la mezcla es\(V={\overline{V}}_A+n_B{\overline{V}}_B\), el cambio de energía libre de Gibbs para esta compresión de la mezcla es

\[{\Delta }_{comp}G_{mixture}=\int^P_{P^*}{V}dP=\int^P_{P^*}{{\overline{V}}_A}dP+n_B\int^P_{P^*}{{\overline{V}}_B}dP\]

Vemos que el cambio de energía libre de Gibbs para el sistema de gas real es la suma de los cambios de energía libre de Gibbs para los componentes; tenemos

\[{\Delta }_{comp}{\overline{G}}_A=\int^P_{P^*}{{\overline{V}}_A}dP\]

Para este proceso, tenemos

\[\begin{aligned} {\mu }_A-{\mu }^o_A & =RT \ln \left[\frac{f_A\left(P\right)}{f_A\left({HIG}^o\right)}\right] \\ ~ & ={\Delta }_{exps} \overline{G}_A+{\Delta }_{merge} \overline{G}_A+{\Delta }_{concept} \overline{G}_A+{\Delta }_{comp} \overline{G}_A \\ ~ & =RT \ln \left[\frac{x_AP^*}{P^o}\right] +\int^P_{P^*} \overline{V}_AdP-\int^P_{P^*} \frac{RT}{P}dP+\int^P_{P^*} \frac{RT}{P}dP \end{aligned}\]

donde hemos sumado y restado la cantidad

\[\int^P_{P^*}{\frac{RT}{P}}dP\]

Dividiendo por\(RT\) y evaluando la última integral, encontramos

\[ \begin{aligned} \frac{{\mu }_A-{\mu }^o_A}{RT} & = \ln \left[\frac{f_A\left(P\right)}{f_A\left({HIG}^o\right)}\right] \\ ~ & = \ln x_A\ + \ln P^*\ - \ln P^o +\int^P_{P^*} \left(\frac{\overline{V}_A}{RT}-\frac{1}{P}\right) dP+ \ln P - \ln P^* \end{aligned}\]

\(P^*\)es una presión finita arbitrariamente cercana a cero. A presiones muy bajas, el gas real\(A\) se comporta como un gas ideal; por lo tanto, a presiones muy bajas, el volumen molar parcial del gas real se aproxima bien por el volumen molar parcial del gas puro\(A\). Es decir, tenemos\({\overline{V}}_A\approx \overline{V^{\textrm{⦁}}_A}\), y

\[ \begin{aligned} \int^{P^*}_0 \left(\frac{\overline{V}_A}{RT}-\frac{1}{P}\right) dP & \approx \int^{P^*}_0 \left(\frac{\overline{V^{\textrm{⦁}}_A}}{RT}-\frac{1}{P}\right)dP \\ ~ & \approx 0 \end{aligned}\]

donde la aproximación se vuelve exacta en el límite como\(P^*\to 0\). Simplificando los términos del logaritmo natural y expandiendo la integral, obtenemos

\[ \begin{aligned} \frac{{\mu }_A-{\mu }^o_A}{RT} & = \ln \left[\frac{f_A\left(P\right)}{f_A\left({HIG}^o\right)}\right] \\ ~ & = \ln \frac{x_AP}{P^o} +\int^P_0 \left(\frac{\overline{V}_A}{RT}-\frac{1}{P}\right) dP-\int^{P^*}_0 \left(\frac{\overline{V}_A}{RT}-\frac{1}{P}\right)dP \\ ~ & = \ln \frac{x_AP}{P^o} +\int^P_0 \left(\frac{\overline{V}_A}{RT}-\frac{1}{P}\right)dP \end{aligned}\]

Definir el coeficiente de fugacidad para\(A\) en esta mezcla,\({\gamma }_A\), por\[{\gamma }_A=\frac{f_A\left(P\right)}{x_AP}\]

y recordando que\(f_A\left({HIG}^o\right)=P^o\), utilizamos este resultado para encontrar\[{ \ln {\gamma }_A\ }={ \ln \left(\frac{f_A\left(P\right)}{x_AP}\right)=\ }\int^P_0{\left(\frac{{\overline{V}}_A}{RT}-\frac{1}{P}\right)}dP\]

Esto difiere de la relación correspondiente para la fugacidad de un gas puro sólo en que el volumen molar parcial es el del gas\(A\) en una mezcla con otros gases. Esta es una diferencia trivial en principio, pero una diferencia importante en la práctica. Para encontrar la fugacidad del puro\(A\), utilizamos el volumen molar parcial del gas puro, que se calcula fácilmente a partir de cualquier ecuación empírica de estado de gas puro. Sin embargo, para obtener experimentalmente el volumen molar parcial de gas\(A\) en una mezcla de gases, debemos recolectar datos de presión-volumen-temperatura en función de la composición del sistema. Si contemplamos crear un catálogo de dichos datos para las mezclas de incluso un número modesto de compuestos, vemos que se debe recolectar una enorme cantidad de datos. Apenas el número de sistemas que involucran solo mezclas binarias es grande. Para\(N\) los compuestos, existen mezclas\(N{\left(N-1\right)}/{2}\) binarias, cada una de las cuales tendría que estudiarse en muchas composiciones para desarrollar buenos valores para los volúmenes molares parciales.

Afortunadamente, la experiencia práctica demuestra que una simple aproximación suele dar resultados satisfactorios. En esta aproximación, asumimos que el volumen molar parcial de gas\(A\) —presente en fracción molar\(x_A\) en un sistema cuya presión es\(P\) — es igual al volumen molar parcial del gas puro a la misma presión. Es decir, para una mezcla binaria de gases\(A\) y\(B\), suponemos

\[{\overline{V}}_A\left(P,x_A,x_B\right)=\overline{V^{\textrm{⦁}}_A}\left(P\right)\]

En esta aproximación, tenemos

\[\frac{{\mu }_A-{\mu }^o_A}{RT}={ \ln \frac{x_AP}{P^o}\ }+\int^P_0{\left(\frac{\overline{V^{\textrm{⦁}}_A}}{RT}-\frac{1}{P}\right)}dP\]y\[{ \ln {\gamma }_A\ }={ \ln \left(\frac{f_A\left(P\right)}{x_AP}\right)=\ }\int^P_0{\left(\frac{\overline{V^{\textrm{⦁}}_A}}{RT}-\frac{1}{P}\right)}dP\]

Hacemos la misma suposición para el gas\(B\). Del teorema de Euler sobre funciones homogéneas, tenemos\(\overline{V}=x_A{\overline{V}}_A+x_B{\overline{V}}_B\). Por lo tanto, en esta aproximación, tenemos

\[\overline{V}=x_A{\overline{V}}_A+x_B{\overline{V}}_B\approx x_A\overline{V^{\textrm{⦁}}_A}+x_B\overline{V^{\textrm{⦁}}_B}\]

La última suma es la representación legal de Amagat del volumen molar de la mezcla gaseosa. Vemos que nuestra aproximación equivale a asumir que el sistema obedece a la ley de Amagat. Físicamente, esto supone que la mezcla de gases es una solución ideal (gaseosa). Discutimos soluciones ideales en el Capítulo 16. En una solución ideal, se supone que las interacciones intermoleculares entre una\(A\)\(B\) molécula y una molécula tienen el mismo efecto que las interacciones entre dos\(A\) moléculas o entre dos\(B\) moléculas. Esto difiere de la suposición ideal-gas; no hay efecto de las interacciones entre dos moléculas de gas ideal cualquiera.