14.14: Dependencia de la Actividad de la Temperatura- Entalpías Molares Parciales Relativas

Habiendo encontrado la actividad de un componente a una temperatura, queremos poder encontrarlo a una segunda temperatura. La ecuación desarrollada en la Sección 14.13 no proporciona una manera práctica de encontrar la dependencia de la temperatura de\({\tilde{a}}_A\) o\({ \ln {\tilde{a}}_A\ }\). Podemos obtener una ecuación útil reordenando la ecuación definitoria, tomando la derivada parcial de\({ \ln {\tilde{a}}_A\ }\) con respecto a la temperatura, y haciendo uso de la ecuación de Gibbs-Helmholtz:

\[\begin{aligned} \left(\frac{\partial \ln \tilde{a}_A}{\partial T} \right)_P & =\left[\frac{\partial }{\partial T}\left(\frac{{\mu }_A}{RT}-\frac{ \widetilde{\mu }^o_A}{RT}\right)\right]_P \\ ~ & =\frac{1}{R}\left[ \left(\frac{\partial \left({\mu }_A/T \right)}{\partial T}\right)_P- \left(\frac{\partial \left( \widetilde{\mu }^o_A/T\right)}{\partial T}\right)_P\right] \\ ~ & =-\frac{\overline{H}_A}{RT^2}+\frac{\tilde{H}^o_A}{RT^2} \end{aligned}\]

\({\overline{H}}_A\)es la entalpía molar parcial del componente\(A\) ya que está presente en el sistema. \({\tilde{H}}^o_A\)es la entalpía molar parcial del componente\(A\) en su estado estándar de actividad. Dado que este estado estándar no necesita corresponder a ningún sistema real,\({\tilde{H}}^o_A\) puede ser la entalpía molar parcial de la sustancia en un estado hipotético.

En general, no es posible encontrar\(-\left({\overline{H}}_A-{\tilde{H}}^o_A\right)\) por medición experimental el calor intercambiado en un proceso de un solo paso en el que\(A\) pasa de su estado en el sistema de interés a su estado estándar de actividad. En cambio, diseñamos un ciclo de varios pasos en el que podemos determinar el cambio de entalpía para cada paso. Este ciclo incluye otro estado más de sustancia\(A\), al que llamamos el estado de referencia y cuya entalpía molar designamos como\({\overline{H}}^{ref}_A\). Ideamos este ciclo para encontrar dos cambios de entalpía. Uno es el cambio de entalpía que se produce cuando un mol de\(A\) pasa del sistema de interés al estado de referencia; este cambio de entalpía está representado por la diferencia\(-\left({\overline{H}}_A-{\overline{H}}^{ref}_A\right)\). El otro es el cambio de entalpía que se produce cuando un mol de A pasa del estado estándar de actividad al estado de referencia. Este cambio de entalpía está representado por la diferencia\(-\left({\tilde{H}}^o_A-{\overline{H}}^{ref}_A\right)\). El cambio de entalpía que buscamos es la diferencia entre estas dos diferencias:

\[-\left({\overline{H}}_A-{\tilde{H}}^o_A\right)=-\left({\overline{H}}_A-{\overline{H}}^{ref}_A\right)+\left({\tilde{H}}^o_A-{\overline{H}}^{ref}_A\right)\]

Debido a que elegimos explícitamente el estado de referencia para que estas diferencias sean medibles experimentalmente, es útil introducir aún más terminología. Definimos la entalpía molar parcial relativa de la sustancia\(A\)\({\overline{L}}_A\), como la diferencia entre la entalpía molar parcial de\(A\) en el estado de interés\({\overline{H}}_A\), y la entalpía molar parcial de A en el estado de referencia,\({\overline{H}}^{ref}_A\) es decir,\({\overline{L}}_A={\overline{H}}_A-{\overline{H}}^{ref}_A\) y\({\tilde{L}}^o_A={\tilde{H}}^o_A-{\overline{H}}^{ref}_A\) donde\({\tilde{L}}^o_A\) está la entalpía molar parcial relativa de la sustancia\(A\) en el estado estándar de actividad. Claramente, los valores de\({\overline{L}}_A\) y\({\tilde{L}}^o_A\) dependen de la elección del estado de referencia. Elegimos el estado de referencia para que\({\overline{L}}_A\) y se\({\tilde{L}}^o_A\) pueda medir directamente. La cantidad que debemos evaluar experimentalmente para poder encontrar se\({\left({\partial { \ln {\tilde{a}}_A\ }}/{\partial T}\right)}_P\) convierte en

\[-\left({\overline{H}}_A-{\tilde{H}}^o_A\right)=-\left({\overline{L}}_A-{\tilde{L}}^o_A\right)\]

Para ver cómo se puede dar efecto práctico a estas ideas y definiciones, consideremos una solución binaria que comprenda una concentración relativamente baja de soluto,\(A\), en un disolvente,\(B\), a una presión fija, normalmente una barra. Suponemos que puro\(A\) es un sólido y puro\(B\) es un líquido en el rango de temperatura de interés. Necesitamos elegir un estado estándar de actividad y un estado de referencia de entalpía para cada sustancia. Las opciones más generalmente útiles utilizan el concepto de una solución infinitamente diluida. En una solución infinitamente diluida,\(A\) las moléculas se dispersan tan completamente que solo pueden interactuar con\(B\) las moléculas. En consecuencia, la energía de las\(A\) moléculas no puede cambiar si se agrega disolvente puro adicional (inicialmente a la misma temperatura y presión). Operacionalmente entonces, podemos reconocer una solución infinitamente diluida mezclándola con disolvente puro adicional; si no se debe intercambiar calor con el entorno para mantener constante la temperatura, la solución original se diluye infinitamente.

Para el disolvente, el concepto de una solución infinitamente diluida da lugar a las siguientes opciones, que se muestran esquemáticamente en la Figura 3:

Figura 3. Ciclos que relacionan la entalpía molar de un disolvente con sus entalpías molares en el líquido puro, en un estado estándar de actividad y en un estado estándar de entalpía.

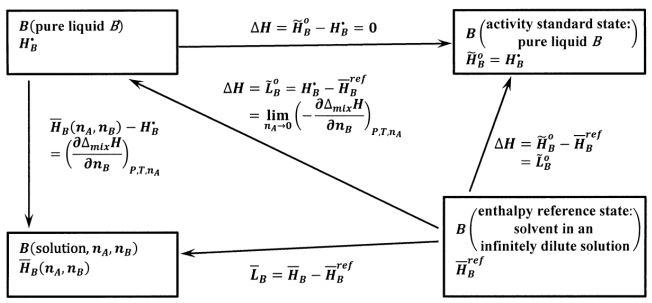
Para el estado estándar de actividad del solvente,\(B\), elegimos líquido puro\(B\). Entonces, la actividad del líquido puro\(B\) es unidad a cualquier temperatura. Dejando\({\tilde{H}}^o_B\) ser la entalpía molar parcial de\(B\) en el estado estándar de actividad y\(H^{\textrm{⦁}}_B\) ser la entalpía molar de líquido puro\(B\), tenemos\({\tilde{H}}^o_B=H^{\textrm{⦁}}_B\).

Para el estado de referencia de entalpía del disolvente, elegimos\(B\) en una solución infinitamente diluida. Representamos la entalpía molar parcial de\(B\) en esta solución infinitamente diluida por\({\overline{H}}^{ref}_B\).

Para el soluto, la solución infinitamente diluida implica las siguientes opciones, que se muestran esquemáticamente en la Figura 4:

Para el estado estándar de actividad del soluto, elegimos la solución hipotética en la que la concentración de\(A\) es un molal, y la actividad de\(A\) es unidad, pero todos los efectos de las interacciones intermoleculares son los mismos que están en una solución infinitamente diluida. Representamos la entalpía molar parcial de\(A\) en el estado estándar de actividad por\({\tilde{H}}^o_A\).

Para el estado de referencia de entalpía del soluto, elegimos la solución infinitamente diluida y designamos la entalpía molar parcial de\(A\) en este estado de referencia por\({\overline{H}}^{ref}_A\). Dado que todas las interacciones intermoleculares son las mismas en el estado de referencia de entalpía que en el estado estándar de actividad, no puede haber cambio de energía cuando un mol de\(A\) va de uno de estos estados al otro. De ello se deduce que\({\tilde{H}}^o_A={\overline{H}}^{ref}_A\).

De estas elecciones se deduce que las entalpías molares parciales relativas de\(A\) y\(B\) en sus estados estándar de actividad son\({\tilde{L}}^o_A={\tilde{H}}^o_A-{\overline{H}}^{ref}_A=0\) y

\[{\tilde{L}}^o_B={\tilde{H}}^o_B-{\overline{H}}^{ref}_B={\mathop{\mathrm{lim}}_{n_A\to 0} {\left(-\frac{\partial {\Delta }_{mix}H}{\partial n_B}\right)}_{P,T,n_A}\ }\]

El proceso relevante para el cual podemos medir un cambio de entalpía es la mezcla isotérmica de\(n_A\) moles de sólido puro\(A\) con\(n_B\) moles de líquido puro\(B\) para formar una solución:

\[{n_AA\left(\mathrm{pure\ solid}\right)+n}_BB\left(\mathrm{pure\ liquid}\right) \begin{array}{c} {\Delta }_{mix}H \\ \to \\ \end{array} {A}/{B\left(\mathrm{solution},\ n_A,n_B\right)}\]

Dejando que la entalpía de mezcla sea\({\Delta }_{mix}H\) y la entalpía de la solución resultante sea\(H\), tenemos

\[H={\Delta }_{mix}H+n_AH^{\textrm{⦁}}_A+n_BH^{\textrm{⦁}}_B\]

Entonces

\[{\overline{H}}_A={\left(\frac{\partial H}{\partial n_A}\right)}_{PT}={\left(\frac{\partial {\Delta }_{mix}H}{\partial n_A}\right)}_{PT}+H^{\textrm{⦁}}_A\]

y

\[{\overline{H}}_B={\left(\frac{\partial H}{\partial n_B}\right)}_{PT}={\left(\frac{\partial {\Delta }_{mix}H}{\partial n_B}\right)}_{PT}+H^{\textrm{⦁}}_B\]donde, por supuesto,\(H\),\({\Delta }_{mix}H\),\({\overline{H}}_A\), y\({\overline{H}}_B\) son todas funciones de\(n_A\) y\(n_B\). Las entalpías molares parciales en los estados de referencia son los valores limitantes de\({\overline{H}}_A\) y\({\overline{H}}_B\) como\(n_A\to 0\). Es decir,

\[{\overline{H}}^{ref}_A={\mathop{\mathrm{lim}}_{n_A\to 0} {\left(\frac{\partial {\Delta }_{mix}H}{\partial n_A}\right)}_{P,T,n_B}\ }+H^{\textrm{⦁}}_A\]y\[{\overline{H}}^{ref}_B={\mathop{\mathrm{lim}}_{n_B\to 0} {\left(\frac{\partial {\Delta }_{mix}H}{\partial n_B}\right)}_{P,T,n_A}\ }+H^{\textrm{⦁}}_B\]

Cuando basamos los estados de referencia de entalpía en la solución infinitamente diluida, encontramos para el soluto

\[-\left({\overline{H}}_A-{\tilde{H}}^o_A\right)=-\left({\overline{H}}_A-{\overline{H}}^{ref}_A\right)+\left({\tilde{H}}^o_A-{\overline{H}}^{ref}_A\right)\]\[=-\left({\overline{L}}_A-{\tilde{L}}^o_A\right)=-{\overline{L}}_A=-{\left(\frac{\partial {\Delta }_{mix}H}{\partial n_A}\right)}_{P,T,n_B}+{\mathop{\mathrm{lim}}_{n_A\to 0} {\left(\frac{\partial {\Delta }_{mix}H}{\partial n_A}\right)}_{P,T,n_B}\ }\]

y para el solvente

\[-\left({\overline{H}}_B-{\tilde{H}}^o_B\right)=-\left({\overline{H}}_B-{\overline{H}}^{ref}_B\right)+\left({\tilde{H}}^o_B-{\overline{H}}^{ref}_B\right)=-\left({\overline{L}}_B-{\tilde{L}}^o_B\right)=-{\left(\frac{\partial {\Delta }_{mix}H}{\partial n_B}\right)}_{P,T,n_A}\]

La dependencia de la temperatura de las actividades se convierte en

\[{\left(\frac{\partial { \ln {\tilde{a}}_A\ }}{\partial T}\right)}_P=\frac{1}{RT^2}\left[-{\left(\frac{\partial {\Delta }_{mix}H}{\partial n_A}\right)}_{P,T,n_B}+{\mathop{\mathrm{lim}}_{n_A\to 0} {\left(\frac{\partial {\Delta }_{mix}H}{\partial n_A}\right)}_{P,T,n_B}\ }\right]\]

y\[{\left(\frac{\partial { \ln {\tilde{a}}_B\ }}{\partial T}\right)}_P=-\frac{1}{RT^2}{\left(\frac{\partial {\Delta }_{mix}H}{\partial n_B}\right)}_{P,T,n_A}\]

A una buena primera aproximación, podemos medir\({\Delta }_{mix}H\) en función de la composición a una sola temperatura, determinar\({\overline{L}}_A\) y\({\overline{L}}_B-{\tilde{L}}^o_B\) a esa temperatura, y asumir que estos valores son independientes de la temperatura. Para un tratamiento más exacto, podemos medir\({\Delta }_{mix}H\) en función de la composición a varias temperaturas y encontrar\({\overline{L}}_A\) y\({\overline{L}}_B-{\tilde{L}}^o_B\) como funciones de la temperatura. Resulta útil definir la capacidad calorífica molar parcial relativa de\(A\), a la que le damos el símbolo,\({\overline{J}}_A\), como la derivada de temperatura de\({\overline{L}}_A\):

\[{\overline{J}}_A={\left(\frac{\partial {\overline{L}}_A}{\partial T}\right)}_P\]

Para ilustrar el uso de estas ideas, supongamos que medimos la entalpía de mezcla de soluto\(A\) en 1 kg de agua (solvente\(B\)). Hacemos esta medición para varias cantidades de\(A\) a cada una de varias temperaturas entre 273.15 K y 293.15 K. Para cada experimento de esta serie,\(n_B\) es 55.51 mol y\(n_A\) es igual a la molalidad de\(A\),\(\underline{m}\), en la solución. Ajustamos los datos experimentales a ecuaciones empíricas. Supongamos que la entalpía de los datos de mezcla a cualquier temperatura dada se describe adecuadamente por la ecuación\({\Delta }_{mix}H={\alpha }_1\underline{m}+{\alpha }_2{\underline{m}}^2\) y eso\({\alpha }_1\) y\({\alpha }_2\) dependen linealmente de\(T\) acuerdo con

\[{\alpha }_1={\beta }_{11}+{\beta }_{12}\left(T-273.15\right)\]y

\[{\alpha }_2={\beta }_{21}+{\beta }_{22}\left(T-273.15\right)\]

Entonces

\[{\left(\frac{\partial {\Delta }_{mix}H}{\partial n_A}\right)}_{P,T,n_B}={\left(\frac{\partial {\Delta }_{mix}H}{\partial \underline{m}}\right)}_{P,T,n_B}={\alpha }_1+2{\alpha }_2\underline{m}\]

y

\[{\mathop{\mathrm{lim}}_{n_A\to 0} {\left(\frac{\partial {\Delta }_{mix}H}{\partial n_A}\right)}_{P,T,n_B}\ }={\alpha }_1\]

para que

\[{\overline{L}}_A={\left(\frac{\partial {\Delta }_{mix}H}{\partial n_A}\right)}_{P,T,n_B}-{\mathop{\mathrm{lim}}_{n_A\to 0} {\left(\frac{\partial {\Delta }_{mix}H}{\partial n_A}\right)}_{P,T,n_B}\ }=2{\alpha }_2\underline{m}\]

y

\[\left(\frac{\partial \ln \tilde{a}_A}{\partial T}\right)_P=-\frac{\overline{L}_A}{RT^2}=-\frac{2{\alpha }_2\underline{m}}{RT^2}\]

y

\[{\overline{J}}_A={\left(\frac{\partial {\overline{L}}_A}{\partial T}\right)}_P=2\underline{m}{\left(\frac{\partial {\alpha }_2}{\partial T}\right)}_P=2\underline{m}{\beta }_{22}\]

En los experimentos de este ejemplo ilustrativo,\(n_B\) es constante. Esto podría hacer parecer que tendríamos que hacer un conjunto adicional de experimentos, un conjunto en el que\(n_B\) es variado, con el fin de encontrar\({\overline{L}}_B\),\({\left({\partial { \ln {\tilde{a}}_B\ }}/{\partial T}\right)}_P\), y\({\overline{J}}_B\). Sin embargo, este no es el caso. Desde\({\overline{L}}_A\) y\({\overline{L}}_B\) son cantidades molares parciales, tenemos

\[n_Ad{\overline{L}}_A+n_Bd{\overline{L}}_B=0\]para que\[d{\overline{L}}_B=-\left(\frac{n_A}{n_B}\right)d{\overline{L}}_A\]

y podemos encontrar\({\overline{L}}_B\) desde

\[\overline{L}_B\left(\underline{m}\right)-\overline{L}_B\left(0\right)=\overline{L}_B\left(\underline{m}\right)=\int^{\underline{m}}_0 -\left(\frac{2\underline{m}{\alpha }_2}{55.51}\right)d\underline{m}=-\frac{\underline{m}^2{\alpha }_2}{55.51}\]

y

\[\overline{J}_B= \left(\frac{\partial \overline{L}_B}{\partial T}\right)_P=-\frac{\underline{m}^2}{55.51} \left(\frac{\partial {\alpha }_2}{\partial T} \right)_{P,n_A}=-\frac{\underline{m}^2{\beta }_{22}}{55.51}\]