15.7: Potencial, Actividad y Equilibrio Químicos
- Page ID
- 73858
Cuando elegimos un estado estándar para la actividad de una sustancia, queremos que el potencial químico que calculamos a partir de la actividad medida de una sustancia en un sistema particular sea la diferencia de energía libre de Gibbs para la formación de la sustancia en ese sistema a partir de sus elementos constitutivos en sus estados estándar.
Así, debemos poder medir el cambio libre de Gibbs para el proceso que produce la sustancia en su estado estándar de actividad a partir de sus elementos constituyentes; esta es la cantidad que designamos como\({\Delta }_f{\tilde{G}}^o\left(A,ss\right)={\widetilde{\mu }}^o_A\). También debemos poder medir la diferencia entre el potencial químico de la sustancia en este estado estándar y su potencial químico en el sistema de interés; esta es la cantidad que designamos como\(RT{ \ln {\tilde{a}}_A\ }\). La suma\[{\mu }_A={\widetilde{\mu }}^o_A+RT{ \ln {\tilde{a}}_A\ }\]
es entonces el cambio de energía libre de Gibbs deseado para la formación de la sustancia en el sistema de interés.
Cuando es conveniente elegir el estado estándar de actividad para que sea el estado estándar del líquido puro o el sólido puro, tenemos
\[{\Delta }_f{\tilde{G}}^o\left(A,ss\right)={\widetilde{\mu }}^o_A={\Delta }_fG^o\left(A,\ell \right)\]o\[{\Delta }_f{\tilde{G}}^o\left(A,ss\right)={\widetilde{\mu }}^o_A={\Delta }_fG^o\left(A,s\right)\]
Para otras opciones, es posible que no podamos medir la diferencia entre el potencial químico de la sustancia en el estado estándar de actividad y el de sus elementos constituyentes en sus estados estándar; es decir, el valor de\({\Delta }_f{\tilde{G}}^o\left(A,ss\right)={\widetilde{\mu }}^o_A\) puede ser desconocido. Sin embargo, podemos describir los cambios de energía libre de Gibbs en un ciclo que va desde los elementos en sus estados estándar hasta las especies químicas en el sistema de equilibrio y espalda.
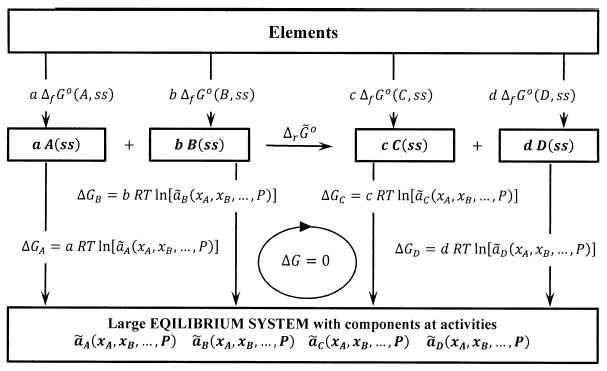
Para la reacción\(aA+bB\to cC+dD\), este ciclo se muestra en la Figura 3. Sumando los cambios de energía libres de Gibbs en el sentido de las agujas del reloj alrededor de este ciclo, tenemos
\[0=c\ {\Delta }_f{\tilde{G}}^o\left(C,ss\right)+d\ {\Delta }_f{\tilde{G}}^o\left(D,ss\right)-a\ {\Delta }_f{\tilde{G}}^o\left(A,ss\right)-b\ {\Delta }_f{\tilde{G}}^o\left(B,ss\right)\]\[+c\ RT{ \ln {\tilde{a}}^c_C\ }+d\ RT{ \ln {\tilde{a}}^d_D\ }-a\ RT{ \ln {\tilde{a}}^a_A\ }-b\ RT{ \ln {\tilde{a}}^b_B\ }\]
Escribiendo\({\Delta }_r{\tilde{G}}^o\) para enfatizar que el cambio de energía libre de Gibbs estándar para la reacción es ahora una diferencia entre los potenciales químicos de los reactivos y productos en sus estados estándar de actividad, tenemos
\[{\Delta }_r{\tilde{G}}^o=c\ {\Delta }_f{\tilde{G}}^o\left(C,ss\right)+d\ {\Delta }_f{\tilde{G}}^o\left(D,ss\right)-a\ {\Delta }_f{\tilde{G}}^o\left(A,ss\right)-b\ {\Delta }_f{\tilde{G}}^o\left(B,ss\right)={\Delta }_r{\widetilde{\mu }}^o\]
y la ecuación para el cambio de energía libre de Gibbs alrededor del ciclo se convierte en
\[{\Delta }_r{\tilde{G}}^o={\Delta }_r{\widetilde{\mu }}^o=-RT{ \ln \frac{{\tilde{a}}^c_C{\tilde{a}}^d_D}{{\tilde{a}}^a_A{\tilde{a}}^b_B}\ }\]
Dado que la reacción química está en equilibrio, el término de actividades es constante. Tenemos
\[K_a=\frac{{\tilde{a}}^c_C{\tilde{a}}^d_D}{{\tilde{a}}^a_A{\tilde{a}}^b_B}\]
y\[K_a=\mathrm{exp}\left(\frac{-{\Delta }_r{\tilde{G}}^o}{RT}\right)=\mathrm{exp}\left(\frac{-{\Delta }_r{\widetilde{\mu }}^o}{RT}\right)\]
Anexamos el subíndice, “\(a\)”, para indicar que la constante de equilibrio,\(K_a\), se expresa en términos de las actividades de las sustancias reaccionantes. Este ciclo demuestra la lógica subyacente para nuestro cálculo de\(K_a\) desde nuestra definición de actividad\({\mu }_A={\widetilde{\mu }}^o_A+RT{ \ln {\tilde{a}}_A\ }\), nuestra definición de\({\Delta }_r\mu\), y el hecho de que
\[{\Delta }_r\mu =\sum^{\omega }_{j=1}{{\mu }_j{\nu }_j=0}\]
es un criterio de equilibrio.
Introduciendo coeficientes de actividad, tenemos
\[K_a=\frac{{\tilde{a}}^c_C{\tilde{a}}^d_D}{{\tilde{a}}^a_A{\tilde{a}}^b_B}=\left(\frac{c^c_Cc^d_D}{c^a_Ac^b_B}\right)\left(\frac{{\gamma }^c_C{\gamma }^d_D}{{\gamma }^a_A{\gamma }^b_B}\right)\]
Cuando conocemos\(K_a\) y podemos estimar los coeficientes de actividad, podemos predecir las propiedades termodinámicas de un sistema cuyas concentraciones de componentes son conocidas. En general, determinar\(K_a\) y los coeficientes de actividad es más difícil que determinar las concentraciones de equilibrio. En intervalos estrechos de concentraciones suele ser adecuado suponer que la función del coeficiente de actividad,
\[K_{\gamma }=\frac{{\gamma }^c_C{\gamma }^d_D}{{\gamma }^a_A{\gamma }^b_B}\]
es aproximadamente constante. Cuando este es el caso, la función de concentración,
\[K_c=\frac{c^c_Cc^d_D}{c^a_Ac^b_B}\]
es aproximadamente constante. Entonces, una medición directa de\(K_c\) en un sistema de equilibrio permite predecir la posición del equilibrio en otros sistemas similares.
La relación entre la constante de equilibrio y el cambio de energía libre estándar de Gibbs para una reacción es extremadamente útil. Si podemos calcular el cambio estándar de energía libre de Gibbs a partir de valores tabulados, podemos encontrar la constante de equilibrio y predecir la posición de equilibrio para un sistema en particular. Por el contrario, si podemos medir la constante de equilibrio, podemos encontrar el cambio de energía libre estándar de Gibbs,\({\Delta }_r{\tilde{G}}^o\).
Esto nos devuelve a un reto central en nuestro desarrollo. Ahora tenemos relaciones rigurosas entre la energía libre de Gibbs y la fugacidad o actividad de una sustancia. Para utilizar estas relaciones, debemos ser capaces de relacionar la fugacidad o actividad con la concentración de una sustancia en cualquier sistema en particular que queramos estudiar. Para muchos sistemas comunes, esto es difícil. En el Capítulo 16, discutimos algunos enfoques básicos para lograrlo.


