16.7: Encontrar la actividad de un soluto a partir de la actividad del solvente

Hemos visto que la actividad de cualquier componente de un sistema de equilibrio contiene información sobre las actividades de todos los demás componentes. Desde

\[d\mu =-\overline{S}dT+\overline{V}P+RTd{ \ln \tilde{a}\ }\nonumber \]

y la ecuación de Gibbs-Duhem, podemos encontrar una relación general entre las actividades. Sustituyendo\(d{\mu }_A\) y\(d{\mu }_B\) en la ecuación de Gibbs-Duhem, tenemos, para una solución de dos componentes,

\[ \begin{align*} -SdT+VdP &=n_Ad{\mu }_A+n_Bd{\mu }_B \\[4pt]&= n_A\left(-{\overline{S}}_AdT+{\overline{V}}_AP+RTd{ \ln {\tilde{a}}_A\ }\right)+n_B\left(-{\overline{S}}_BdT+{\overline{V}}_BP+RTd{ \ln {\tilde{a}}_B\ }\right) \\[4pt]&= -\left(n_A{\overline{S}}_A+n_B{\overline{S}}_B\right)dT + \left(n_A{\overline{V}}_A+n_B{\overline{V}}_B\right)dP + n_ARTd{ \ln {\tilde{a}}_A\ }+n_BRTd{ \ln {\tilde{a}}_B\ }\end{align*}\]

Desde\(S=n_A{\overline{S}}_A+n_B{\overline{S}}_B\) y\(V=n_A{\overline{V}}_A+n_B{\overline{V}}_B\), esto simplifica a

\[0=n_Ad{ \ln {\tilde{a}}_A\ }+n_Bd{ \ln {\tilde{a}}_B\ }\nonumber \]

o, dividiendo por\(n_A+n_B\),

\[0=y_Ad{ \ln {\tilde{a}}_A\ }+y_Bd{ \ln {\tilde{a}}_B\ }\nonumber \]

Por simplicidad, consideremos un sistema en el que un soluto no volátil,\(A\), se disuelve en un disolvente volátil,\(B\). Midiendo la presión del sistema y aplicando las ecuaciones que desarrollamos en la Sección 16.1 para componente volátil\(A\) al disolvente volátil\(B\),, en el presente sistema, podemos determinar la actividad del disolvente,\(B\). Usemos fracciones molares para medir concentraciones y tomar líquido puro\(B\) a su presión de vapor de equilibrio como estado estándar de actividad tanto para la fase líquida como para la fase gaseosa\(B\). Cuando\(B\) está en su estado estándar, tenemos\(x_A=0\),\(x_B=1\), y\({\overline{V}}_B\left(g\right)={\overline{V}}^{\textrm{⦁}}_B\left(g\right)\). Entonces, dado que el soluto es no volátil, podemos determinar la actividad del disolvente,\(B\), a partir de la presión del sistema. Tenemos

\[{ \ln \left[{\tilde{a}}_B\left(P,y_A,y_B\right)\right]=\ }RT{ \ln \left[\frac{P}{P^{\textrm{⦁}}_B}\right]-\int^P_{P^{\textrm{⦁}}_B}{\left(\frac{{\overline{V}}^{\textrm{⦁}}_B \left(g\right)}{RT}-\frac{1}{P}\right)}\ }dP\nonumber \]

Suponiendo que la integral hace una contribución insignificante a la actividad, tenemos

\[{\tilde{a}}_B\left(P,y_A,y_B\right)={\tilde{a}}_B=y_B\gamma_B\left(P,y_A,y_B\right)=\frac{P}{P^{\textrm{⦁}}_B}\nonumber \](solvente)

para que

\[\gamma_B\left(P,y_A,y_B\right)=\gamma_B=\frac{P}{y_BP^{\textrm{⦁}}_B}\nonumber \](solvente)

Dado que la concentración en fase gaseosa de\(A\) es inconmensurablemente pequeña, debemos determinar su actividad indirectamente. Que el estado estándar para la actividad del soluto sea el hipotético líquido puro\(y_A=1\), cuya presión de vapor de equilibrio es igual a la constante de soluto de la ley de Henry\(A\). (Podemos determinar la actividad del soluto sin medir su constante de la ley de Henry). Tenemos

\[{\mu }_A\left(P,y_A,y_B\right)={\widetilde{\mu }}^o_A\left(Hyp\ \ell ,{\textrm{ҝ}}_A\right)+RT{ \ln \left[{\tilde{a}}_A\left(P,y_A,y_B\right)\right]\ }\nonumber \]

donde

\[{\tilde{a}}_A\left(P,y_A,y_B\right)={\tilde{a}}_A=y_A\gamma_A\nonumber \](soluto)

Dado que somos capaces de medir la actividad del solvente, podemos determinar la actividad del soluto a partir de la relación\(0=y_Ad{ \ln {\tilde{a}}_A\ }+y_Bd{ \ln {\tilde{a}}_B\ }\). Reordenando, tenemos

\[d{ \ln {\tilde{a}}_A\ }=-\frac{y_B}{y_A}d{ \ln {\tilde{a}}_B\ }=-\left(\frac{{1-y}_A}{y_A}\right)d{ \ln {\tilde{a}}_B\ }\nonumber \]

Para dos soluciones en las que las fracciones molares de\(A\) son\(y_A\) y\(y^{\#}_A\), y en las que las actividades de\(A\) y\(B\) son\({\tilde{a}}_A\)\({\tilde{a}}_B\)\({\tilde{a}}^{\#}_A\),\({\tilde{a}}^{\#}_B\), y, tenemos

\[ \ln \frac{\tilde{a}_A}{\tilde{a}^{\#}_A}=-\int^{y_A}_{y^{\#}_A} \left(\frac{1-y_A}{y_A}\right)d \ln \tilde{a}_B\nonumber \]

Gráficamente, la integral es el área bajo una parcela de\(-{\left(1-y_A\right)}/{y_A}\) versus\({ \ln {\tilde{a}}_B\ }\), de\(y^{\#}_A\) a\(y_A\).

Por lo general, nos interesan soluciones para las cuales\(y_A\ll y_B\). En el límite a medida que la solución se vuelve muy diluida, la actividad, fracción molar, y coeficiente de actividad del disolvente,\(B\), todos se acercan a la unidad:\({\tilde{a}}_B\to 1\)\(y_B\to 1\),, y\(\gamma_B\to 1\). La actividad del soluto,\(A\), se acerca a la fracción molar de\(A\). Por experiencia, el enfoque es asintótico: a medida que la fracción molar se acerca a cero,\(y_A\to 0\), el coeficiente de actividad del soluto se acerca a la unidad\(\gamma_A\to 1\),, y lo hace asintóticamente, así que\({\tilde{a}}_A\to y_A\). Para soluciones diluidas,\({ \ln {\tilde{a}}_A\to -\infty \ }\) y\({ \ln \gamma_A\to 0\ }\) asintóticamente. En consecuencia,

\[{\mathop{\mathrm{lim}}_{y_A\to 0} \left(d{ \ln \gamma_A\ }\right)\ }=0\nonumber \]

Debido a que el coeficiente de actividad se acerca a un límite finito mientras que la actividad no lo hace, podemos expresar la actividad del soluto simplemente encontrando el coeficiente de actividad del soluto. Desde\({\tilde{a}}_A=y_A\gamma_A\) y\({\tilde{a}}_B=y_B\gamma_B=\left(1-y_A\right)\gamma_B\), tenemos

\[\begin{align*} 0 &=y_Ad{ \ln {\tilde{a}}_A\ }+y_Bd{ \ln {\tilde{a}}_B\ } \\[4pt] &=y_Ad{ \ln y_A\gamma_A\ }+y_Bd{ \ln y_B\gamma_B\ }=y_Ad{ \ln y_A\ }+y_Ad{ \ln \gamma_A\ }+y_Bd{ \ln y_B\ }+y_Bd{ \ln \gamma_B\ } \\[4pt]&=\left(dy_A+dy_B\right)+y_Ad{ \ln \gamma_A\ }+y_Bd{ \ln \gamma_B\ }=y_Ad{ \ln \gamma_A\ }+y_Bd{ \ln \gamma_B\ }\end{align*}\]

(Ya que\(y_A+y_B=1\), tenemos\({dy}_A+{dy}_B=0\).) Podemos reorganizar esto para

\[d{ \ln \gamma_A\ }=-\left(\frac{{1-y}_A}{y_A}\right)d{ \ln \gamma_B\ }\nonumber \]

A medida que la concentración de soluto se acerca a cero,\({\left(1-y_A\right)}/{y_A}\) se vuelve arbitrariamente grande. Sin embargo, ya que\({\mathop{\mathrm{lim}}_{y_A\to 0} \left(d{ \ln \gamma_A\ }\right)\ }=0\), se deduce que

\[{\mathop{\mathrm{lim}}_{y_A\to 0} d{ \ln \gamma_B\ }\ }=0\nonumber \]

Vemos que el coeficiente de actividad solvente también se acerca a la unidad asintóticamente ya que la concentración de soluto va a cero. El coeficiente de actividad del soluto en cualquiera\(y_A>0\) viene dado entonces por

\[\int^{y_A}_0 d \ln \left[\gamma_A\left(y_A\right)\right] \ln \left[\gamma_A\left(y_A\right)\right] \int^{y_A}_0 -\left(\frac{1-y_A}{y_A}\right)d \ln \left[\gamma_B\left(y_A\right)\right]\nonumber \]

Figura 6. Representación gráfica de\(\ln \gamma\) para el soluto cuando se conoce\(\gamma\) del disolvente.

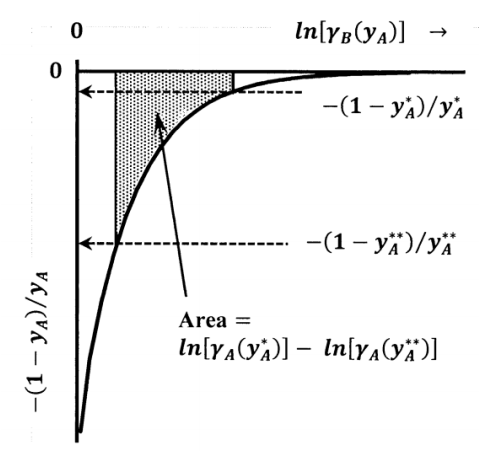
Como se esboza en la Figura 6, esta última integral es el área bajo una gráfica de\({-\left(1-y_A\right)}/{y_A}\) versus\({ \ln \left[\gamma_B\left(y_A\right)\right]\ }\), entre\(y_A=0\) y\(y_A\). Ya que\(\gamma_A\left(y_A\right)\to 1\) como\(y_A\to 0\), esta integral debe permanecer finita aunque\({-\left(1-y_A\right)}/{y_A}\to -\infty\) como\(y_A\to 0\). Esto puede ocurrir, porque\({\mathop{\mathrm{lim}}_{y_A\to 0} d{ \ln \gamma_B\ }\ }=0\), como observamos anteriormente. Sin embargo, el hecho de que el integrando no esté limitado puede limitar la precisión de la integración necesaria. Para una medición precisa del coeficiente de actividad de soluto, es importante obtener datos de solvente-actividad a la concentración de soluto más baja posible.

La situación más deseable es recolectar datos de actividad solvente hasta concentraciones de soluto en las que el coeficiente de actividad solvente,\(\gamma_B\), se convierte en unidad. Si\(\gamma_B\left(y^{\#}_A\right)=1\) cuando la concentración de soluto es\(y^{\#}_A\), se\({ \ln \left[\gamma_A\left(y_A\right)\right]\ }\) puede evaluar con\(y^{\#}_A\), en lugar de cero, como límite inferior de integración. En algunos casos,\({ \ln \left[\gamma_A\left(y^{\triangle }_A\right)\right]\ }\) puede conocerse a partir de alguna otra medición a una concentración particular,\(y^{\triangle }_A\); si es así, podemos encontrar\({ \ln \left[\gamma_A\left(y_A\right)\right]\ }\) llevando a cabo la integración numérica entre los límites\(y^{\triangle }_A\) y\(y_A\).

Si la medición de\(\gamma_B\) no puede extenderse a valores de\(y_A\) a los cuales\(\gamma_B\left(y_A\right)=1\), debemos encontrar una función empírica, llamarla\(f\left(y_A\right)\), que se ajuste a los valores experimentales de\({ \ln \left[\gamma_B\left(y_A\right)\right]\ }\), para los valores más pequeños de\(y_A\). (Es decir, la función empírica es\({f\left(y_A\right)\mathrm{=ln} \left[\gamma_B\left(y_A\right)\right]\ }\).) El diferencial de\(f\left(y_A\right)\) es entonces un modelo matemático para\(d{ \ln \left[\gamma_B\left(y_A\right)\right]\ }\) sobre la región de bajas concentraciones de soluto. Dejando\(y^{\#}_A\) ser la concentración de soluto más pequeña para la que se puede determinar la actividad solvente, podemos integrar, utilizando la función para\(d{ \ln \left[\gamma_B\left(y_A\right)\right]\ }\) que derivamos de este modelo, para estimar\({ \ln \left[\gamma_B\left(y^{\#}_A\right)\right]\ }\). La incertidumbre sobre la precisión del modelo matemático se convierte en una fuente significativa de incertidumbre en los valores calculados de\(\gamma_A\).

Por supuesto, si podemos encontrar una función analítica que proporcione un buen modelo matemático para todos los datos de solvente-actividad, el diferencial de esta función se puede utilizar en la integral para evaluar en\({ \ln \left[\gamma_A\left(y_A\right)\right]\ }\) todo el rango de los datos experimentales. Si es necesario, la evaluación de esta integral se puede lograr utilizando métodos numéricos.

Es esencial que cualquier función empírica,\({f\left(y_A\right)\mathrm{=ln} \left[\gamma_B\left(y_A\right)\right]\ }\), tenga las propiedades matemáticas correctas sobre el rango de concentración al que se aplica. Si se va a utilizar para extender la integración a\(y_A=0\),\(f\left(y_A\right)\) debe satisfacer\(f\left(0\right)=0\) y\(df\left(0\right)=0\). Esta es una condición importante. Por ejemplo, considere la aproximación

\[f\left(y_A\right)={ \ln \left[\gamma_B\left(y_A\right)\right]\ }=c_By^{{\alpha }_B}_A\nonumber \]

Este modelo da

\[\frac{d{ \ln \left[\gamma_A\left(y_A\right)\right]\ }}{dy_A}={-\left(1-y_A\right)c}_B{\alpha }_By^{{\alpha }_B-2}_A\nonumber \]y\[{\mathop{\mathrm{lim}}_{y_A\to 0} \frac{d{ \ln \left[\gamma_A\left(y_A\right)\right]\ }}{dy_A}\ }=0\nonumber \]

requiere\({\alpha }_B>2\).