16.15: Coeficientes de actividad del disolvente a partir de mediciones de depresión en el punto

El análisis de la depresión del punto de congelación que presentamos en la Sección 16.11 introduce una serie de supuestos simplificadores. Ahora emprendemos un análisis más riguroso de este fenómeno. Este análisis es de importancia práctica. Medir la depresión del punto de congelación de una solución es una manera de determinar la actividad y el coeficiente de actividad del componente disolvente. Como vemos en la Sección 16.7, si tenemos coeficientes de actividad para el disolvente en un rango de concentraciones de soluto, podemos usar la ecuación de Gibbs-Duhem para encontrar coeficientes de actividad para el soluto. Las mediciones de depresión del punto de congelación se han utilizado ampliamente para determinar los coeficientes de actividad de los solutos acuosos midiendo la actividad del agua en sus soluciones.

Al igual que en nuestra discusión anterior sobre la depresión del punto de congelación, el sistema de equilibrio es una solución de soluto\(A\) en disolvente\(B\), que está en equilibrio de fase con disolvente sólido puro\(B\). Nuestro objetivo actual es determinar la actividad del solvente en sus soluciones en el punto de fusión del solvente puro. Habiendo obtenido esta información, podemos usar la relación Gibbs-Duhem para encontrar la actividad del soluto, en función de la concentración de soluto, en el punto de fusión del solvente puro. Una vez que tenemos la actividad del soluto en el punto de fusión del disolvente puro, podemos utilizar los métodos desarrollados en la Sección 14.14 para encontrar la actividad del soluto en una solución a cualquier temperatura superior.

En la Sección 14.14, encontramos la dependencia de la temperatura del logaritmo natural de la actividad química de un componente de una solución. Para una elección particular de estados estándar de actividad y estados de referencia de entalpía, desarrollamos un método para obtener los datos experimentales que necesitamos para aplicar esta ecuación. Por brevedad, vamos a referirnos a estas elecciones como los estados estándar de dilución infinita. Para determinar la actividad de un disolvente en sus soluciones en el punto de fusión del disolvente puro, es útil definir un estado estándar adicional para el disolvente. A temperaturas por debajo del punto de fusión normal, que nuevamente designamos como\(T_F\), dejamos que el estado estándar de actividad del disolvente sea sólido puro\(B\). Por encima del punto de fusión, utilizamos el estado estándar de dilución infinita que definimos en la Sección 14.14; es decir, dejamos que el estado estándar de actividad del solvente sea solvente líquido puro\(B\).

En y por debajo del punto de fusión\(T_F\),, el estado estándar de actividad para el disolvente\(B\),, es sólido puro\(B\). En y por encima del punto de fusión, el estado estándar de actividad para el disolvente es líquido puro\(B\). En el punto de fusión, el disolvente sólido puro está en equilibrio con el disolvente líquido puro, que también es el disolvente en una solución infinitamente diluida. At\(T_F\), los potenciales químicos del estado estándar de actividad del disolvente sólido puro, el disolvente líquido puro y el disolvente en una solución infinitamente diluida son todos iguales. De ello se deduce que el valor que obtenemos para la actividad del disolvente en\(T_F\), para cualquier solución en particular, será el mismo ya sea que lo determinemos a partir de mediciones a continuación\(T_F\) usando el estado estándar sólido puro o a partir de mediciones anteriores\(T_F\) usando la solución infinitamente diluida estado estándar.

Ahora consideremos el potencial químico del solvente líquido\(B\) en una solución cuya composición se especifica por la molalidad del soluto\(A\),\({\underline{m}}_A\), cuando el estado estándar de actividad es sólido puro\(B\). Queremos encontrar este potencial químico a temperaturas en el rango\(T_{fp}<t_f\) >, donde\(T_{fp}\) está el punto de congelación de la solución cuya composición se especifica por\({\underline{m}}_A\). En este rango de temperatura, tenemos

\[{\mu }_B\left(\mathrm{solution},\ {\underline{m}}_A,T\right)\]\[={\widetilde{\mu }}^o_B\left(\mathrm{pure\ solid},\ T\right)+RT{ \ln {\tilde{a}}_B\ }\left(\mathrm{solution},\ {\underline{m}}_A,T\right)\]

Usando la ecuación de Gibbs-Helmholtz, obtenemos

\[{\left(\frac{\partial { \ln {\tilde{a}}_B\ }\left(\mathrm{solution},\ {\underline{m}}_A,T\right)}{\partial T}\right)}_{P,{\underline{m}}_A}\]

\[\ \ \ \ =\frac{-{\overline{H}}_B\left(\mathrm{solution},\ {\underline{m}}_A,T\right)}{RT^2}+\frac{{\tilde{H}}^o_B\left(T\right)}{RT^2}\]\[=\frac{-\left[{\overline{H}}_B\left(\mathrm{solution},\ {\underline{m}}_A,T\right)-{\overline{H}}^{\textrm{⦁}}_B\left(\mathrm{solid},T\right)\right]}{RT^2}\]

donde tenemos\({\tilde{H}}^o_B\left(T\right)={\overline{H}}^{\textrm{⦁}}_B\left(\mathrm{solid},T\right)\), porque el sólido puro\(B\) es el estado estándar de actividad. Utilizando las ideas desarrolladas en la Sección 14.14, podemos utilizar el ciclo termoquímico mostrado en la Figura 10 para evaluar

\[{\overline{H}}_B\left(\mathrm{solution},\ {\underline{m}}_A,T\right)-{\overline{H}}^{\textrm{⦁}}_B\left(\mathrm{solid},T\right)\]

Figura 10. Ciclo de entalpía para la dependencia de la temperatura de\( \ln \tilde{a}_B\).

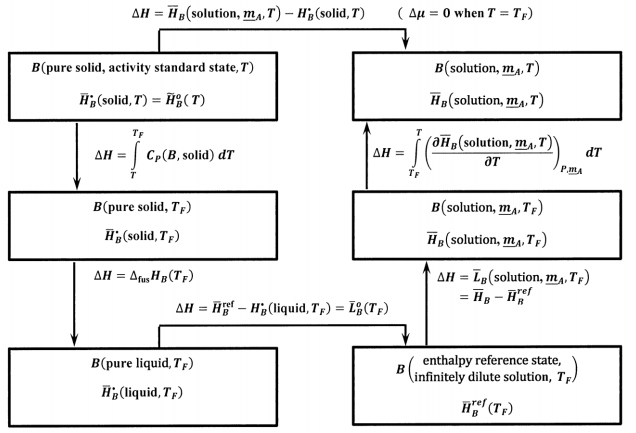
En este ciclo,\({\Delta }_{\mathrm{fus}}{\overline{H}}_B\left(T_F\right)\) se encuentra la entalpía molar de fusión de puro\(B\) en el punto de fusión,\(T_F\). \({\overline{L}}_B\left(\mathrm{solution},\ {\underline{m}}_A,T\right)\)es la entalpía molar parcial relativa de\(B\) at\(T_F\) en una solución cuya composición se especifica por\({\underline{m}}_A\). La única cantidad nueva en este ciclo es

\[\int^T_{T_f}{{\left(\frac{\partial {\overline{H}}_B\left(\mathrm{solution},\ {\underline{m}}_A,T\right)}{\partial T}\right)}_{P,{\underline{m}}_A}dT}\]Podemos usar la entalpía molar parcial relativa de la solución para encontrarla. Por definición,

\[{\overline{L}}_B\left(\mathrm{solution},\ {\underline{m}}_A,T\right)\]\[={\left(\frac{\partial H\left(\mathrm{solution},\ {\underline{m}}_A,T\right)}{\partial n_B}\right)}_{P,T,n_A}-{\overline{H}}^{\mathrm{ref}}_B\left(T\right)\]

o, dejando caer la información entre paréntesis,

\[{\overline{L}}_B={\overline{H}}_B-{\overline{H}}^{\mathrm{ref}}_B\left(T\right)\]

para que\[{\left(\frac{{\partial \overline{L}}_B}{\partial T}\right)}_P={\left(\frac{\partial {\overline{H}}_B}{\partial T}\right)}_P-{\left(\frac{\partial {\overline{H}}^{\mathrm{ref}}_B}{\partial T}\right)}_P\]

En la Sección 14.14 se introduce la capacidad calorífica molar parcial relativa,

\[{\overline{J}}_B\left(T\right)={\left(\frac{{\partial \overline{L}}_B}{\partial T}\right)}_P\]

Dado que la solución infinitamente diluida es el estado de referencia de entalpía para\(B\) en solución, esperamos que la entalpía molar del líquido\(B\) puro sea una buena aproximación a la entalpía molar parcial del líquido\(B\) en el estado de referencia de entalpía. Entonces,\({\left({\partial {\overline{H}}^{\mathrm{ref}}_B}/{\partial T}\right)}_P\) es solo la capacidad calorífica molar del líquido puro\(B\),\(C_P\left(B,\mathrm{liquid},T\right)\). (Ver problema 16-11.) Nos encontramos

\[{\left(\frac{\partial {\overline{H}}_B}{\partial T}\right)}_P={\overline{J}}_B\left(T\right)+C_P\left(B,\mathrm{liquid},T\right)\]

Usando este resultado, la entalpía cambia alrededor del ciclo en la Figura 10 rendimiento

\[{\overline{H}}_B\left(\mathrm{solution},\ {\underline{m}}_A,T\right)-{\overline{H}}^{\textrm{⦁}}_B\left(\mathrm{solid},T\right)\]

\[=\int^{T_F}_T{C_P\left(B,\mathrm{solid},T\right)}dT+{\Delta }_{\mathrm{fus}}{\overline{H}}_B\left(T_F\right)-L^o_B\left(T_F\right)+{\overline{L}}_B\left({\underline{m}}_A,T_F\right)+\int^T_{T_F}{\left[{\overline{J}}_B\left(T\right)+\mathrm{\ }C_P\left(B,\mathrm{liquid},T\right)\right]}dT\]

\[={\Delta }_{\mathrm{fus}}{\overline{H}}_B\left(T_F\right)+{\overline{L}}_B\left({\underline{m}}_A,T_F\right)-L^o_B\left(T_F\right)-\int^{T_F}_T{\left[C_P\left(B,\mathrm{liquid},T\right)-C_P\left(B,\mathrm{solid},T\right)+{\overline{J}}_B\right]}dT\]

Ya que sabemos determinar\({\overline{J}}_B\) y las capacidades de calor como funciones de temperatura, podemos evaluar esta integral para obtener una función de temperatura. Para los propósitos actuales, supongamos que\({\overline{J}}_B\) y las capacidades térmicas son esencialmente constantes e introduzcamos la abreviatura\(\Delta C_P=C_P\left(B,\mathrm{liquid},T\right)-C_P\left(B,\mathrm{solid},T\right)\), de manera que\[\int^{T_F}_T{\left[C_P\left(B,\mathrm{liquid},T\right)-C_P\left(B,\mathrm{solid},T\right)+{\overline{J}}_B\right]}dT=\left(\Delta C_P+{\overline{J}}_B\right)\left(T_F-T\right)\]

El derivado de temperatura de\({ \ln {\tilde{a}}_B\ }\left(\mathrm{solution},\ {\underline{m}}_A,T\right)\) se convierte

\[{\left(\frac{\partial { \ln {\tilde{a}}_B\ }\left(\mathrm{solution},\ {\underline{m}}_A,T\right)}{\partial T}\right)}_{P,{\underline{m}}_A}\]\[=\frac{-{\Delta }_{\mathrm{fus}}{\overline{H}}_B\left(T_F\right)-{\overline{L}}_B\left({\underline{m}}_A,T_F\right)+L^o_B\left(T_F\right)}{RT^2}+\frac{\left(\Delta C_P+{\overline{J}}_B\right)\left(T_F-T\right)}{RT^2}\]

\(T_{fp}\)es el punto de congelación de la solución cuya composición está especificada por\({\underline{m}}_A\). En\(T_{fp}\) el disolvente en esta solución está en equilibrio con disolvente sólido puro. Por lo tanto, el potencial químico del disolvente en solución es igual al del disolvente sólido puro. Entonces, debido a que el sólido puro es el estado estándar de actividad tanto para el disolvente en solución como para el disolvente sólido puro\(T_{fp}\), la actividad del disolvente en solución es igual a la del disolvente sólido puro. Debido a que el sólido puro es el estado estándar de actividad, la actividad del disolvente es la unidad en\(T_{fp}\). Esto significa que podemos integrar el derivado de temperatura de\(T_{fp}\)\(T_F\) a para obtener

\[\begin{aligned} \int^{T_F}_{T_{fp}} d ~ \ln \tilde{a}_B \left(\mathrm{solution},\ {\underline{m}}_A,T\right) & ~ \\ ~ & = \ln \tilde{a}_B \left(\mathrm{solution},\ {\underline{m}}_A,T_F\right) \\ ~ & = \left( \frac{\Delta _{\text{fus}} \overline{H}_B \left(T_F \right)+ \overline{L}_B \left( \underline{m}_A, T_F \right) +L^o_B\left(T_F\right)}{R} \right) \left(\frac{1}{T_F}-\frac{1}{T_{fp}}\right) -\left(\frac{\Delta C_P+ \overline{J}_B}{R}\right) \left(1-\frac{T_F}{T_{fp}}+ \ln \left(\frac{T_F}{T_{fp}} \right) \right) \end{aligned}\]

Así, a partir del punto de congelación medido de una solución cuya composición se especifica por\({\underline{m}}_A\), podemos calcular la actividad del disolvente en esa solución en\(T_F\).

Varias características de este resultado merecen mención. Es importante recordar que lo obtuvimos asumiendo que\(\Delta C_P+{\overline{J}}_B\left(T\right)\) es una constante. Esto suele ser una buena suposición. Se acostumbra expresar los resultados experimentales como valores de la depresión del punto de congelación,\(\Delta T=T_F-T_{fp}\). La ecuación de la actividad se convierte

\[\begin{aligned} \ln \tilde{a}_B \left(\mathrm{solution}, \underline{m}_A,T_F\right) & ~ \\ ~ & =-\left(\frac{\Delta _{\mathrm{fus}} \overline{H}_B\left(T_F\right)+\overline{L}_B\left( \underline{m}_A,T_F\right)+L^o_B\left(T_F\right)}{RT_FT_{fp}}\right)\Delta T \\ ~ & +\left(\frac{\Delta C_P+{\overline{J}}_B}{R}\right)\left(\frac{\Delta T}{T_{fp}}-{ \ln \left(1+\frac{\Delta T}{T_{fp}}\right)\ }\right) \end{aligned}\]

Los términos que involucran\({\overline{L}}_B\),\(L^o_B\),\(\Delta C_P\), y a menudo\({\overline{J}}_B\) son insignificantes, particularmente cuando la concentración de soluto es baja. Cuando\({T_F}/{T_{fp}\approx 1}\), es decir, cuando la depresión del punto de congelación es pequeña, el coeficiente de\(\Delta C_P+{\overline{J}}_B\) es aproximadamente cero. Cuando se aplican estas aproximaciones, la ecuación de actividad se aproxima por

\[{ \ln {\tilde{a}}_B\ }\left(\mathrm{solution},\ {\underline{m}}_A,T_F\right)=-\left(\frac{{\Delta }_{\mathrm{fus}}{\overline{H}}_B\left(T_F\right)}{RT^2_F}\right)\Delta T\]