20.1: La aproximación de moléculas independientes

En el Capítulo 18, nuestro estudio de la mecánica cuántica introduce la idea de que una molécula puede tener cualquiera de un número infinito de energías discretas, que podemos poner en orden comenzando por las más pequeñas. Ahora volvemos nuestra atención a las propiedades de un sistema compuesto por un gran número de moléculas. Este sistema multi-molécula debe obedecer las leyes de la mecánica cuántica. Por lo tanto, existe una ecuación de Schrödinger, cuyas variables incluyen todos los términos de distancia internúcleo, interelectrón y electrón-núcleo y potencial en todo el sistema multimolecular. Las condiciones de límite relevantes se aplican en los límites físicos del sistema macroscópico. Las soluciones de esta ecuación incluyen un conjunto de infinitamente muchas funciones de onda\({\mathit{\Psi}}_{i,j}\), cada una de las cuales describe un estado mecánico cuántico de todo el sistema multi-molécula. En general, la colección de partículas elementales que se pueden ensamblar en un sistema de múltiples moléculas en particular también se puede ensamblar en muchos otros sistemas de múltiples moléculas. Por ejemplo, una mezcla equimolar de\(CO\) y se\(H_2O\) puede volver a montar en un sistema compuesto por equimolar\(CO_2\) y\(H_2\), o en muchos otros sistemas que contienen mezclas de\(CO\),\(H_2O\),\(CO_2\), y\(H_2\). Infinitamente muchos estados cuántico-mecánicos están disponibles para cada uno de estos sistemas de múltiples moléculas.

Por cada tal función de onda multi-molécula,\({\psi }_{i,j}\), hay una energía del sistema correspondiente,\(E_i\). En general, la energía del sistema\(E_i\),, es\({\mathit{\Omega}}_i\) -fold degenerada; hay\({\mathit{\Omega}}_i\) ondulaciones,,\({\mathit{\Psi}}_{i,1}\)\({\mathit{\Psi}}_{i,2}\),...,\({\mathit{\Psi}}_{i,{\mathit{\Omega}}_i}\), cuya energía es\(E_i\). Las funciones de onda incluyen todas las interacciones entre las moléculas del sistema, y los niveles de energía del sistema reflejan todas estas interacciones. Si bien generar y resolver esta ecuación de Schrödinger multimolécula es sencilla en principio, es completamente imposible en la práctica.

Afortunadamente, podemos modelar sistemas multi-moléculas de otra manera. El enfoque principal de la química es el estudio de las propiedades y reacciones de las moléculas. En efecto, la ciencia de la química existe, tal como la conocemos, sólo porque los átomos que comprenden una molécula se pegan entre sí más tenazmente que las moléculas se adhieren entre sí. (Donde esto no es cierto, obtenemos materiales macromoleculares como metales, sales cristalinas, etc.) Esto ocurre porque las energías que caracterizan las interacciones de los átomos dentro de una molécula son mucho mayores que las energías que caracterizan la interacción de una molécula con otra. En consecuencia, la energía del sistema puede verse como la suma de dos términos. Un término es una suma de las energías que tendrían las moléculas componentes si todas estuvieran infinitamente separadas. El otro término es una suma de las energías de todas las interacciones intermoleculares, que es el cambio energético que se produciría si las moléculas fueran traídas de un estado de separación infinita al estado de interés.

En principio, podemos describir un sistema multi-molécula de esta manera con total precisión. Esta descripción tiene la ventaja de que rompe un problema muy grande y complejo en dos problemas menores, uno de los cuales ya hemos resuelto: En el Capítulo 18, vemos que podemos aproximar la descripción cuántico-mecánica de una molécula y sus niveles de energía factorizando los movimientos moleculares en componentes traslacionales, rotacionales, vibracionales y electrónicos. Solo queda describir las interacciones intermoleculares. Cuando las energías intramoleculares son mucho mayores que las energías de interacción intermolecular, puede ser una buena aproximación ignorar las interacciones intermoleculares por completo. Esto ocurre cuando describimos moléculas de gas ideales; en el límite en que un gas se comporta idealmente, la fuerza entre dos de sus moléculas es nula.

En el Capítulo 23, volvemos a la idea de las funciones de onda multi-molécula y los niveles de energía. En tanto asumimos que las interacciones intermoleculares pueden ser ignoradas. Esta es una mala aproximación para muchos sistemas. Sin embargo, es una buena aproximación para muchos otros, y nos permite mantener nuestra descripción del sistema simple mientras utilizamos propiedades moleculares en nuestro desarrollo de las ideas esenciales de la termodinámica estadística.

Nos enfocamos en desarrollar una teoría que dé las propiedades termodinámicas macroscópicas de una sustancia pura en términos de los niveles de energía disponibles para sus moléculas individuales. Para comenzar, suponemos que resolvemos la ecuación de Schrödinger para una molécula aislada. En esta ecuación de Schrödinger, las variables incluyen la distancia entre núcleos, interelectrones y electrón-núcleo y términos potenciales que son necesarios para describir la molécula. Las soluciones son un conjunto de infinitamente muchas funciones de onda\({\psi }_{i,j}\), cada una de las cuales describe un estado cuántico-mecánico diferente de una molécula aislada. Nos referimos a cada una de las posibles funciones de onda como estado cuántico de la molécula. Para cada función de onda, hay una energía molecular correspondiente,\({\epsilon }_i\). Cada energía molecular única,\({\epsilon }_i\), se llama nivel de energía. Varios estados cuánticos pueden tener la misma energía. Cuando dos o más estados cuánticos tienen la misma energía, decimos que pertenecen al mismo nivel de energía, y se dice que el nivel de energía es degenerado. En general, hay estados\(g_i\) cuánticos que podemos representar por las\(g_i\) ondulaciones,,,\({\psi }_{i,1}\),...\({\psi }_{i,2}\),,,\({\psi }_{i,g_i}\), cada una de cuya energía es\({\epsilon }_i\). Al número de estados cuánticos que tienen la misma energía se le llama degeneración del nivel energético. La Figura 1 ilustra los términos que utilizamos para describir los estados cuánticos y los niveles de energía disponibles para una molécula.

Figura 1. Estados cuánticos y niveles de energía degenerada.

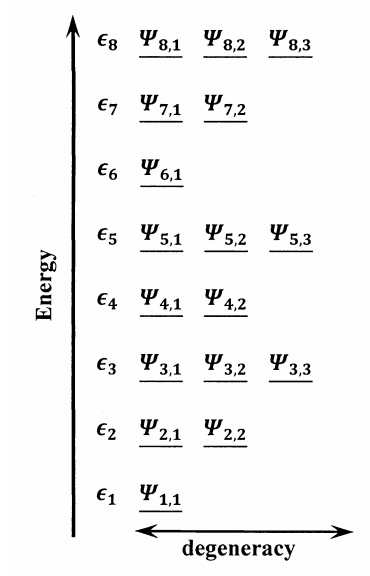
En nuestro desarrollo de la termodinámica clásica, nos parece conveniente expresar el valor de una propiedad termodinámica de una sustancia pura como el cambio que ocurre durante un proceso formal que forma un mol de la sustancia, en su estado estándar, a partir de sus elementos constitutivos no mezclados, en sus estados estándar. Al desarrollar la termodinámica estadística, nos parece conveniente expresar el valor de una energía molecular\({\epsilon }_i\), como el cambio que se produce durante un proceso formal que forma una molécula de la sustancia, en uno de sus estados cuánticos,\({\psi }_{i,j}\), a partir de sus átomos constituyentes infinitamente separados, estacionarios . Es decir, dejamos que los átomos constitutivos aislados sean el estado de referencia para las propiedades termodinámicas de una sustancia pura.