24.7: La función de partición electrónica de un gas ideal

Nuestro modelo cuántico-mecánico para una molécula diatómica toma el cero de energía para ser los átomos infinitamente separados en reposo, es decir, sin energía cinética. Las interacciones eléctricas entre los núcleos y electrones son tales que, a medida que los átomos se acercan entre sí, se forma un enlace y la energía del sistema de dos átomos disminuye. A cierta distancia internuclear, la energía alcanza un mínimo; a distancias internucleares más cortas, las interacciones repulsivas entre los núcleos comienzan a dominar, y la energía aumenta. Podemos usar la mecánica cuántica para encontrar la función de onda y la energía de la molécula cuando los núcleos están separados a cualquier distancia fija. Al repetir el cálculo a una serie de distancias internucleares, podemos encontrar la distancia a la que la energía molecular es mínima. Tomamos esta energía mínima como la energía electrónica de la molécula, y la distancia internuclear correspondiente como la longitud del enlace. Esta es la energía del estado electrónico más bajo de la molécula. El estado electrónico más bajo se llama estado básico.

Existen estados electrónicos excitados, y sus energías pueden estimarse a partir de mediciones espectroscópicas o mediante cálculo mecánico cuántico. Para la mayoría de las moléculas, estos estados electrónicos excitados tienen una energía mucho mayor que el estado básico. Cuando comparamos los términos en la función de partición electrónica, vemos que

\[{\mathrm{exp} \left({-{\epsilon }_{e,1}}/{kT}\right)\ }\gg {\mathrm{exp} \left({-{\epsilon }_{e,2}}/{kT}\right)\ }\]

El término para cualquier nivel de energía superior es insignificante en comparación con el término para el estado base. La función de partición electrónica se convierte en

\[z_e=g_1{\mathrm{exp} \left({-{\epsilon }_{e,1}}/{kT}\right)\ }\]

La degeneración del estado del suelo,\(g_1\), es una para la mayoría de las moléculas. Para las moléculas inusuales, la degeneración del estado básico puede ser mayor; para las moléculas con un electrón desapareado, es dos.

La energía del estado básico electrónico que obtenemos por cálculo mecánico cuántico directo incluye los efectos energéticos de los movimientos de los electrones y los efectos energéticos de las interacciones eléctricas entre los electrones y los núcleos estacionarios. Debido a que la calculamos para núcleos estacionarios, la energía electrónica no incluye la energía de los movimientos nucleares. La energía electrónica del estado básico es la energía liberada cuando los átomos se unen desde la separación infinita a un estado en el que están en reposo en la separación internuclear de equilibrio. Esto es solo menos una vez el trabajo requerido para separar los átomos a una distancia infinita, a partir de la separación internuclear con la energía más pequeña. En una gráfica de energía electrónica (o potencial) versus distancia internuclear, la energía del estado básico es solo la profundidad de la energía bien medida de arriba hacia abajo\(\left({\epsilon }_{e,1}<0\right)\). El trabajo requerido para separar un mol de estas moléculas en sus átomos constituyentes se denomina energía de disociación en equilibrio, y convencionalmente se le da el símbolo\(D_e\). Estas definiciones significan que\(D_e>0\) y\(D_e=-\overline{N}{\epsilon }_{e,1}\).

Figura 1. Energía de disociación de equilibrio\(D_e\),, y energía de disociación espectroscópica,\(D_0\).

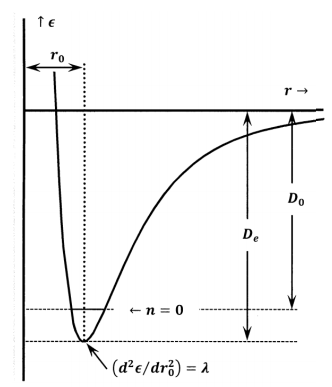
En la práctica, la energía del estado básico electrónico a menudo se estima a partir de mediciones espectroscópicas. Mediante un estudio cuidadoso de sus espectros, es posible averiguar cuánta energía se debe agregar, como fotón, para hacer que una molécula se disocie en átomos. Expresada por mol, esta energía se llama la energía de disociación espectroscópica, y convencionalmente se le da el símbolo\(D_0\). Estas mediciones espectroscópicas implican la absorción de fotones por moléculas reales. Antes de que absorban el fotón, estas moléculas ya tienen energía en forma de movimientos vibracionales y rotacionales. Entonces las moléculas reales que están involucradas en cualquier medición espectroscópica tienen energías que son mayores que las energías de las hipotéticas moléculas inmóviles de átomos en el fondo del pozo de energía potencial. Esto significa que se requiere menos energía para separar la molécula real que la que se requiere para separar la molécula hipotética en el fondo del pozo. Para cualquier molécula,\(D_e\mathrm{>}D_0\).

Para tener la menor energía posible, una molécula real debe estar en sus niveles de energía rotacional más bajos y vibracionales más bajos. Resulta que una molécula puede tener cero energía rotacional, pero su energía vibratoria nunca puede ser cero. En la Sección 24.8 revisamos la aproximación del oscilador armónico. En su nivel de energía vibracional más bajo\(\left(n=0\right)\), la energía vibratoria mínima de una molécula diatómica es\({h\nu }/{\mathrm{2}}\). \(D_0\)y\(\nu\) puede estimarse a partir de experimentos espectroscópicos. Estimamos

\[{\epsilon }_{e,1}=-\frac{D_e}{\overline{N}}=-\left(\frac{D_0}{\overline{N}}+\frac{h\nu }{2}\right)\]

y la función de partición electrónica molecular se convierte en

\[z_e=g_1{\mathrm{exp} \left(\frac{D_0}{\overline{N}kT}+\frac{h\nu }{2kT}\right)\ }\]

o

\[z_e=g_1{\mathrm{exp} \left(\frac{D_0}{RT}+\frac{h\nu }{2kT}\right)\ }\]