8.3: Consideraciones de simetría

El campo potencial de un núcleo en un átomo es esféricamente simétrico, dependiendo únicamente de la distancia entre el núcleo y el electrón. En consecuencia, las simetrías espaciales de los orbitales atómicos están completamente determinadas por los números cuánticos de momento angular l y m. Cuando se utilizan coordenadas polares esféricas en lugar de coordenadas cartesianas para describir los orbitales (Fig. 8-3), la dependencia de los orbitales de los ángulos q y f se determina por sus números cuánticos de momento angular.

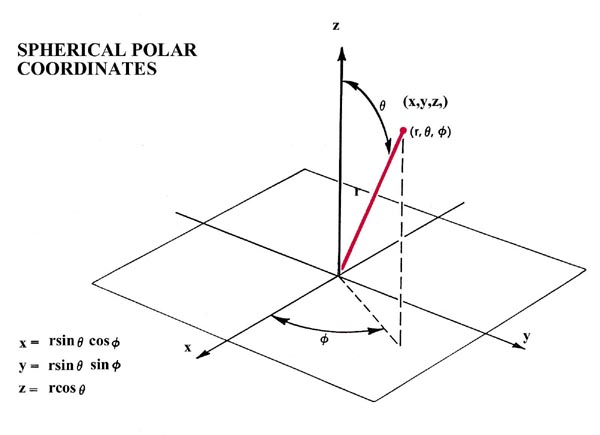
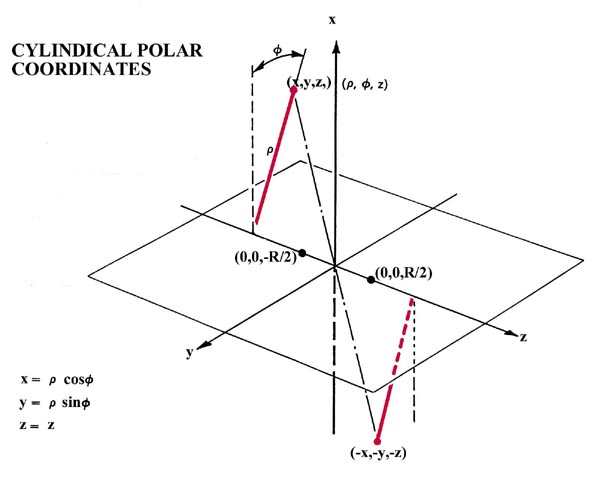
Fig. 8-3. Las relaciones de los sistemas de coordenadas polares esféricos y polares cilíndricos con los ejes cartesianos x, y y z. La operación de inversión transforma el punto (x, y, z) en el punto (-x, -y, -z).

Sólo la dependencia radial (la dependencia del orbital de la coordenada r, la distancia entre el núcleo y el electrón) difiere entre orbitales con los mismos valores l y m pero diferentes valores de n.

El campo potencial de los núcleos en una molécula lineal posee simetría cilíndrica. En términos de un sistema de coordenadas cilíndricas (Fig. 8-3) el número cuántico de momento angular único l determina la dependencia de los orbitales moleculares del ángulo f, una dependencia que determina la simetría del orbital para una rotación alrededor del eje internuclear. La dependencia de los orbitales moleculares de r y z queda indeterminada.

Las formas de los orbitales no están tan completamente determinadas por los números cuánticos de momento angular en una molécula como en un átomo. Sin embargo, podemos caracterizar y etiquetar los orbitales para un sistema molecular aprovechando la simetría que posee la molécula. La simetría del campo potencial en el que se mueve un electrón impone restricciones muy severas a las posibles formas de los orbitales. Este es un resultado muy general y poderoso. De hecho, la dependencia angular de los orbitales y las funciones de onda y sus números cuánticos de momento angular pueden estar completamente determinados únicamente por una consideración de la simetría rotacional de un sistema.

Podemos ilustrar el papel que juega la simetría en la determinación de la forma de un orbital considerando las propiedades de simetría de los orbitales obtenidos en la Sección 2 para el caso de un electrón confinado para moverse en una línea de longitud fija. Cambiemos el origen del eje x en las gráficas de los orbitales (Fig. 2-8) al punto medio de la línea, cambiando así los valores de las coordenadas de los dos puntos finales de 0 y L a - L /2 y + L /2 respectivamente. A continuación denotemos con el símbolo R la operación de reflexión a través del origen, una operación que reemplaza cada valor de x por - x. Por ejemplo, los puntos finales x = - L /2 y x = + L /2 son intercambiados por el operador de reflexión R.

El primer punto a tener en cuenta sobre la operación de reflexión es que su aplicación deja inalterado al propio sistema físico. Se supone que el potencial en el que se mueve el electrón es de valor constante a lo largo del eje x. El operador de reflexión simplemente intercambia las dos mitades de la línea dejando el sistema sin cambios. Se dice que el potencial es invariante a la operación de reflexión a través del origen.

¿Cuál es el efecto de R en las funciones de onda u orbitales? Cuando R opera sobre y ₁ (x) (es decir, cuando y ₁ (x) se refleja a través del origen) el resultado es obviamente cambiar y ₁ (x) en sí mismo:

\[\hat{R} | \psi_2(x) \rangle = \psi_2(-1x) \rangle = (+1) | \psi_2 (x) \rangle\]

La función reflejada y ₁ (- x) es indistinguible de y ₁ (x).

El resultado de operar en y ₁ (x) con el operador R es dejar la función sin cambios. y ₁ (x) se dice que es simétrico con respecto a una reflexión a través del origen. La operación de R en y ₂ (x) produce un resultado diferente:

\[\hat{R} | \psi_2(x) \rangle = \psi_2(-x) \rangle = (-1) | \psi_2 (x) \rangle\]

Es obvio a partir de la Fig. 2-8 que la reflexión de y ₂ (x) a través del punto medio cambia su signo, la función reflejada y ₂ (- x) es el negativo de la función no reflejada y ₂ (x). Se dice que tal función es antisimétrica con respecto a una reflexión en el origen. Cada orbital para este sistema es simétrico (aquellos con valores n impares) o antisimétrico (aquellos con valores pares n) con respecto a la operación de simetría de reflexión.

Cualquier orbital que no fuera simétrica ni antisimétrica, sino que fuera simplemente asimétrica con respecto a la reflexión, al cuadrado produciría una distribución de probabilidad asimétrica. Una distribución de probabilidad asimétrica implica que es más probable que el electrón se encuentre en una mitad del eje x que en el otro. Este es un resultado físicamente inaceptable ya que no hay fuerzas que actúen sobre el electrón que favorezcan un extremo de la línea sobre el otro. Solo los orbitales simétricos o antisimétricos producen distribuciones de densidad que reflejan adecuadamente la simetría del sistema (Fig. 2-4), es decir, distribuciones de densidad que son simétricas con respecto a la reflexión en el punto medio de la línea.

Por lo tanto, concluimos que las únicas funciones de onda que resultan en distribuciones de probabilidad físicamente aceptables son aquellas que son simétricas o antisimétricas con respecto a cualquier operación de simetría que cambie el sistema físico en sí mismo. Esta afirmación siempre es cierta para las funciones de onda no degeneradas, pero debe modificarse un poco para la acción de algunas operaciones de simetría en un conjunto degenerado de funciones de onda.

Utilizaremos solo uno de los muchos elementos de simetría que posee una molécula diatómica homonuclear para caracterizar y clasificar aún más los orbitales moleculares. Una molécula diatómica homonuclear posee un centro de simetría y el operador correspondiente se llama operador de inversión. La acción de este operador, denotada por el símbolo i, consiste en sustituir las coordenadas x, y, z de cada punto en el espacio por sus negativos - x, - y, - z. Esto corresponde a una inversión (o reflexión) de cada punto a través del origen o centro de simetría de la molécula (Fig. 8-3).

La acción del operador de inversión sobre las coordenadas nucleares simplemente intercambia un núcleo por otro. Dado que los núcleos poseen cargas idénticas, la estructura nuclear se deja sin cambios y el potencial ejercido por los núcleos es invariante a la operación de inversión. Así, cada orbital molecular para una molécula homonuclear debe ser simétrico o antisimétrico con respecto al operador de inversión. Los orbitales que se dejan inalterados por la operación de inversión (son simétricos) se etiquetan con un subíndice g, mientras que los que sufren un cambio de signo (son antisimétricos) se etiquetan con u. Los símbolos g y u provienen de las palabras alemanas “gerade” y “ungerade” que significan “par” e “impar” respectivamente.

Colaboradores y Atribuciones

• Dr. Richard F.W. Bader  (Professor of Chemistry / McMaster University)