1.5: Resolver numéricamente la ecuación de Schrödinger

A menudo, los potenciales ligados que encontramos son complejos, y la ecuación de Schrödinger independiente del tiempo necesitará ser evaluada numéricamente. Existen dos métodos numéricos comunes para resolver los valores propios y las funciones propias de un potencial. Ambos métodos requieren truncar y discretar una región del espacio que normalmente se extiende por un espacio de Hilbert dimensional infinito. El método Numerov es un método de diferencia finita que calcula la forma de la función de onda integrando paso a paso a lo largo de una cuadrícula. El método DVR hace uso de una transformación entre una base discreta finita y la cuadrícula finita que abarca la región de interés.

Figura\(\PageIndex{1}\): Selección y discretización de un espacio delimitando la región para la que se resolverá numéricamente el TISE. Un espacio de longitud\(L\) se discretiza en\(N\) puntos separados por un espaciado\(δx\) sobre el cual el potencial varía lentamente.

El Método Numerov

Una ecuación de Schrödinger unidimensional para una partícula en un potencial se puede resolver numéricamente en una cuadrícula que discretiza la variable de posición usando un método de diferencia finita. El TISE es

\[[ T + V (x) ] \psi (x) = E \psi (x) \label{128}\]

con

\[T = - \dfrac {\hbar^{2}} {2 m} \dfrac {\partial^{2}} {\partial x^{2}},\]

que podemos escribir como

\[\psi^{\prime \prime} (x) = - k^{2} (x) \psi (x) \label{129}\]

donde

\[k^{2} (x) = \dfrac {2 m} {\hbar^{2}} [ E - V (x) ].\]

Si discretizamos la variable\(x\), eligiendo un espaciado de cuadrícula\(\delta x\) sobre el cual\(V\) varía lentamente, podemos usar una diferencia finita de tres puntos para aproximarnos a la segunda derivada:

\[f _ {i}^{\prime \prime} \approx \dfrac {1} {\delta x^{2}} \left( f \left( x _ {i + 1} \right) - 2 f \left( x _ {i} \right) + f \left( x _ {i - 1} \right) \right) \label{130}\]

La ecuación discretizada de Schrödinger se puede escribir en la forma

\[\psi \left( x _ {i + 1} \right) - 2 \psi \left( x _ {i} \right) + \psi \left( x _ {i - 1} \right) = - k^{2} \left( x _ {i} \right) \psi \left( x _ {i} \right) \label{131}\]

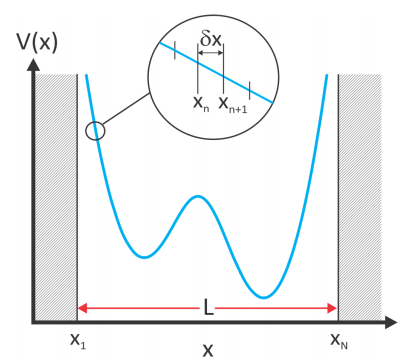
Usando la ecuación para\(\psi \left( x _ {i + 1} \right)\), uno puede resolver iterativamente para la función propia. En la práctica, se discretiza sobre un rango de espacio tal que los valores más altos y más bajos se encuentran en una región donde el potencial es muy alto o prohibido. Dividiendo el espacio en N puntos, eligió los dos primeros valores\(\psi \left( x _ {1} \right) = 0\) y\(\psi \left( x _ {2} \right)\) x para ser un pequeño número positivo o negativo\(E\), adivinar y propagar iterativamente a\(\psi \left( x _ {N} \right)\). Una comparación de las funciones de onda obtenidas al propagar de\(x_1\) a\(x_N\) con la obtenida propagándose de\(x_N\) a\(x_1\) te dice lo buena que\(E\) fue tu suposición de.

El Método Numerov mejora la Ecuación\ ref {131} al tener en cuenta la cuarta derivada de la función de onda\(\Psi^{( 4 )}\), lo que lleva a errores en el orden\(O \left( \delta x^{6} \right)\). La ecuación\ ref {130} se convierte

\[f _ {i}^{\prime \prime} \approx \dfrac {1} {\delta x^{2}} \left( f \left( x _ {i + 1} \right) - 2 f \left( x _ {i} \right) + f \left( x _ {i - 1} \right) \right) - \dfrac {\delta x^{2}} {12} f _ {i}^{( 4 )} \label{132}\]

Al diferenciar la ecuación\ ref {129} sabemos

\[\psi^{( 4 )} (x) = - \left( k^{2} (x) \psi (x) \right)^{\prime \prime}\]

y la ecuación discretizada de Schrödinger se convierte en

\[\left.\begin{aligned} \psi^{\prime \prime} \left( x _ {i} \right) & = \dfrac {1} {\delta x^{2}} \left( \psi \left( x _ {i + 1} \right) - 2 \psi \left( x _ {i} \right) + \psi \left( x _ {i - 1} \right) \right) + \\ & \dfrac {1} {12} \left( k^{2} \left( x _ {i + 1} \right) \psi \left( x _ {i + 1} \right) - 2 k^{2} \left( x _ {i + 1} \right) \psi \left( x _ {i} \right) + k^{2} \left( x _ {i + 1} \right) \psi \left( x _ {i - 1} \right) \right) \end{aligned} \right. \label{33}\]

Esta ecuación conduce a la solución iterativa para la función de onda

\[\psi \left( x _ {i + 1} \right) = \dfrac{\psi \left( x _ {i} \right) \left( 2 + \dfrac {10 \delta x^{2}} {12} k^{2} \left( x _ {i} \right) \right) - \psi \left( x _ {i - 1} \right) \left( 1 - \dfrac {\delta x^{2}} {12} k^{2} \left( x _ {i - 1} \right) \right)}{1 - \dfrac {\delta x^{2}} {12} k^{2} \left( x _ {i + 1} \right)} \label{134}\]

Representación Variable Discreta (DVR)

Las soluciones numéricas a las funciones de onda de un potencial enlazado en la representación de posición requieren truncar y discretar una región del espacio que normalmente se extiende por un espacio tridimensional infinito de Hilbert. El enfoque DVR utiliza un conjunto de bases espaciales reales cuyos autoestados\(\varphi _ {i} (x)\) conocemos y que abarcan el espacio de interés, por ejemplo, efunciones de onda de oscilador armónico, para expresar los estados propios de un hamiltoniano en una base de cuadrícula (\(\theta _ {j}\)) que pretende aproximarse a la base continua del espacio real\(\delta (x)\). Los dos conjuntos de bases, que denominamos eigenbasis (\(\varphi\)) y grid basis (\(\theta\)), se conectarán a través de una transformación unitaria

\(\Phi^{\dagger} \varphi (x) = \theta (x) \label{135}\)\(\Phi \theta (x) = \varphi (x)\)

Para los puntos\(N\) discretos en la base de la cuadrícula, habrá\(N\) vectores propios en la base propia, permitiendo que las propiedades de proyección y completitud se mantengan en ambas bases. Las funciones de onda se pueden obtener construyendo lo hamiltoniano en la propia base,

\(H = T ( \hat {p} ) + V ( \hat {x} ),\)transformándose a la base del DVR,\(H^{D V R} = \Phi H \Phi,\) y luego diagonalizando.

Aquí discutiremos una versión de DVR en la que se configura la base de la grilla para reflejar la\(| \mathcal {X} \rangle\) autobase continua. Comenzamos por elegir el rango de\(x\) que contienen los estados de interés encuadernados y discretizándolos en\(N\) puntos (\(x_i\)) igualmente espaciados por\(δx\). Suponemos que las funciones de base DVR\(\theta _ {j} \left( x _ {i} \right)\) se asemejan a la base de posición dimensional infinita

\[\theta _ {j} \left( x _ {i} \right) = \sqrt {\Delta x} \delta _ {i j} \label{136}\]

Nuestro truncamiento se habilita utilizando un operador de proyección en el espacio reducido

\[P _ {N} = \sum _ {i = 1}^{N} | \theta _ {i} \rangle \langle \theta _ {i} | \approx 1 \label{137}\]

que es válido para apropiadamente alto\(N\). El hamiltoniano completo se puede expresar en el DVR base DVR

\[H^{D V R} = T^{D V R} + V^{D V R}.\]

Para la energía potencial, ya que\(\left\{\theta _ {i} \right\}\) se localiza con\(\left\langle \theta _ {i} | \theta _ {j} \right\rangle = \delta _ {i j}\), hacemos la aproximación DVR, la cual arroja\(V^{DVR}\) en una forma diagonal que es igual a la energía potencial evaluada en el punto de la cuadrícula:

\[V _ {i j}^{D V R} = \left\langle \theta _ {i} | V ( \hat {x} ) | \theta _ {j} \right\rangle \approx V \left( x _ {i} \right) \delta _ {i j} \label{138}\]

Esto viene de aproximar la transformación como\(\Phi V ( \hat {x} ) \Phi^{\dagger} \approx V \left( \Phi \hat {x} \Phi^{\dagger} \right) . \)

Para los elementos de la matriz de energía cinética\(\left\langle \theta _ {i} | T ( \hat {p} ) | \theta _ {j} \right\rangle\), necesitamos evaluar segundas derivadas entre diferentes puntos de cuadrícula. Afortunadamente, Colbert y Miller han simplificado este proceso al encontrar una forma analítica para la\(T^{DVR}\) matriz para una caja uniformemente cuadriculada con un espaciado de cuadrícula de\(∆x\).

\[T _ {i j}^{\mathrm {DVR}} = \dfrac {\hbar^{2} ( - 1 )^{i - j}} {2 m \Delta x^{2}} \left\{\begin{array} {c c} {\pi^{2} / 3} & {i = j} \\ {2 / ( i - j )^{2}} & {i \neq j} \end{array} \right\} \label{139}\]

Esto proviene de una expansión de Fourier en una caja uniformemente cuadriculada. Naturalmente, esto parece oscilatorio\(x\) en el período de\(δx\). La expresión se vuelve exacta en el límite de\(N \rightarrow \infty\) o\(\Delta x \rightarrow 0\). La rutina numérica se vuelve simple y eficiente. Construimos un relleno hamiltoniano con elementos de matriz cuyas contribuciones potenciales y de energía cinética están dadas por las Ecuaciones\ ref {138} y\ ref {139}. Después diagonalizamos\(H^{DVR}\), a partir de lo cual obtenemos\(N\) valores propios y las\(N\) correspondientes funciones propias.

Referencias

1. I. N. Levine, Química Cuántica, 5ta ed. (Prentice Hall, Englewood Cliffs, NJ, 2000).
2. J. C. Light y T. Carrington, “Representaciones discreto-variables y su utilización” en Avances en Física Química (John Wiley & Sons, Inc., 2007), pp. 263-310;
3. D. J. Tannor, Introducción a la mecánica cuántica: una perspectiva dependiente del tiempo. (Libros de Ciencias Universitarias, Sausilito, CA, 2007).
4. D. T. Colbert y W. H. Miller, Una nueva representación variable discreta para dispersión reactiva mecánica cuántica a través del método Kohn de matriz S, J. Chem. Phys. 96, 1982-1991 (1992).