1.4: Operadores exponenciales

A lo largo de nuestro trabajo, haremos uso de operadores exponenciales de la forma

\[\hat {T} = e^{- i \hat {A}} \label{115}\]

Veremos que estos operadores exponenciales actúan sobre una función de onda para moverla en el tiempo y el espacio, y por lo tanto también se les conoce como propagadores. De particular interés para nosotros es el operador de evolución temporal,\(\hat {U} = e^{- i \hat {H} t / \hbar},\) que propaga la función de onda en el tiempo. Tenga en cuenta que el operador\(\hat{T}\) es una función de un operador,\(f(\hat{A})\). Una función de un operador se define a través de su expansión en una serie Taylor, por ejemplo

\[\hat {T} = e^{- \hat {i} \hat {A}} = \sum _ {n = 0}^{\infty} \dfrac {( - i \hat {A} )^{n}} {n !} = 1 - i \hat {\hat {A}} - \dfrac {\hat {A} \hat {A}} {2} - \cdots \label{116}\]

Dado que los usamos con tanta frecuencia, revisemos las propiedades de los operadores exponenciales que se pueden establecer con la ecuación\ ref {116}. Si el operador\(\hat {A}\) es hermitiano, entonces\(\hat {T} = e^{- i \hat {A}}\) es unitario, es decir,\(\hat {T}^{\dagger} = \hat {T}^{- 1}.\) Así el conjugado hermitiano de\(\hat {T}\) invierte la acción de\(\hat {T}\). Para el propagador de tiempo\(\vec {U}\), a menudo\(\vec {U}^{\dagger}\) se conoce como el operador de inversión de tiempo.

Los estados propios del operador\(\hat {A}\) también son estados propios de\(f(\hat {A})\), y los valores propios son funciones de los valores propios de\(\hat {A}\). A saber, si conoces los valores propios y los vectores propios de\(\hat {A}\), es decir,\(\hat {A} \varphi _ {n} = a _ {n} \varphi _ {n},\) puedes mostrar expandiendo la función

\[f ( \hat {A} ) \varphi _ {n} = f \left( a _ {n} \right) \varphi _ {n} \label{117}\]

Nuestra aplicación más común de esta propiedad será a operadores exponenciales que involucren a los hamiltonianos. Dados los autoestados\(\varphi _ {n}\), entonces\(\hat {H} | \varphi _ {n} \rangle = E _ {n} | \varphi _ {n} \rangle\) implica

\[e^{- i \hat {H} t / \hbar} | \varphi _ {n} \rangle = e^{- i E _ {n} t / \hbar} | \varphi _ {n} \rangle \label{118}\]

Así como lo\(\hat {D} _ {x} ( \lambda )\) es el operador de evolución temporal que desplaza la función de onda en el tiempo,\(\hat {D} _ {x} = e^{- i \hat {p} _ {x} x / h}\) es el operador de desplazamiento espacial que se mueve\(\psi\) a lo largo de la\(x\) coordenada. Si definimos\(\hat {D}_ {x} = e^{- i \hat {p} _ {x} x / h},\) entonces la acción de es desplazar la ondafunción por una cantidad\(\lambda\)

\[| \psi ( x - \lambda ) \rangle = \hat {D} _ {x} ( \lambda ) | \psi (x) \rangle \label{119}\]

Además, aplicar\(\hat {D} _ {x} ( \lambda )\) a un operador de posición cambia al operador por\(\lambda\)

\[\hat {D} _ {x}^{\dagger} \hat {x} \hat {D} _ {x} = x + \lambda \label{120}\]

Así\(e^{- i \hat {p} _ {x} \lambda / \hbar} | x \rangle\) es un vector propio de\(\hat {x}\) con valor propio\(x + \lambda\) en lugar de\(x\). El operador

\(\hat {D} _ {x} = e^{- i \hat {p} _ {x} \lambda / h}\)es un operador de desplazamiento para coordenadas de\(x\) posición. De igual manera,\(\hat {D} _ {y} = e^{- i \hat {p} _ {y} \lambda / h}\) genera desplazamientos en\(y\) y\(\hat {D_z}\) en\(z\). Similar al propagador de tiempo\(\boldsymbol {U}\), el operador de desplazamiento\(\boldsymbol {D}\) debe ser unitario, ya que la acción de\(\hat {D}^{\dagger} \hat {D}\) debe dejar el sistema sin cambios. Es decir, si\(\hat {D} _ {x}\) cambia el sistema a\(x\) de\(x_0\), luego\(\hat {D} _ {x}^{\dagger}\) cambia el sistema de\(x\) atrás a\(x_0\).

Figura\(\PageIndex{1}\)

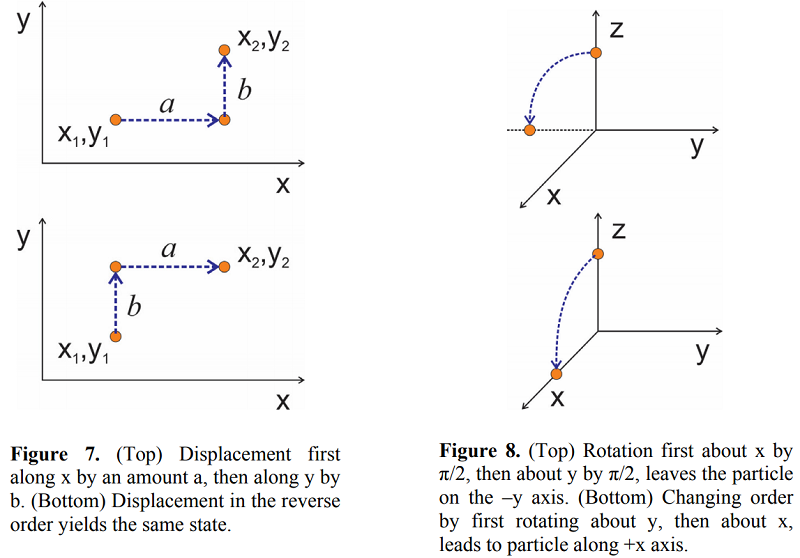
Sabemos intuitivamente que los desplazamientos lineales conmutan. Por ejemplo, si deseamos desplazar una partícula en dos dimensiones, x e y, el orden de desplazamiento no importa. Terminamos en la misma posición, ya sea que nos movemos a lo largo de x primero o a lo largo de y, como se ilustra en la Figura 7. En términos de operadores de desplazamiento, podemos escribir

\ [\ begin {alineado}
\ izquierda|x_ {2}, y_ {2}\ derecha\ rangle &=e^ {-i b p_ {y}/\ hbar} e^ {-i a p_ {x}/\ hbar}\ izquierda|x_ {1}, y_ {1}\ derecha\ rangle\\
&=e^ {-i a p_ {x}/\ hbar} e^ {-i b p_ {y}/\ hbar}\ izquierda|x_ {1}, y_ {1}\ derecha\ rangle
\ final {alineado}\]

Estos operadores de desplazamiento conmutan, como se esperaba de\([p_x,p_y] = 0.\)

Similar al operador de desplazamiento, podemos definir operadores de rotación que dependen de los operadores de momento angular\(L_x\),\(L_y\), y\(L_z\). Por ejemplo,

\[\hat {R} _ {x} ( \phi ) = e^{- i \phi L _ {x} / \hbar}\]

da una rotación por ángulo\(\phi\) alrededor del\(x\) eje. A diferencia del desplazamiento lineal, las rotaciones alrededor de diferentes ejes no se desplazan. Por ejemplo, considere un estado que representa una partícula desplazada a lo largo del eje z,\(| z 0 \rangle\). Ahora la acción de dos rotaciones\(\hat {R} _ {x}\) y\(\hat {R} _ {y}\) por un ángulo de\(\phi = \pi / 2\) sobre esta partícula difiere dependiendo del orden de operación, como se ilustra en la Figura 8. Si giramos primero sobre\(x\), la operación

\[e^{- i \tfrac {\pi} {2} L _ {y} / \hbar} e^{- i \tfrac {\pi} {2} L _ {x} / \hbar} | z _ {0} \rangle \rightarrow | - y \rangle \label{122}\]

conduce a la partícula en el eje —y, mientras que el orden inverso

\[e^{- i \tfrac {\pi} {2} L _ {x} / \hbar} e^{- i \tfrac {\pi} {2} L _ {y} / \hbar} | z _ {0} \rangle \rightarrow | + x \rangle \label{123}\]

conduce a la partícula en el eje +x. El estado final de estas dos rotaciones tomadas en orden opuesto difiere por una rotación alrededor del eje z. Dado que las rotaciones alrededor de diferentes ejes no se desplazan, esperamos que los operadores de momento angular no conmuten. En efecto, sabemos que

\[\left[ L _ {x} , L _ {y} \right] = i \hbar L _ {z}\]

donde el conmutador de rotaciones alrededor de los ejes x e y está relacionado por una rotación del eje z. Al igual que con los operadores de rotación, tendremos que tener cuidado con los propagadores de tiempo para determinar si el orden de propagación del tiempo importa. Esto, a su vez, dependerá de si los hamiltonianos en dos puntos en el tiempo conmutan.

Propiedades de los operadores exponenciales

1. Si\(\hat{A}\) y\(\hat{B}\) no conmuta, sino que se\([ \hat {A} , \hat {B} ]\) desplaza con\(\hat{A}\) y\(\hat{B}\), entonces

\[e^{\hat {A} + \hat {B}} = e^{\hat {A}} e^{\hat {B}} e^{- \frac {1} {2} [ \hat {A} , \hat {B} ]} \label{124}\]

\[e^{\hat {A}} e^{\hat {B}} = e^{\hat {B}} e^{\hat {A}} e^{- [ \hat {B} , \hat {A} ]} \label{125}\]

2. De manera más general, si\(\hat{A}\) y\(\hat{B}\) no conmutan,

\[ e^{\hat {A}} e^{\hat {B}} = {\mathrm {exp}} \left[ \hat {A} + \hat {B} + \dfrac {1} {2} [ \hat {A} , \hat {B} ] + \dfrac {1} {12} ( [ \hat {A} , [ \hat {A} , \hat {B} ] ] + [ \hat {A} , [ \hat {B} , \hat {B} ] ] ) + \cdots \right] \label{126}\]

3. La relación Baker—Hausdorff:

\[\left. \begin{array} {r l} {\mathrm {e}^{i \hat {G} \lambda} \hat {A} \mathrm {e}^{- i \hat {G} \lambda} = \hat {A} + i \lambda [ \hat {G} , \hat {A} ] + \left( \dfrac {i^{2} \lambda^{2}} {2 !} \right) [ \hat {G} , [ \hat {G} , \hat {A} ] ] + \ldots} \\ {} & {+ \left( \dfrac {i^{n} \lambda^{n}} {n !} \right) [ \hat {G} , [ \hat {G} , [ \hat {G} , \hat {A} ] ] ] \ldots ] + \ldots} \end{array} \right. \label{127}\]

donde\(λ\) es un número.