2.3: Sistemas de dos niveles

Usemos el propagador de tiempo en un cálculo de modelo al que nos referiremos a menudo. Es común reducir o mapear problemas cuánticos en un sistema de dos niveles (2LS). Escogeremos los estados más importantes para nuestro problema y encontraremos estrategias para descartar o simplificar la influencia de los restantes grados de libertad. Considere un 2LS con dos estados imperturbables o de “orden cero”\(| \varphi _ {a} \rangle\) y\(| \varphi _ {b} \rangle\) con energías\( {\varepsilon} _ {a}\) y\( {\varepsilon} _ {b}\), que son descritos por un hamiltoniano de orden cero\(H_0\):

\[\begin{align} \hat {H} _ {0} &= | \varphi _ {a} \rangle \varepsilon _ {a} \left\langle \varphi _ {a} | + | \varphi _ {b} \right\rangle \varepsilon _ {b} \langle \varphi _ {b} | \\[4pt] &= \left( \begin{array} {l l} {\varepsilon _ {a}} & {0} \\[4pt] {0} & {\varepsilon _ {b}} \end{array} \right) \label{1.33} \end{align}\]

Estos estados interactúan a través de un acoplamiento\(V\) de la forma

\[\begin{align} \hat {V} &= | \varphi _ {a} \rangle V _ {a b} \left\langle \varphi _ {b} | + | \varphi _ {b} \right\rangle V _ {b a} \langle \varphi _ {a} | \\[4pt] &= \left( \begin{array} {l l} {0} & {V _ {a b}} \\[4pt] {V _ {b a}} & {0} \end{array} \right) \label{1.34} \end{align}\]

El hamiltoniano completo para los dos estados acoplados es\(\hat{H}\):

\[\begin{align} \hat {H} & = \hat {H} _ {0} + \hat {V} \\[4pt] & = \left( \begin{array} {c c} {\varepsilon _ {a}} & {V _ {a b}} \\[4pt] {V _ {b a}} & {\varepsilon _ {b}} \end{array} \right) \label{1.35} \end{align} \]

Los estados de orden cero son\(| \varphi _ {a} \rangle\) y\(| \varphi _ {b} \rangle\). El acoplamiento mezcla estos estados, dando lugar a dos autoestados de\(\hat{H}\),\(| \varphi _ {+} \rangle\) y\(| \varphi _ {-} \rangle\), con los correspondientes valores propios de energía\( {\varepsilon} _ {+}\) y\( {\varepsilon} _ {-}\), respectivamente.

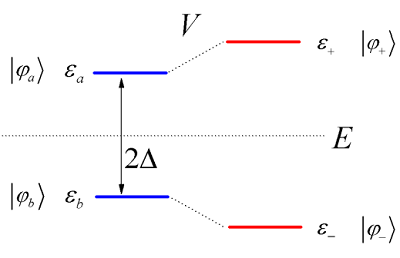
Preguntaremos: Si preparamos el sistema en estado\(| \varphi _ {a} \rangle\), ¿cuál es la probabilidad dependiente del tiempo de observarlo en\(| \varphi _ {b} \rangle\)? Dado que\(| \varphi _ {a} \rangle\) y no\(| \varphi _ {b} \rangle\) son autoestados de\(\hat{H}\), y dado que nuestra propagación en el tiempo se realizará en la base propia usando la Ecuación\ ref {1.29}, necesitaremos encontrar la transformación entre estas bases.

Comenzamos por buscar los valores propios del hamiltoniano (Ecuación\ ref {1.35}). Como el hamiltoniano es hermitiano, (\(H _ {i j} = H _ {j i}^{*}\)), escribimos

\[V _ {a b} = V _ {b a}^{*} = V e^{- i \varphi} \label{1.36}\]

\[\hat {H} = \left( \begin{array} {c c} {\varepsilon _ {a}} & {V e^{- i \varphi}} \\[4pt] {V e^{+ i \varphi}} & {\varepsilon _ {b}} \end{array} \right) \label{1.37}\]

A menudo los acoplamientos que describimos son reales, y podemos descuidar el factor de fase\(\phi\). Ahora definimos variables para la energía media y la división de energía entre los estados desacoplados

\[E = \frac {\varepsilon _ {a} + \varepsilon _ {b}} {2}\]

\[\Delta = \frac {\varepsilon _ {a} - \varepsilon _ {b}} {2} \label{1.39}\]

Entonces podemos obtener los valores propios del sistema acoplado resolviendo la ecuación secular

\[\operatorname {det} ( H - \lambda I ) = 0\]

dando

\[\varepsilon _ {\pm} = E \pm \Omega \label{1.41}\]

Aquí definí otra variable

\[\Omega = \sqrt {\Delta^{2} + V^{2}} \label{1.42}\]

Para determinar los vectores propios del sistema acoplado\(| \varphi _ {\pm} \rangle\), resulta ser una gran simplificación definir un ángulo de mezcla\(\theta\) que describa la magnitud relativa del acoplamiento en relación con la división de energía de orden cero

\[\tan 2 \theta = \frac {V} {\Delta} \label{1.43}\]

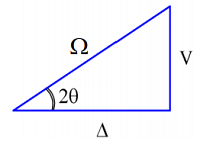
Vemos que el ángulo de mezcla adopta valores tales que\(0 \leq \theta \leq \pi / 4\). Además, observamos que

\[\sin 2 \theta = V / \Omega \label{1.44}\]

\[\cos 2 \theta = \Delta / \Omega \label{1.45}\]

En esta representación el hamiltoniano (Ecuación\ ref {1.37}) se convierte

\[\hat {H} = E \overline {I} + \Delta \left( \begin{array} {l l} {1} & {\tan 2 \theta e^{- i \varphi}} \\[4pt] {\tan 2 \theta e^{+ i \varphi}} & {- 1} \end{array} \right) \label{1.46}\]

y podemos expresar los valores propios como

\[\varepsilon _ {\pm} = E \pm \Delta \sec 2 \theta \label{1.47}\]

A continuación queremos encontrar\(S\), la transformación que diagonaliza lo hamiltoniano y que transforma los coeficientes de la función de onda de la base de orden cero a la base propia. Los estados propios se pueden expandir en la base de orden cero en la forma

\[| \varphi _ {\pm} \rangle = c _ {a} | \varphi _ {a} \rangle + c _ {b} | \varphi _ {b} \rangle \label{1.48}\]

Para que la transformación pueda expresarse en forma de matriz como

\[\left( \begin{array} {l} {\varphi _ {+}} \\[4pt] {\varphi _ {-}} \end{array} \right) = S \left( \begin{array} {l} {\varphi _ {a}} \\[4pt] {\varphi _ {b}} \end{array} \right)\label{1.49}\]

Para encontrar\(S\), usamos la ecuación de Schrödinger\(\hat {H} | \varphi _ {\pm} \rangle = \varepsilon _ {\pm} | \varphi _ {\pm} \rangle\)

sustituyendo la Ecuación\ ref {1.48}. Esto da

\[S = \left( \begin{array} {l l} {\cos \theta} & {e^{- i \varphi / 2}} & {\sin \theta} & {e^{i \varphi / 2}} \\[4pt] {- \sin \theta} & {e^{- i \varphi / 2}} & {\cos \theta} & {e^{i \varphi / 2}} \end{array} \right) \label{1.50}\]

Tenga en cuenta que\(S\) es unitario desde\(S^{\dagger} = S^{- 1}\) y\(\left( S^{T} \right)^{*} = S^{- 1}\). Además, la base propia es ortonormal:

\[\left\langle \varphi _ {+} | \varphi _ {+} \right\rangle + \left\langle \varphi _ {-} | \varphi _ {-} \right\rangle = 1.\]

Ahora, examinemos los autoestados en dos límites:

1. Acoplamiento débil (\(| {V} / \Delta | \ll 1\)). Aquí\(\theta \approx 0\), y\(| \varphi _ {+} \rangle\) corresponde a\(| \varphi _ {a} \rangle\) débilmente perturbado por la\(V_{ab}\) interacción. \(| \varphi _ {-} \rangle\)corresponde a\(| \varphi _ {b} \rangle\). De otra manera, como\(\theta \rightarrow 0\), nos encontramos\[| \varphi _ {+} \rangle \rightarrow | \varphi _ {a} \rangle\] y\[| \varphi _ {-} \rangle \rightarrow | \varphi _ {b} \rangle.\]
2. Acoplamiento fuerte (\(| V / \Delta | \gg 1\)). En este límite\(\theta = \pi / 4\), y los estados de\(a/b\) base son indistinguibles. Los autoestados son combinaciones simétricas y antisimétricas:\[| \varphi _ {\pm} \rangle = \frac {1} {\sqrt {2}} ( | \varphi _ {b} \rangle \pm | \varphi _ {a} \rangle ) \label{1.51}\] Nota de la Ecuación\ ref {1.50} que el signo de\(V\) dicta si\(| \varphi _ {+} \rangle\) o\(| \varphi _ {-} \rangle\) corresponde al autoestado simétrico o antisimétrico. Para negativo\(V \gg \Delta\),\(\theta = - \pi / 4\), y la correspondencia en la Ecuación\ ref {1.51} cambia a\(\mp\).

Podemos representar esquemáticamente las energías de estos estados con el siguiente diagrama. Aquí exploramos la gama de\( {E} _ {\pm}\) disponibles dado un acoplamiento fijo\(V\) y variando la división\(\Delta\).

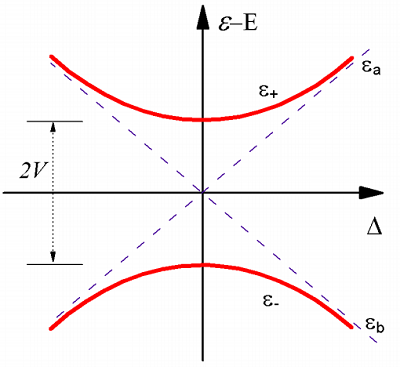
Este diagrama ilustra un efecto de cruce evitado. El fuerte límite de acoplamiento es equivalente a un punto de degeneración (\(\Delta = 0\)) entre los estados\(| \varphi _ {a} \rangle\) y\(| \varphi _ {b} \rangle\). Los estados propios mezclan completamente los estados imperturbables, pero permanecen divididos por la fuerza de la interacción\(2V\). Volveremos a la discusión de los cruces evitados cuando describamos las superficies de energía potencial y la aproximación adiabática, donde se\(R\) debe considerar la dependencia de\(V\) y\(\Delta\) de la posición.

Ahora podemos pasar a describir dinámicas. La evolución temporal de este sistema viene dada por el propagador del tiempo

\[U (t) = | \varphi _ {+} \rangle e^{- i \omega , t} \left\langle \varphi _ {+} | + | \varphi _ {-} \right\rangle e^{- i \omega t} \langle \varphi _ {-} | \label{1.52}\]

donde\(\omega _ {\pm} = \varepsilon _ {\pm} / \hbar\). Ya que\(\varphi _ {a}\) y no\(\varphi _ {b}\) son los autoestados, ¡preparar el sistema en estado\(\varphi _ {a}\) conducirá a la evolución del tiempo! Preparemos el sistema para que esté inicialmente en\(\varphi _ {a}\).

\[| \psi ( 0 ) \rangle = | \varphi _ {a} \rangle \label{1.53} \nonumber\]

Evaluando las amplitudes dependientes del tiempo de los estados inicial y final con la ayuda de\(S\), encontramos

\[\begin{align*} c _ {a} (t) & = \left\langle \varphi _ {a} | U (t) | \varphi _ {a} \right\rangle \\[4pt] & = e^{- i E t} \left[ \cos^{2} \theta e^{i \Omega _ {R} t} + \sin^{2} \theta e^{- i \Omega _ {R} t} \right] \label{1.54} \\[4pt] c _ {b} (t) & = \left\langle \varphi _ {b} | U (t) | \varphi _ {a} \right\rangle \\[4pt] & = 2 \sin \theta \cos \theta e^{- i E t} \sin \Omega _ {R} t \label{1.55} \end{align*}\]

Entonces, ¿cuál es la probabilidad de que se encuentre en estado\(| \varphi _ {b} \rangle\) a la vez\(t\)?

\[\begin{aligned} P _ {b a} (t) & = \left| c _ {b} (t) \right|^{2} \\[4pt] & = \frac {V^{2}} {V^{2} + \Delta^{2}} \sin^{2} \Omega _ {R} t \end{aligned} \label{1.56}\]

donde

\[\Omega _ {R} = \frac {1} {\hbar} \sqrt {\Delta^{2} + V^{2}} \label{1.57}\]

\(\Omega _ {R}\), la Frecuencia Rabi, representa la frecuencia a la que la amplitud de probabilidad oscila entre\(\varphi _ {a}\) y\(\varphi _ {b}\) estados.

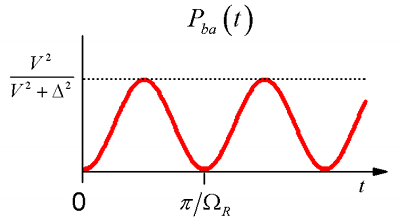
Aviso para el límite de acoplamiento débil (\(V \rightarrow 0\)),\(\varphi _ {\pm} \rightarrow \varphi _ {a , b}\) (los estados propios se asemejan a los estados estacionarios), y la dependencia del tiempo desaparece. En el límite de acoplamiento fuerte (\(V \gg \Delta\)), la amplitud se intercambia completamente entre los estados de orden cero a una velocidad dada por el acoplamiento:\(\Omega _ {R} \rightarrow V / \hbar\). Incluso en este límite toma una cantidad finita de tiempo para que la amplitud se mueva entre estados. Para obtener\(P=1\) requiere un tiempo\(\tau\):

\[\tau = \pi / 2 \Omega _ {R} = \hbar \pi / 2 V. \nonumber\]

Lecturas

1. Cohen-Tannoudji, C.; Diu, B.; Lalöe, F., Mecánica Cuántica. Wiley-Interscience: París, 1977; pp. 405-420.
2. Liboff, R. L., Introducción a la Mecánica Cuántica. Addison-Wesley: Reading, MA, 1980; p. 77.
3. Mukamel, S., Principios de Espectroscopia Óptica No Lineal. Oxford University Press: Nueva York, 1995; Ch. 2.
4. Sakurai, J. J., Mecánica Cuántica Moderna, Edición Revisada. Addison-Wesley: Reading, MA, 1994.