3.1: Operador de Evolución en el Tiempo

Empecemos por el inicio obteniendo la ecuación de movimiento que describe la función de onda y su evolución temporal a través del propagador del tiempo. Estamos buscando ecuaciones de movimiento para sistemas cuánticos que sean equivalentes a las ecuaciones de Newton, o más exactamente de Hamilton, para sistemas clásicos. La pregunta es, si conocemos la función de onda en el momento\(| \psi (\vec{r}, t_o ) \rangle \), ¿cómo cambia con el tiempo? ¿Cómo determinamos\(| \psi (\vec{r}, t ) \rangle \), para algún tiempo posterior\( t > t_o\)? Aquí utilizaremos nuestra intuición, basada en gran parte en la correspondencia con la mecánica clásica. Para mantener la notación al mínimo, en la siguiente discusión no mostraremos explícitamente la dependencia espacial de la función de onda.

Comenzamos asumiendo la causalidad:\(| \psi ( t_o ) \rangle \) precede y determina\(| \psi (t) \rangle \), lo cual es crucial para derivar una ecuación determinista del movimiento. Además, como es habitual, suponemos que el tiempo es una variable continua:

\[\lim _ {t \rightarrow \tau _ {0}} | \psi (t) \rangle = | \psi \left( t _ {0} \right) \rangle \label{2.1}\]

Ahora defina un “operador de desplazamiento temporal” o “propagador” que actúe sobre la función de onda hacia la derecha y de ese modo propague el sistema hacia adelante en el tiempo:

\[| \psi (t) \rangle = U \left( t , t _ {0} \right) | \psi \left( t _ {0} \right) \rangle \label{2.2}\]

También sabemos que el operador\(U\) no puede depender del estado del sistema\(| \psi (t) \rangle \). Esto es necesario para la conservación de la probabilidad, es decir, para retener la normalización para el sistema. Si

\[| \psi \left( t _ {0} \right) \rangle = a _ {1} | \varphi _ {1} \left( t _ {0} \right) \rangle + a _ {2} | \varphi _ {2} \left( t _ {0} \right) \rangle \label{2.3}\]

entonces

\[\begin{align} | \psi (t) \rangle & = U \left( t , t _ {0} \right) | \psi \left( t _ {0} \right) \rangle \\[4pt] & = U \left( t , t _ {0} \right) a _ {1} | \varphi _ {1} \left( t _ {0} \right) \rangle + U \left( t , t _ {0} \right) a _ {2} | \varphi _ {2} \left( t _ {0} \right) \rangle \\[4pt] & = a _ {1} (t) | \varphi _ {1} \rangle + a _ {2} (t) | \varphi _ {2} \rangle \end{align}. \label{2.4}\]

Esto es un reflejo de la importancia de la linealidad y el principio de superposición en los sistemas mecánicos cuánticos. Si bien\(|a_i(t)|\) normalmente no es igual a\(|a_i(0)|\)

\[\sum _ {n} \left| a _ {n} (t) \right|^{2} = \sum _ {n} \left| a _ {n} \left( t _ {0} \right) \right|^{2} \label{2.5}\]

Esto dicta que la ecuación diferencial de movimiento sea lineal en el tiempo.

Inmuebles de U

Ahora hacemos algunas observaciones importantes y útiles respecto a las propiedades de\(U\).

1. Unitario. Tenga en cuenta que para que la Ecuación\ ref {2.5} se mantenga y para que la densidad de probabilidad se conserve,\(U\) debe ser unitaria\[P = \langle \psi (t) | \psi (t) \rangle = \left\langle \psi \left( t _ {0} \right) \left| U^{\dagger} U \right| \psi \left( t _ {0} \right) \right\rangle \label{2.6}\] que sostiene si\(U^{\dagger} = U^{- 1}\).
2. Continuidad temporal: El estado no cambia cuando los puntos de tiempo inicial y final son los mismos\[U ( t , t ) = 1 \label{2.7}\]
3. Propiedad de composición. Si tomamos el sistema para ser determinista, entonces es lógico pensar que debemos obtener la misma función de onda tanto si evolucionamos a un tiempo objetivo en un paso (\(t_0 \rightarrow t_2\)) o múltiples pasos (\(t_0 \rightarrow t_1 \rightarrow t_2\)). Por lo tanto, podemos escribir\[U \left( t _ {2} , t _ {0} \right) = U \left( t _ {2} , t _ {1} \right) U \left( t _ {1} , t _ {0} \right) \label{2.8}\] Nota, ya que\(U\) actúa a la derecha, el orden importa:\[\left.\begin{aligned} | \psi \left( t _ {2} \right) \rangle & = U \left( t _ {2} , t _ {1} \right) U \left( t _ {1} , t _ {0} \right) | \psi \left( t _ {0} \right) \rangle \\[4pt] & = U \left( t _ {2} , t _ {1} \right) | \psi \left( t _ {1} \right) \rangle \end{aligned} \right. \label{2.9}\] Ecuación\ ref {2.8} ya es muy sugerente de una forma exponencial para\(U\). Además, dado que el tiempo es continuo y el operador es lineal, también sugiere que el propagador de tiempo solo depende de un intervalo de tiempo\[U \left( t _ {1} , t _ {0} \right) = U \left( t _ {1} - t _ {0} \right) \label{2.10}\]

4. Reversión de tiempo. La inversa del propagador de tiempo es el operador de inversión de tiempo. De la ecuación\ ref {2.8}:

\[ \begin{align} U \left( t , t _ {0} \right) U \left( t _ {0} , t \right) = &1 \label{2.11} \\[4pt] \therefore \,\, U^{- 1} \left( t , t _ {0} \right) &= U \left( t _ {0} , t \right) . \label{2.12} \end{align}\]

Una ecuación de movimiento para U

Encontremos una ecuación de movimiento que describa al operador de evolución temporal utilizando el cambio del sistema para un paso de tiempo infinitesimal,\(\delta t\):\(U(t+ \delta t)\). Desde

\[\lim _ {\delta t \rightarrow 0} U ( t + \delta t , t ) = 1 \label{2.13}\]

Esperamos que por lo suficientemente pequeños\(\delta t\),\(U\) va a cambiar linealmente con\(\delta t\). Esto se basa en la analogía con el pensamiento del movimiento determinista en los sistemas clásicos. Configurando\(t_0\) a 0, para que\(U(t,t_o) = U(t)\), podamos escribir

\[U ( t + \delta t ) = U (t) - i \hat {\Omega} (t) \delta t \label{2.14}\]

\(\hat{\Omega}\)es un operador hermitiano dependiente del tiempo, el cual se requiere\(U\) para ser unitario. Ahora podemos escribir una ecuación diferencial para el desarrollo del tiempo de\(U(t,t_o)\), la ecuación de movimiento para\(U\):

\[\dfrac {d U (t)} {d t} = \lim _ {\delta t \rightarrow 0} \dfrac {U ( t + \delta t ) - U (t)} {\delta t} \label{2.15}\]

Entonces de la Ecuación\ ref {2.14} tenemos:

\[\dfrac {\partial U \left( t , t _ {0} \right)} {\partial t} = - i \hat {\Omega} U \left( t , t _ {0} \right) \label{2.16}\]

Ahora se puede ver que el operador necesitaba un argumento complejo, porque de lo contrario la densidad de probabilidad no se conservaría; subiría o decairía. Más bien oscila a través de diferentes estados del sistema.

Observamos que\(\hat {\Omega}\) tiene unidades de frecuencia. Dado que la mecánica cuántica asocia fundamentalmente la frecuencia y la energía como\(E = \hbar \omega\), y dado que el hamiltoniano es el operador correspondiente a la energía, y responsable de la evolución del tiempo en la mecánica hamiltoniana, escribimos

\[\hat {\Omega} = \dfrac {\hat {H}} {\hbar} \label{2.17}\]

Con esa sustitución tenemos una ecuación de movimiento para

\[\mathrm {i} \hbar \dfrac {\partial} {\partial t} U \left( t , t _ {0} \right) = \hat {H} U \left( t , t _ {0} \right) \label{2.18}\]

Multiplicar desde la derecha por\(| \psi(t_o) \rangle \) le da al TDSE:

\[i \hbar \dfrac {\partial} {\partial t} | \psi \rangle = \hat {H} | \psi \rangle \label{2.19}\]

Si usas el hamiltoniano para una partícula libre (\(- \left( \hbar^{2} / 2 m \right) \left( \partial^{2} / \partial x^{2} \right)\)), esto parece una ecuación de onda clásica, excepto que es lineal en el tiempo. Más bien, esto parece una ecuación de difusión con constante de difusión imaginaria. También nos interesa la ecuación de movimiento para la\(U^{\dagger}\) que se describe la evolución temporal de las funciones de onda conjugadas. Siguiendo el mismo enfoque y reconociendo que\(U^{\dagger} \left( t , t _ {0} \right)\), actúa a la izquierda:

\[\langle \psi (t) | = \langle \psi \left( t _ {0} \right) | U^{\dagger} \left( t , t _ {0} \right) \label{2.20}\]

obtenemos

\[- i \hbar \dfrac {\partial} {\partial t} U^{\dagger} \left( t , t _ {0} \right) = U^{\dagger} \left( t , t _ {0} \right) \hat {H} \label{2.21}\]

Evaluación del Operador de Evolución del Tiempo

A primera vista puede parecer sencillo integrar la Ecuación\ ref {2.18}. Si\(H\) es una función del tiempo, entonces la integración de\(i \hbar \dfrac{d U}{U} = H\, dt\) da

\[U \left( t , t _ {0} \right) = \exp \left[ \frac {- i} {\hbar} \int _ {t _ {0}}^{t} H \left( t^{\prime} \right) d t^{\prime} \right] \label{2.22}\]

Siguiendo nuestra definición anterior del propagador del tiempo, este exponencial se lanzaría como una expansión en serie

\[U \left( t , t _ {0} \right)^{2} = 1 - \frac {i} {\hbar} \int _ {t _ {0}}^{t} H \left( t^{\prime} \right) d t^{\prime} + \frac {1} {2 !} \left( \frac {- i} {\hbar} \right)^{2} \int _ {t _ {0}}^{t} d t^{\prime} d t^{\prime \prime} H \left( t^{\prime} \right) H \left( t^{\prime \prime} \right) + \ldots \label{2.23}\]

Este enfoque es peligroso, ya que no estamos tratando adecuadamente\(H\) como operador. Mirando el segundo término en la Ecuación\ ref {2.23}, vemos que esta expresión se integra sobre ambos posibles ordenamientos de tiempo de las dos operaciones hamiltonianas, lo que solo sería apropiado si los hamiltonianos en diferentes momentos conmutan:\( H(t'),H(t'')] =0\)

Ahora, procedamos un poco más cuidadosamente asumiendo que los hamiltonianos en diferentes momentos no se desplazan. Integrando la ecuación\ ref {2.18} directamente de\(t_0\) a\(t\) da

\[U \left( t , t _ {0} \right) = 1 - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau H ( \tau ) U \left( \tau , t _ {0} \right) \label{2.24}\]

Esta es la solución; sin embargo, no es muy práctica ya que\(U(t,t_o)\) es una función de sí misma. Pero podemos hacer una expansión iterativa mediante la sustitución repetitiva de\(U\) dentro de sí mismo. El primer paso en este proceso es

\[\begin{align} U \left( t , t _ {0} \right) &= 1 - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau H ( \tau ) \left[ 1 - \frac {i} {\hbar} \int _ {t _ {0}}^{\tau} d \tau^{\prime} H \left( \tau^{\prime} \right) U \left( \tau^{\prime} , t _ {0} \right) \right] \\[4pt] & = 1 + \left( \frac {- i} {\hbar} \right) \int _ {t _ {0}}^{t} d \tau H ( \tau ) + \left( \frac {- i} {\hbar} \right)^{2} \int _ {t _ {0}}^{t} d \tau \int _ {t _ {0}}^{\tau} d \tau^{\prime} H ( \tau ) H \left( \tau^{\prime} \right) U \left( \tau^{\prime} , t _ {0} \right)\end{align} \label{2.25}\]

Obsérvese en el último término de esta ecuación, que los límites de integración imponen un orden de tiempo; es decir, la primera variable de integración\(\tau'\) debe preceder a la segunda\(\tau\). Pictorialmente, el área de integración es

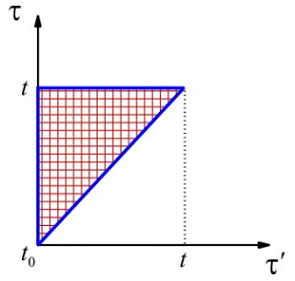
El siguiente paso de sustitución da

\[\begin{align} U \left( t , t _ {0} \right) & = 1 + \left( \frac {- i} {\hbar} \right) \int _ {t _ {0}}^{t} d \tau H ( \tau ) \nonumber \\[4pt] & + \left( \frac {- i} {\hbar} \right)^{2} \int _ {t _ {0}}^{t} d \tau \int _ {t _ {0}}^{\tau} d \tau^{\prime} H ( \tau ) H \left( \tau^{\prime} \right) \label{2.26} \\[4pt] & + \left( \frac {- i} {\hbar} \right)^{3} \int _ {t _ {0}}^{t} d \tau \int _ {t _ {0}}^{\tau} d \tau^{\prime} \int _ {t _ {0}}^{t^{\prime}} d \tau^{\prime \prime} H ( \tau ) H \left( \tau^{\prime} \right) H \left( \tau^{\prime \prime} \right) U \left( \tau^{\prime \prime} , t _ {0} \right) \nonumber \end{align}\]

A partir de esta expansión, debes estar consciente de que hay un orden de tiempo para las interacciones. Para el tercer término,\(\tau^{\prime \prime}\) actúa ante\(\tau^{\prime}\), que actúa ante\(\tau\):\(t _ {0} \leq \tau^{\prime \prime} \leq \tau^{\prime} \leq \tau \leq t\)

¿Qué representa esta expresión? Imagina que estás iniciando en estado\(| \psi _ {0} \rangle = | \ell \rangle\) y quieres describir cómo evoluciona uno hacia un estado objetivo\(| \psi \rangle = | k \rangle\). Los posibles caminos por los cuales se puede desplazar la amplitud y evolucionar la fase, que se representan en términos de estas variables de tiempo son:

El primer término en la Ecuación\ ref {2.26} representa todas las acciones del hamiltoniano que actúan para acoplar directamente\(| \ell \rangle\) y\(| k \rangle\). El segundo término describió posibles transiciones de\(| \ell \rangle\) a\(| k \rangle\) vía de un estado intermedio\(| m \rangle\). La expresión for\(U\) describe todos los caminos posibles entre el estado inicial y final. Cada uno de estos caminos interfiere en formas dictadas por la fase adquirida de nuestros propios estados bajo el hamiltoniano dependiente del tiempo.

La solución para\(U\) obtenida de esta sustitución iterativa se conoce como el exponencial positivo ordenado por el tiempo

\[\left.\begin{aligned} U \left( t , t _ {0} \right) & = 1 + \left( \frac {- i} {\hbar} \right) \int _ {t _ {0}}^{t} d \tau H ( \tau ) \\[4pt] & + \left( \frac {- i} {\hbar} \right)^{2} \int _ {t _ {0}}^{t} d \tau \int _ {t _ {0}}^{\tau} d \tau^{\prime} H ( \tau ) H \left( \tau^{\prime} \right) \\[4pt] & + \left( \frac {- i} {\hbar} \right)^{3} \int _ {t _ {0}}^{t} d \tau \int _ {t _ {0}}^{\tau} d \tau^{\prime} \int _ {t _ {0}}^{t^{\prime}} d \tau^{\prime \prime} H ( \tau ) H \left( \tau^{\prime} \right) H \left( \tau^{\prime \prime} \right) U \left( \tau^{\prime \prime} , t _ {0} \right) \end{aligned} \right. \label{2.27}\]

(\(\hat{T}\)se conoce como el operador de orden de tiempo de Dyson.) En esta expresión el orden del tiempo es

\[\left. \begin{array} {l} {t _ {0} \rightarrow \tau _ {1} \rightarrow \tau _ {2} \rightarrow \tau _ {3} \dots \tau _ {n} \rightarrow t} \\[4pt] {t _ {0} \rightarrow \quad \dots \quad \tau^{\prime \prime} \rightarrow \tau^{\prime} \rightarrow \tau} \end{array} \right.\label{2.28}\]

Entonces, esta expresión te habla de cómo evoluciona un sistema cuántico a lo largo de un intervalo de tiempo dado, y permite cualquier trayectoria posible desde un estado inicial hasta un estado final a través de cualquier número de estados intermedios. Cada término en la expansión explica más transiciones posibles entre diferentes estados cuánticos intermedios durante esta trayectoria.

Compare el exponencial ordenado por el tiempo con la expansión tradicional de un exponencial:

\[1 + \sum _ {n = 1}^{\infty} \frac {1} {n !} \left( \frac {- i} {\hbar} \right)^{n} \int _ {t _ {0}}^{t} d \tau _ {n} \ldots \int _ {t _ {0}}^{t} d \tau _ {1} H \left( \tau _ {n} \right) H \left( \tau _ {n - 1} \right) \ldots H \left( \tau _ {1} \right) \label{2.29}\]

Aquí las variables de tiempo asumen todos los valores, y por lo tanto\(H(t,t_0)\) se calculan todos los ordenamientos para. Las áreas se normalizan por el\(n!\) factor (hay\(n!\) ordenamientos de tiempo de los\(t_n\) tiempos). (Como se comentó anteriormente estos puntos necesitan alguna aclaración más.) También nos interesa el conjugado hermitiano de\(U \left( t , t _ {0} \right)\), que tiene la ecuación de movimiento en la Ecuación\ ref {2.21}. Si repetimos el método anterior, recordando eso\(U^{\dagger} \left( t , t _ {0} \right)\), actúa a la izquierda, entonces obtenemos

\[U^{\dagger} \left( t , t _ {0} \right) = 1 + \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau U^{\dagger} ( t , \tau ) H ( \tau ) \label{2.30}\]

Realizar una sustitución iterativa conduce a un exponencial negativo ordenado en el tiempo:

\[U^{\dagger} \left( t , t _ {0} \right) = 1 + \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau U^{\dagger} ( t , \tau ) H ( \tau )\label{2.31}\]

Aquí el\(H(\tau_i)\) acto a la izquierda.

Lecturas

1. Cohen-Tannoudji, C.; Diu, B.; Lalöe, F., Mecánica Cuántica. Wiley-Interscience: París, 1977; p. 1340.
2. Merzbacher, E., Mecánica Cuántica. 3a ed.; Wiley: Nueva York, 1998; Ch. 14.
3. Mukamel, S., Principios de Espectroscopia Óptica No Lineal. Oxford University Press: Nueva York, 1995; Cap. 2.
4. Sakurai, J. J., Mecánica Cuántica Moderna, Edición Revisada. Addison-Wesley: Reading, MA, 1994; Ch. 2.