3.2: Integración directa de la ecuación de Schrödinger

Bien, ¿cómo evaluamos el propagador de tiempo y obtenemos una trayectoria dependiente del tiempo para un sistema cuántico? Expresiones como los exponenciales ordenados por el tiempo son desalentadoras, y no hay formas sencillas de manejar esto. No se puede truncar lo exponencial porque generalmente no se trata de una serie que converge rápidamente. También, las soluciones oscilan rápidamente como resultado de la fase adquirida a la energía de los estados involucrados, lo que lleva a un formidable problema de integración. Las oscilaciones rápidas requieren pequeños pasos de tiempo, cuando de hecho las escalas de tiempo. Por ejemplo, en un problema de dinámica molecular, las oscilaciones de mayor frecuencia pueden ser el resultado de estados electrónicamente excitados con períodos de menos de un femtosegundo, y la dinámica nuclear que se espera describir puede ocurrir en muchas escalas de tiempo de picosegundos. Más que recetas generales, existe un arsenal de diferentes estrategias que se adaptan a tipos particulares de problemas. La elección de cómo proceder generalmente viene dictada por los detalles de su problema, y a menudo es una forma de arte. Se necesita hacer un esfuerzo considerable para formular el problema, particularmente eligiendo una base adecuada para su problema. Aquí nuestro objetivo es obtener una idea de los tipos de estrategias disponibles, trabajando principalmente con los principios, en lugar de los detalles de cómo se implementa.

Comencemos discutiendo el enfoque más general. Con recursos computacionales adecuados, podemos elegir el enfoque de fuerza bruta de integración numérica. Comenzamos por elegir un conjunto de bases y definir el estado inicial\(\psi_0\). Luego, podemos evaluar numéricamente la dependencia temporal de la función de onda a lo largo de un período\(t\) de tiempo discretizando el tiempo en\(n\) pequeños pasos de ancho\(\delta t = t / n\) sobre los cuales el cambio del sistema es pequeño. Una variedad de estrategias se pueden concretar en la práctica.

Una posibilidad es ampliar su función de onda en el conjunto de bases de su elección

\[| \psi (t) \rangle = \sum _ {n} c _ {n} (t) | \varphi _ {n} \rangle \label{2.32}\]

y resolver por la dependencia temporal de los coeficientes de expansión. Sustituyendo en el lado derecho del TDSE,

\[i \hbar \frac {\partial} {\partial t} | \psi \rangle = \hat {H} | \psi \rangle \label{2.33}\]

y luego actuar desde la izquierda por ambos\(\langle k |\) lados conduce a una ecuación que describe su dependencia del tiempo:

\[i \hbar \frac {\partial c _ {k} (t)} {\partial t} = \sum _ {n} H _ {k n} (t) c _ {n} (t) \label{2.34}\]

o en forma de matriz\(i \hbar \dot {c} = H c\). Esto representa un conjunto de ecuaciones diferenciales acopladas de primer orden en las que la amplitud fluye entre diferentes estados base a velocidades determinadas por los elementos de la matriz del hamiltoniano dependiente del tiempo. Tales ecuaciones son sencillas de integrar numéricamente. Reconocemos que podemos integrarnos en una grilla si el paso de tiempo adelante (\(\delta t\)) es lo suficientemente pequeño como para que el hamiltoniano sea esencialmente constante. Entonces la Ecuación\ ref {2.34} se convierte

\[i \hbar \delta c _ {k} (t) = \sum _ {n} H _ {k n} (t) c _ {n} (t) \delta t \label{2.35}\]

y el sistema se propaga como

\[c _ {k} ( t + \delta t ) = c _ {k} (t) + \delta c _ {k} (t) \label{2.36}\]

La desventaja de tal cálculo son los pasos de tiempo inusualmente pequeños y el costo computacional significativo requerido.

Del mismo modo, podemos usar una cuadrícula con pasos de tiempo cortos para simplificar nuestro propagador de tiempo como

\[\hat {U} ( t + \delta t , t ) = \exp \left[ - \frac {i} {\hbar} \int _ {t}^{t + \delta t} d t^{\prime} \hat {H} \left( t^{\prime} \right) \right] \approx \exp \left[ - \frac {i} {\hbar} \delta t \hat {H} (t) \right] \label{2.37}\]

Por lo tanto, el propagador de tiempo puede escribirse como un producto de\(n\) propagadores a lo largo de estos pequeños intervalos.

\[\begin{align} \hat {U} (t) & = \lim _ {\delta t \rightarrow 0} \left[ \hat {U} _ {n} \hat {U} _ {n - 1} \cdots \hat {U} _ {2} \hat {U} _ {1} \right] \label{2.38A} \\[4pt] & = \lim _ {n \rightarrow \infty} \prod _ {j = 0}^{n - 1} \hat {U} _ {j} \label{2.38B} \end{align}\]

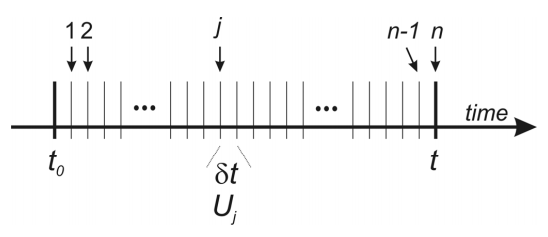
Aquí la propagación del tiempo sobre el j ^ésimo paso de tiempo pequeño es

\[\left.\begin{aligned} \hat {U} _ {j} & = \exp \left[ - \frac {i} {\hbar} \delta t \hat {H} _ {j} \right] \\[4pt] \hat {H} _ {j} & = \hat {H} ( j \delta t ) \end{aligned} \right. \label{2.39}\]

Tenga en cuenta que las expresiones en Ecuaciones\ ref {2.38A} y\ ref {2.38B} son operadores ordenados por tiempo de derecha a izquierda, que denotamos con el subíndice “+”. Aunque la Ecuación\ ref {2.38B} es exacta en el límite\(\delta t \rightarrow 0\) (o\(n→∞\)), podemos elegir un número finito tal que\(H(t)\) no cambie mucho con el tiempo\(\delta t\). En este límite el tiempo propagador no cambia mucho y puede aproximarse como una expansión

\[\hat {U} _ {j} \approx 1 - \frac {i} {\hbar} \delta t \hat {H} _ {j} \label{2.40}.\]

En un sentido general este enfoque no es muy práctico. La primera razón es que el paso de tiempo está determinado por el\(\delta \mathrm {t} < \hbar / | H |\) cual suele ser muy pequeño en comparación con la dinámica de interés. La segunda complicación surge cuando los operadores de energía potencial y cinética en el Hamiltoniano no conmutan. Tomando al hamiltoniano para ser\(\hat {H} = \hat {T} + \hat {V}\)

\[\left.\begin{aligned} e^{- i \hat {H} (t) \delta t / h} & = e^{- i ( \hat {T} (t) + \hat {V} (t) ) \delta t / h} \\[4pt] & \approx e^{- i \hat {T} (t) \delta t / \hbar} e^{- i \hat {V} (t) \delta t / h} \end{aligned} \right. \label{2.41}\]

La segunda línea hace la aproximación del Operador Split, lo que establece que el propagador de tiempo durante un período suficientemente corto puede aproximarse como un producto de propagadores independientes que evolucionan el sistema sobre la energía cinética y potencial. La validez de esta aproximación depende de qué tan bien se conmuten estos operadores y del paso de tiempo, con el error escalado como\(\frac {1} {2} [ \hat {T} (t) , \hat {V} (t) ] ( \delta t / \hbar )^{2}\) significado que debemos usar un paso de tiempo, tal que\(\delta t < \left\{2 \hbar^{2} / [ \hat {T} (t) , \hat {V} (t) ] \right\}^{1 / 2}\)

Esta aproximación se puede mejorar simetrizando el operador de división como

\[e^{- i \hat {H} (t) \delta t / h} \approx e^{- i \hat {V} (t) \frac {\delta t} {2} / h} e^{- i \hat {T} (t) \delta t / h} e^{- i \hat {V} (t) \frac {\delta t} {2} / h} \label{2.42}\]

Aquí el error escala como\(\frac {1} {12} ( \delta t / \hbar )^{3} \left\{[ \hat {T} , [ \hat {T} , \hat {V} ] ] + \frac {1} {2} [ \hat {V} , [ \hat {V} , \hat {T} ] ] \right\}\). No hay un incremento significativo en el esfuerzo computacional ya que la mitad de las operaciones se pueden combinar como

\[e^{- \frac {i \hat {V}} {h} \frac {( j + 1 ) \delta t} {2}} e^{- \frac {i \hat {V}} {\hbar} \frac {j \delta t} {2}} \approx e^{- i \hat {V} j \delta t / \hbar}\]

para dar\( U (t) \approx e^{- i \hat {V} \frac {n \delta t} {2} / h} \left[ \prod _ {j = 1}^{n} e^{- i \hat {V} j \delta t / h} e^{- i \hat {T} j \delta t / h} \right] e^{- i \hat {V} \frac {\delta t} {2} / h} \label{2.44}\)

Lecturas

1. Tannor, D. J., Introducción a la mecánica cuántica: una perspectiva dependiente del tiempo. Libros de Ciencias Universitarias: Sausilito, CA, 2007.