7.2: Interacciones Clásicas Luz-Materia

Ondas electromagnéticas de plano clásico

Como punto de partida, es útil resumir primero la descripción clásica de los campos electromagnéticos. Una derivación de las soluciones de onda plana a los campos eléctricos y magnéticos y al potencial vectorial se describe en el apéndice en la Sección 6.6.

Las ecuaciones de Maxwell describen los campos eléctricos (\(\overline {E}\)) y magnéticos (\(\overline {B}\)); sin embargo, para construir un hamiltoniano, debemos usar el potencial de interacción dependiente del tiempo (en lugar de un campo). Para construir la representación potencial de\(\overline {E}\) y\(\overline {B}\), se necesita un potencial\(\overline {A} ( \overline {r} , t )\) vectorial y un potencial escalar\(\varphi ( \overline {r} , t )\). Para la electrostática normalmente pensamos que el campo está relacionado con el potencial electrostático a través\(\overline {E} = - \nabla \varphi\), pero para un campo que varía en el tiempo y en el espacio, el potencial electrodinámico debe expresarse en términos de ambos\(\overline {A}\) y\(\varphi\).

En general, una onda electromagnética escrita en términos de los campos eléctrico y magnético requiere seis variables (la\(x\),\(y\), y\(z\) componentes de\(E\) y\(B\)). Este es un problema sobredeterminado; las ecuaciones de Maxwell los limitan. La representación potencial tiene cuatro variables (\(A _ {x}\),\(A _ {y}\)\(A _ {z}\), y\(\varphi\)), pero estas aún no están determinadas de manera única. Elegimos una restricción, una representación o calibre, que nos permita describir de manera única la onda. Elegir un calibre tal que\(\varphi=0\) (es decir, el calibre Coulomb) conduzca a una descripción única de\(\overline {E}\) y\(\overline {B}\):

\[- \overline {\nabla}^{2} \overline {A} ( \overline {r} , t ) + \frac {1} {c^{2}} \frac {\partial^{2} \overline {A} ( \overline {r} , t )} {\partial t^{2}} = 0 \label{6.4}\]

y

\[\overline {\nabla} \cdot \overline {A} = 0 \label{6.5)}\]

Esta ecuación de onda para el potencial vectorial proporciona una solución de onda plana para espacio libre de carga y condiciones de límite adecuadas:

\[\overline {A} ( \overline {r} , t ) = A _ {0} \hat {\varepsilon} e^{i ( \overline {k} \cdot \overline {r} - \omega t )} + A _ {0}^{*} \hat {\varepsilon} e^{- i ( \overline {k} \cdot \overline {r} - \omega t )} \label{6.6}\]

Esto describe la onda oscilando en el tiempo a una frecuencia angular\(\omega\) y propagándose en el espacio en la dirección a lo largo del vector de onda\(\overline {k}\), con un periodo espacial\(\lambda = 2 \pi / | \overline {k} |\). Escribiendo la relación entre\(k\)\(\omega\), y\(\lambda\) en un medio con índice de refracción\(n\) en términos de sus valores en el espacio libre:

\[k = n k _ {0} = \frac {n \omega _ {0}} {c} = \frac {2 \pi n} {\lambda _ {0}} \label{6.7}\]

La onda tiene una amplitud\(A_0\), que se dirige a lo largo del vector de unidad de polarización\(\overline {k}\). Ya que\(\overline {\nabla} \cdot \overline {A} = 0\), vemos eso\(\overline {k} \cdot \hat {\mathcal {E}} = 0\) o\(\overline {k} \perp \hat {\mathcal {E}}\). A partir del potencial vectorial podemos obtener\(\overline {E}\) y\(\overline {B}\)

\[\begin{align} \overline {E} & = - \frac {\partial \overline {A}} {\partial t} \\[4pt] & = i \omega A _ {0} \hat {\varepsilon} \left( e^{i ( \overline {k} \cdot \overline {r} - \omega t )} - e^{- i ( \overline {k} \cdot \overline {r} - \omega t )} \right) \label{6.8} \end{align}\]

\[ \begin{align} \overline {B} & = \overline {\nabla} \times \overline {A} \\[4pt] & = i ( \overline {k} \times \hat {\varepsilon} ) A _ {0} \left( e^{i ( \overline {k} \cdot \overline {r} - \omega t )} - e^{- i ( \overline {k} \cdot \overline {r} - \omega t )} \right) \label{6.9} \end{align}\]

Si definimos un vector unitario a lo largo de la polarización del campo magnético como

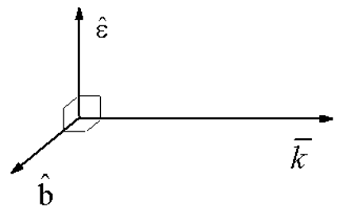
\[\hat {b} = ( \overline {k} \times \hat {\mathcal {\varepsilon}} ) / | \overline {k} | = \hat {k} \times \hat {\mathcal {E}},\]

vemos que el vector de onda, la polarización del campo eléctrico y la polarización del campo magnético son mutuamente ortogonales\(\hat {k} \perp \hat {\varepsilon} \perp \hat {b}\).

Además, al comparar la Ecuación\ ref {6.6} y\ ref {6.8} vemos que el potencial vectorial oscila como\(\cos(\omega t)\), mientras que los campos eléctricos y magnéticos oscilan como\(\sin(\omega t)\). Si definimos

\[\frac {1} {2} E _ {0} = i \omega A _ {0} \label{6.10}\]

\[\frac {1} {2} B _ {0} = i | k | A _ {0} \label{6.11}\]

entonces,

\[\overline {E} ( \overline {r} , t ) = \left| E _ {0} \right| \hat {\varepsilon} \sin ( \overline {k} \cdot \overline {r} - \omega t ) \label{6.12}\]

\[\overline {B} ( \overline {r} , t ) = \left| B _ {0} \right| \hat {b} \sin ( \overline {k} \cdot \overline {r} - \omega t ) \label{6.13}\]

Tenga en cuenta que

\[E _ {0} / B _ {0} = \omega / | k | = c.\]

Vamos a querer expresar la amplitud del campo de una manera que sea experimentalmente accesible. La intensidad\(I\), el flujo de energía a través de una unidad de área, se mide más fácilmente. Es el valor promediado en el tiempo del vector Poynting

\[I = \langle \overline {S} \rangle = \frac {1} {2} \varepsilon _ {0} c E _ {0}^{2} \quad \left( \mathrm {W} / \mathrm {m}^{2} \right) \label{6.15}\]

Una representación alternativa de la amplitud que es útil para describir los campos de luz cuántica es la densidad de energía

\[U = \frac {I} {c} = \frac {1} {2} \varepsilon _ {0} E _ {0}^{2} \quad \left( \mathrm {J} / \mathrm {m}^{3} \right) \label{6.16}\]

Hamiltoniano clásico para campo de radiación que interactúa con partículas cargadas

Ahora, obtenemos un hamiltoniano clásico que describe partículas cargadas que interactúan con un campo de radiación en términos del potencial vectorial. Comience con la fuerza Lorentz sobre una partícula con carga\(q\):

\[\overline {F} = q ( \overline {E} + \overline {v} \times \overline {B} ) \label{6.17}\]

Aquí v es la velocidad de la partícula. Escribiendo esto para one direction (\(x\)) en términos de los componentes cartesianos de\(\overline {E}\)\(\overline {v}\)\(\overline {B}\), y, tenemos:

\[F _ {x} = q \left( E _ {x} + v _ {y} B _ {z} - v _ {z} B _ {y} \right) \label{6.18}\]

En la mecánica lagrangiana, esta fuerza se puede expresar en términos de la energía potencial total

\[F _ {x} = - \frac {\partial U} {\partial x} + \frac {d} {d t} \left( \frac {\partial U} {\partial v _ {x}} \right) \label{6.19}\]

Usando las relaciones que describen\(\overline {E}\) y\(\overline {B}\) en términos de\(\overline {A}\) y\(\varphi \) (Ecuaciones\ ref {6.10} y\ ref {6.11}), insertando en la Ecuación\ ref {6.18}, y trabajándola en la forma de Ecuación\ ref {6.19}, podemos demostrar que

\[U = q \varphi - q \overline {v} \cdot \overline {A} \label{6.20}\]

Esto se deriva en otra parte ⁴ y se confirma fácilmente reemplazándolo en la Ecuación\ ref {6.19}. Ahora podemos escribir un lagrangiano en términos de la energía cinética y potencial de la partícula

\[\begin{align} L &= T - U \label{6.21} \\[4pt] &= \frac {1} {2} m \overline {v}^{2} + q \overline {v} \cdot \overline {A} - q \varphi \label{6.22} \end{align}\]

El hamiltoniano clásico se relaciona con el lagrangiano como

\[\begin{align} H & = \overline {p} \cdot \overline {v} - L \\[4pt] & = \overline {p} \cdot \overline {v} - \frac {1} {2} m \overline {v}^{2} - q \overline {v} \cdot \overline {A} - q \varphi \label{6.23} \end{align}\]

Reconociendo

\[\overline {p} = \frac {\partial L} {\partial \overline {v}} = m \overline {v} + q \overline {A} \label{6.24}\]

escribimos

\[\overline {v} = \frac {1} {m} ( \overline {p} - q \overline {A} ) \label{6.25}\]

Ahora sustituyendo Ecuaciones\ ref {6.25} en Ecuación\ ref {6.23}, tenemos

\[ \begin{align} H &= \frac {1} {m} \overline {p} \cdot ( \overline {p} - q \overline {A} ) - \frac {1} {2 m} ( \overline {p} - q \overline {A} )^{2} - \frac {q} {m} ( \overline {p} - q \overline {A} ) \cdot A + q \varphi \label{6.26} \\[4pt] &= \frac {1} {2 m} [ \overline {p} - q \overline {A} ( \overline {r} , t ) ]^{2} + q \varphi ( \overline {r} , t ) \label{6.27} \end{align}\]

Este es el hamiltoniano clásico para una partícula en un campo electromagnético. En el calibre Coulomb (\(\varphi = 0\)), se baja el último término.

Podemos escribir un hamiltoniano para una sola partícula en un potencial ligado\(V_0\) en ausencia de un campo externo como

\[H _ {0} = \frac {\overline {p}^{2}} {2 m} + V _ {0} ( \overline {r} ) \label{6.28}\]

y en presencia del campo EM,

\[H = \frac {1} {2 m} ( \overline {p} - q \overline {A} ( \overline {r} , t ) )^{2} + V _ {0} ( \overline {r} ) \label{6.29}\]

Ampliando obtenemos

\[H = H _ {0} - \frac {q} {2 m} ( \overline {p} \cdot \overline {A} + \overline {A} \cdot \overline {p} ) + \frac {q^{2}} {2 m} | \overline {A} ( \overline {r} , t ) |^{2} \label{6.30}\]

Generalmente el último término que va como el cuadrado de\(A\) es pequeño en comparación con el término cruzado, que es proporcional al primer poder de\(A\). Este término debe considerarse para una intensidad de campo extremadamente alta, que no es perturbadora y distorsiona significativamente las moléculas de unión potenciales entre sí, es decir, cuando es similar en magnitud a\(V_0\). Se puede estimar que esto comenzaría a jugar un papel en los niveles de intensidad\(>10^{15}\, W/cm^2\), lo que puede observarse para láseres de femtosegundos pulsados de muy alta energía y fuertemente enfocados. Entonces, para los campos débiles tenemos una expresión que se mapea directamente sobre soluciones que podemos formular en la imagen de interacción:

\[H = H _ {0} + V (t) \label{6.31}\]

con

\[V (t) = \frac {q} {2 m} ( \overline {p} \cdot \overline {A} + \overline {A} \cdot \overline {p} ) \label{6.32}.\]

Lecturas

1. Cohen-Tannoudji, C.; Diu, B.; Lalöe, F., Mecánica Cuántica. Wiley-Interscience: París, 1977; Apéndice III.
2. Jackson, J. D., Electrodinámica clásica. 2ª ed.; John Wiley and Sons: Nueva York, 1975.
3. McHale, J. L., Espectroscopia Molecular. 1a ed.; Prentice Hall: Upper Saddle River, NJ, 1999.
4. Merzbacher, E., Mecánica Cuántica. 3a ed.; Wiley: Nueva York, 1998.
5. Sakurai, J. J., Mecánica Cuántica Moderna, Edición Revisada. Addison-Wesley: Reading, MA, 1994.
6. Schatz, G. C.; Ratner, M. A., Mecánica Cuántica en Química. Publicaciones de Dover: Mineola, NY, 2002; pp. 82-83.