10.1: Definiciones, propiedades y ejemplos de funciones de correlación

Volviendo a las fluctuaciones microscópicas de una variable molecular\(A\), parece haber poca información en la observación de la trayectoria de una variable que caracteriza el comportamiento dependiente del tiempo de una molécula individual. Sin embargo, esta dinámica no es del todo aleatoria, ya que son consecuencia de interacciones dependientes del tiempo con el entorno. Podemos proporcionar una descripción estadística de las escalas de tiempo características y amplitudes a estos cambios comparando el valor de\(A\) en tiempo\(t\) con el valor de\(A\) en tiempo\(t’\) posterior.

Figura\(\PageIndex{1}\): Fluctuaciones\(A\) en el tiempo alrededor de un promedio\(\langle A \rangle \).

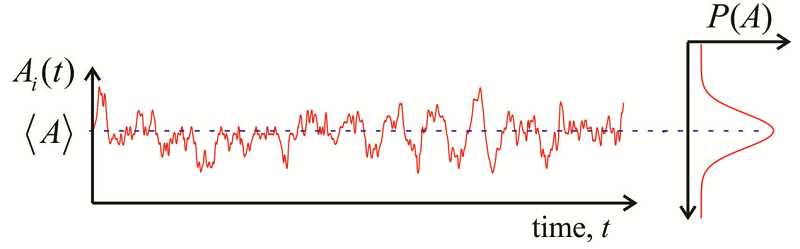
Definimos una función de correlación de tiempo (TCF) como una cantidad dependiente del tiempo\(A(t)\), multiplicada por esa cantidad en algún momento posterior\(A(t')\), y promediada sobre un conjunto de equilibrio:

\[C _ {A A} \left( t , t^{\prime} \right) \equiv \left\langle A (t) A \left( t^{\prime} \right) \right\rangle _ {e q}\label{9.1}\]

La forma clásica de la función de correlación se evalúa como

\[C _ {A A} \left( t , t^{\prime} \right) = \int d \mathbf {p} \int d \mathbf {q} A ( \mathbf {p} , \mathbf {q} ; t ) A \left( \mathbf {p} , \mathbf {q} ; t^{\prime} \right) \rho _ {e q} ( \mathbf {p} , \mathbf {q} ) \label{9.2}\]

mientras que la función de correlación cuántica puede evaluarse como

\[\begin{align} C _ {A A} \left( t , t^{\prime} \right) &= \operatorname {Tr} \left[ \rho _ {e q} A (t) A \left( t^{\prime} \right) \right] \\[4pt] &= \sum _ {n} p _ {n} \left\langle n \left| A (t) A \left( t^{\prime} \right) \right| n \right\rangle \label{9.3} \end{align}\]

donde

\[p _ {n} = e^{- \beta E _ {n}} / Z.\]

Se trata de funciones de autocorrelación, que correlaciona la misma variable en dos momentos del tiempo, pero también se puede definir una función de correlación cruzada que describa la correlación de dos variables diferentes en el tiempo

\[C _ {A B} \left( t , t^{\prime} \right) \equiv \left\langle A (t) B \left( t^{\prime} \right) \right\rangle \label{9.4}\]

Entonces, ¿qué nos dice una función de correlación de tiempo? Cualitativamente, un TCF describe cuánto tiempo persiste una propiedad dada de un sistema hasta que es promediada por movimientos microscópicos e interacciones con su entorno. Describe cómo y cuándo se ha desvanecido una relación estadística. Podemos usar funciones de correlación para describir diversos procesos químicos dependientes del tiempo. Por ejemplo, utilizaremos\(\langle \mu (t) \mu ( 0 ) \rangle\) -la dinámica del momento dipolar molecular- para describir la espectroscopia de absorción. También los usaremos para procesos de relajación inducidos por la interacción de un sistema y baño:

\[\left\langle H _ {S B} (t) H _ {S B} ( 0 ) \right\rangle.\]

Clásicamente, puede utilizar los TCF para caracterizar los procesos de transporte. Por ejemplo, un coeficiente de difusión está relacionado con la función de correlación de velocidad:

\[D = \frac {1} {3} \int _ {0}^{\infty} d t \langle v (t) v ( 0 ) \rangle.\]

Propiedades de las funciones de correlación

Una función de correlación típica para las fluctuaciones aleatorias en el equilibrio térmico en la variable\(A\) podría parecer

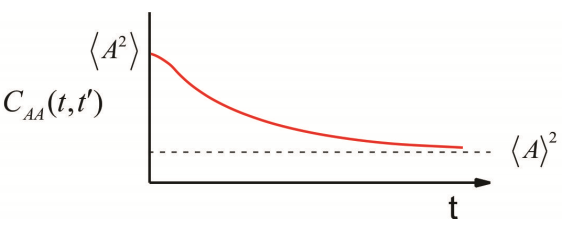
Se describe por una serie de propiedades:

1. Cuando se evalúa en\(t = t’\), obtenemos la amplitud máxima, el valor cuadrático medio de\(A\), que es positivo para una función de autocorrelación e independiente del tiempo. \[C _ {A A} ( t , t ) = \langle A (t) A (t) \rangle = \left\langle A^{2} \right\rangle \geq 0 \label{9.5}\]
2. Para separaciones de largo tiempo, a medida que las fluctuaciones térmicas actúan para aleatorizar el sistema, los valores de A se vuelven no correlacionados\[\lim _ {t \rightarrow \infty} C _ {A A} \left( t , t^{\prime} \right) = \langle A (t) \rangle \left\langle A \left( t^{\prime} \right) \right\rangle = \langle A \rangle^{2} \label{9.6}\]
3. Al tratarse de una cantidad de equilibrio, las funciones de correlación son estacionarias. Eso significa que no dependen del punto absoluto de observación (\(t\)y\(t’\)), sino del intervalo de tiempo entre las observaciones. Un proceso aleatorio estacionario significa que el punto de referencia puede ser desplazado por un valor arbitrario\(T\)\[C _ {A A} \left( t , t^{\prime} \right) = C _ {A A} \left( t + T , t^{\prime} + T \right) \label{9.7}\] Entonces, eligiendo\(T = - t^{\prime}\) y definiendo el intervalo de tiempo\(\tau \equiv t - t^{\prime}\), vemos que solo\(\tau\) importa\[C _ {A A} \left( t , t^{\prime} \right) = C _ {A A} \left( t - t^{\prime} , 0 \right) = C _ {A A} ( \tau ) \label{9.8}\] Implícito en esta afirmación es un entendimiento de que tomamos el promedio de tiempo valor de\(A\) ser igual al conjunto de equilibrio valor promedio de\(A\), es decir, el sistema es ergódico. Entonces, la correlación de fluctuaciones se puede expresar como un promedio de tiempo sobre una trayectoria de una molécula\[\overline {A (t) A ( 0 )} = \lim _ {T \rightarrow \infty} \frac {1} {T} \int _ {0}^{T} d \tau A _ {i} ( t + \tau ) A _ {i} ( \tau ) \label{9.9}\] o un promedio de conjunto de equilibrio\[\langle A (t) A ( 0 ) \rangle = \sum _ {n} \frac {e^{- \beta E _ {n}}} {Z} \langle n | A (t) A ( 0 ) | n \rangle \label{9.10}\]
4. Las funciones clásicas de correlación son reales e incluso en el tiempo:\[\begin{align} \left\langle A (t) A \left( t^{\prime} \right) \right\rangle &= \left\langle A \left( t^{\prime} \right) A (t) \right\rangle \\[4pt] C _ {A A} ( \tau ) &= C _ {A A} ( - \tau ) \label{9.11} \end{align}\]
5. Cuando observamos fluctuaciones sobre un promedio (Figura\(\PageIndex{1}\)), a menudo redefinimos la función de correlación en términos de la desviación de la media\[\delta A \equiv A - \langle A \rangle \label{9.12}\] y\[C _ {\delta A \delta A} (t) = \langle \delta A (t) \delta A ( 0 ) \rangle = C _ {A A} (t) - \langle A \rangle^{2} \label{9.13}\] Ahora vemos que el límite de tiempo largo cuando se pierde la correlación\[\lim _ {t \rightarrow \infty} C _ {\delta A \delta A} (t) = 0\] y el valor de tiempo cero es solo la varianza\[C _ {\delta A \delta A} ( 0 ) = \left\langle \delta A^{2} \right\rangle = \left\langle A^{2} \right\rangle - \langle A \rangle^{2} \label{9.14}\]
6. La escala de tiempo característica de un proceso aleatorio es el tiempo de correlación,\(\tau _ {c}\). Esto caracteriza la escala de tiempo para que TCF se descomponga a cero. Podemos obtener\(\tau _ {c}\) de\[\tau _ {c} = \frac {1} {\left\langle \delta A^{2} \right\rangle} \int _ {0}^{\infty} d t \langle \delta A (t) \delta A ( 0 ) \rangle \label{9.15}\] lo que debería ser evidente si tienes una forma exponencial\[C (t) = C ( 0 ) \exp \left( - t / \tau _ {c} \right).\]

Ejemplo\(\PageIndex{1}\): Velocity Autocorrelation Function for Gas

Analicemos un gas diluido de moléculas que tienen una distribución de velocidades Maxwell—Boltzmann. Nos enfocamos en el componente de la velocidad molecular a lo largo de la\(\hat{x}\) dirección,\(x_v\). Sabemos que la velocidad promedio es\(\left\langle v _ {x} \right\rangle = 0\). La función de correlación de velocidad es

\[C _ {v _ {x} v _ {x}} ( \tau ) = \left\langle v _ {x} ( \tau ) v _ {x} ( 0 ) \right\rangle \nonumber \]

Desde el principio de equipartición la energía traslacional promedio es

\[\frac {1} {2} m \left\langle v _ {x}^{2} \right\rangle = k _ {B} T / 2 \nonumber\]

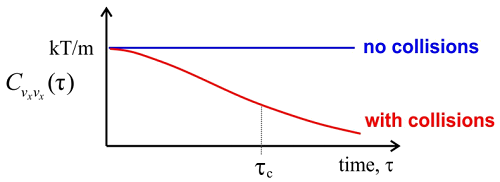
Para escalas de tiempo cortas en comparación con colisiones entre moléculas, la velocidad de cualquier molécula dada permanece constante y sin cambios, por lo que la función de correlación para la velocidad también se mantiene sin cambios en\(k_BT/m\). Este régimen de no interacción corresponde al comportamiento de un gas ideal.

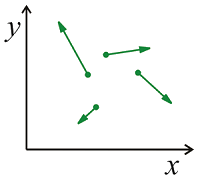
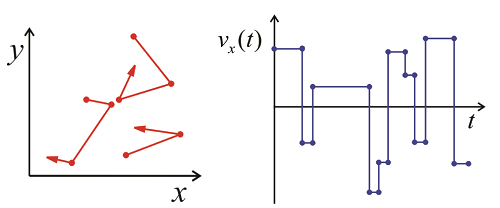
Para cualquier gas real, habrá colisiones que aleatorizan la dirección y velocidad de las moléculas, de manera que cualquier molécula durante un tiempo suficientemente largo tomará muestras de las diversas velocidades dentro de la distribución Maxwell—Boltzmann. A partir de la trayectoria de las velocidades x para una molécula dada podemos calcular\(C _ {v _ {x _ {x}}} ( \tau )\) usando promediado en el tiempo. La función de correlación caerá con un tiempo de correlación\(\tau_c\), que está relacionado con el tiempo medio entre colisiones. Después de suficientes colisiones, la correlación con la velocidad inicial se pierde y se\(C _ {v _ {x _ {x}}} ( \tau )\) acerca\(\left\langle v _ {x}^{2} \right\rangle = 0\). Finalmente, podemos determinar la constante de difusión para el gas, que relaciona el tiempo y el desplazamiento cuadrático medio de las moléculas:

\[\left\langle x^{2} (t) \right\rangle = 2 D _ {x} t.\nonumber\]

Desde

\[D _ {x} = \int _ {0}^{\infty} d t \left\langle v _ {x} (t) v _ {x} ( 0 ) \right\rangle\nonumber\]

tenemos

\[D _ {x} = k _ {B} T \tau _ {c} / m\nonumber\]

En los fluidos viscosos\(\tau _ {c} / m\) se llama la movilidad,\(\mu\).

Ejemplo\(\PageIndex{2}\): Dipole Moment Correlation Function

Consideremos ahora la función de correlación para el momento dipolar de una molécula diatómica polar en un gas diluido,\(\overline {\mu}\). Para un objeto rígido giratorio, podemos descomponer el dipolo en un vector de magnitud y unidad de dirección:

\[\overline {\mu} _ {i} = \mu _ {0} \cdot \hat {u}.\nonumber\]

Sabemos que\(\langle \hat {\mu} \rangle = 0\) ya que todas las orientaciones de las moléculas en fase gaseosa son igualmente probables. La función de correlación es

\[\begin{align*} C _ {\mu \mu} (t) & = \langle \overline {\mu} (t) \overline {\mu} ( 0 ) \rangle \\[4pt] & = \left\langle \mu _ {0}^{2} \right\rangle \langle \hat {u} (t) \cdot \hat {u} ( 0 ) \rangle \end{align*}\]

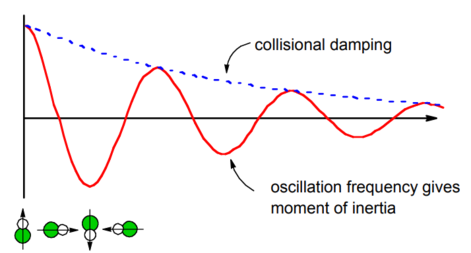
Esta función de correlación proyecta la orientación dependiente del tiempo de la molécula sobre la orientación inicial. El movimiento de rotación inercial libre conducirá a oscilaciones en la función de correlación a medida que el dipolo gira. Las oscilaciones en esta función de correlación pueden estar relacionadas con la velocidad de rotación y con ello el momento de inercia de la molécula (discutido más adelante). Cualquier amortiguación aparente en esta función de correlación reflejaría la distribución térmica de las velocidades angulares. En la práctica un gas real también tendría los efectos de amortiguación de colisiones descritos en Ejemplo\(\PageIndex{1}\) superpuestos a este proceso de relajación.

Ejemplo\(\PageIndex{3}\): Harmonic Oscillator Correlation Function

El movimiento dependiente del tiempo de un modo vibratorio armónico viene dado por la ley de Newton en términos de la aceleración y la fuerza restauradora como\(m \ddot {q} = - \kappa q\) o\(\ddot {q} = - \omega^{2} q\) donde está la constante de fuerza\(\kappa = m \omega^{2}\). Podemos escribir una solución común a esta ecuación como

\[q (t) = q ( 0 ) \cos \omega t\nonumber\]

Además, el teorema de equipartición dice que la energía térmica de equilibrio en un modo vibracional armónico es

\[\frac {1} {2} \kappa \left\langle q^{2} \right\rangle = \frac {k _ {B} T} {2}\nonumber\]

Por lo tanto, podemos escribir la función de correlación para la coordenada vibratoria armónica como

\[\begin{align*} C _ {q q} (t) &= \langle q (t) q ( 0 ) \rangle \\[4pt] &= \left\langle q^{2} \right\rangle \cos \omega t \\[4pt] & = \frac {k _ {B} T} {\kappa} \cos \omega t \end{align*}\]