11.1: Teoría Clásica de Respuesta Lineal

Utilizaremos la teoría de respuesta lineal como una forma de describir un observable experimental real. Específicamente esto nos dirá cómo cambia un sistema de equilibrio en respuesta a un potencial aplicado. La cantidad que describirá esto es una función de respuesta, una cantidad observable real. Pasaremos a mostrar cómo se relaciona con las funciones de correlación. En esta discusión se encuentra una observación particularmente importante. Ahora trataremos con un sistema de no equilibrio, pero mostraremos que cuando los cambios estén pequeños lejos del equilibrio, ¡las fluctuaciones de equilibrio dictan la respuesta de no equilibrio! Así, el conocimiento de la dinámica de equilibrio es útil para predecir el resultado de los procesos de no equilibrio.

Entonces, la pregunta es “¿Cómo responde el sistema si lo alejas del equilibrio?” Examinaremos el caso donde un sistema de equilibrio, descrito por un hamiltoniano\(H_0\) interactúa débilmente con un agente externo,\(V(t)\). El sistema se aleja del equilibrio por el agente externo, y el sistema absorbe energía del agente externo. ¿Cómo describimos las propiedades dependientes del tiempo del sistema? Primero tomamos el agente externo para interactuar con el sistema a través de una variable interna\(A\). Entonces el hamiltoniano para este problema viene dado por

\[H = H _ {0} - f (t) A \label{10.1}\]

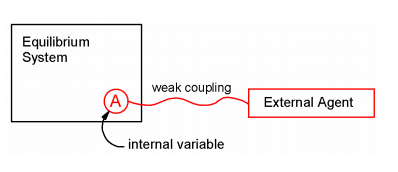
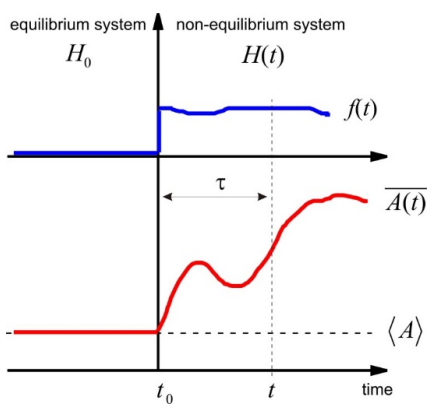
Aquí\(f(t)\) está la acción dependiente del tiempo del agente externo, y la desviación del equilibrio es lineal en la variable interna. Describimos el comportamiento de un conjunto inicialmente en equilibrio térmico asumiendo que cada miembro del conjunto está sujeto a la misma interacción con el agente externo, y luego promediando el conjunto. Inicialmente, el sistema es descrito por\(H_0\). Está en equilibrio y la variable interna se caracteriza por un promedio de conjunto de equilibrio\(\langle A \rangle\). Luego se aplica el agente externo en el tiempo t0, y el sistema se aleja del equilibrio, y se caracteriza a través de un promedio de conjunto no equilibrio,\(\overline {A}\). \(\langle A \rangle \neq \overline {A (t)}\)como resultado de la interacción.

Para una interacción débil con el agente externo, podemos describir\(\overline {A (t)}\) realizando una expansión en poderes de\(f(t)\)

\[\begin{align} \overline {A (t)} &= \left( \text {terms} f^{( 0 )} \right) + \left( \text {terms} f^{( 1 )} \right) + \ldots \label{10.2} \\[4pt] &= \langle A \rangle + \int d t _ {0} R \left( t , t _ {0} \right) f \left( t _ {0} \right) + \ldots \label{10.3} \end{align}\]

En esta expresión el agente se aplica a 0 t, y observamos el sistema att. El término principal en esta expansión es independiente de f, y por lo tanto es igual a A. El siguiente término en la Ecuación\ ref {10.3} describe la desviación del comportamiento de equilibrio en términos de una dependencia lineal del agente externo. \(R \left( t , t _ {0} \right)\)es la función de respuesta lineal, la cantidad que contiene la información microscópica del sistema y cómo responde al agente aplicado. La integración en el último término de la Ecuación\ ref {10.3} indica que el comportamiento de no equilibrio depende de la historia completa de la aplicación del agente\(f \left( t _ {0} \right)\) y de la respuesta del sistema al mismo. Estamos buscando una descripción mecánica cuántica de\(R\).

Propiedades de la función de respuesta

1. Causal: La causalidad se refiere a la observación de sentido común de que el sistema no puede responder antes de que se haya aplicado la fuerza. Por lo tanto\(R \left( t , t _ {0} \right) = 0\) para\(t < t\), y el cambio dependiente del tiempo en\(A\) es

\[\overline {\delta A (t)} = \overline {A (t)} - \langle A \rangle = \int _ {- \infty}^{t} d t _ {0} R \left( t , t _ {0} \right) f \left( t _ {0} \right) \label{10.4}\]

El límite inferior de integración se establece\(- \infty\) para reflejar que el sistema está inicialmente en equilibrio, y el límite superior es el tiempo de observación. También podemos hacer explícita la declaración de causalidad escribiendo la función de respuesta lineal con una respuesta escalonada:\(\Theta \left( t - t _ {0} \right) R \left( t , t _ {0} \right)\), donde

\[\Theta \left( t - t _ {0} \right) \equiv \left\{\begin{array} {l l} {0} & {\left( t < t _ {0} \right)} \\ {1} & {\left( t \geq t _ {0} \right)} \end{array} \right. \label{10.5}\]

2. Estacionario: Similar a nuestra discusión sobre las funciones de correlación, la dependencia del tiempo del sistema solo depende del intervalo de tiempo entre la aplicación del potencial y la observación. Por lo tanto escribimos

\[R \left( t , t _ {0} \right) = R \left( t - t _ {0} \right)\]

y

\[\delta \overline {A (t)} = \int _ {- \infty}^{t} d t _ {0} R \left( t - t _ {0} \right) f \left( t _ {0} \right) \label{10.6}\]

Esta expresión dice que la respuesta observada del sistema al agente es una convolución de la respuesta material con el tiempo-desarrollo de la fuerza aplicada. En lugar de los puntos de tiempo absolutos, podemos definir un intervalo de tiempo\(\tau = t - t _ {0}\), para que podamos escribir

\[\delta \overline {A (t)} = \int _ {0}^{\infty} d \tau R ( \tau ) f ( t - \tau ) \label{10.7}\]

3. Respuesta de impulso: Tenga en cuenta que para una perturbación de función delta:

\[f (t) = \lambda \delta \left( t - t _ {0} \right) \label{10.8}\]

Obtenemos

\[\overline {\delta A (t)} = \lambda R \left( t - t _ {0} \right) \label{10.9}\]

Así,\(R\) describe cómo se comporta el sistema cuando se aplica una perturbación abrupta y a menudo se le conoce como la función de respuesta al impulso. Una respuesta de impulso aleja al sistema del equilibrio establecido bajo H0 y, por lo tanto, la forma de una función de respuesta siempre subirá de cero y finalmente volverá a cero. En otras palabras, será una función que se puede expandir en los senos. Así, la respuesta a una f (t) arbitraria puede describirse a través de un análisis de Fourier, sugiriendo que sería útil una representación espectral de la función de respuesta.

La Susceptibilidad

El comportamiento temporal observado del sistema de no equilibrio también se puede emitir en el dominio de la frecuencia como una función de respuesta espectral, o susceptibilidad. Comenzamos con la Ecuación\ ref {10.7} y Fourier transformamos ambos lados:

\[\left.\begin{aligned} \overline {\delta A ( \omega )} & \equiv \int _ {- \infty}^{+ \infty} d t \delta \overline {A (t)} e^{i \omega t} \\ & = \int _ {- \infty}^{+ \infty} d t \left[ \int _ {0}^{\infty} d \tau R ( \tau ) f ( t - \tau ) \right] e^{i \omega t} \end{aligned} \right. \label{10.10}\]

Ahora insertamos\(e^{- i \omega \tau} e^{+ i \omega \tau} = 1\) y recogemos términos para dar

\[ \begin{align} \delta \overline {A ( \omega )} &= \int _ {- \infty}^{+ \infty} d t \int _ {0}^{\infty} d \tau R ( \tau ) f ( t - \tau ) e^{i \omega ( t - \tau )} e^{i \omega \tau} \label{10.11} \\[4pt] &= \int _ {- \infty}^{+ \infty} d t^{\prime} e^{i \omega r^{\prime}} f \left( t^{\prime} \right) \int _ {0}^{\infty} d \tau R ( \tau ) e^{i \omega \tau} \label{10.12} \end{align}\]

o

\[\delta \overline {A ( \omega )} = \tilde {f} ( \omega ) \chi ( \omega ) \label{10.13}\]

En Ecuación\ ref {10.12} cambiamos variables, estableciendo\(t^{\prime} = t - \tau\). El primer término\(\tilde {f} ( \omega )\) es una representación compleja en el dominio de la frecuencia de la fuerza impulsora, obtenida de la transformada de Fourier de\(f \left( t^{\prime} \right)\). El segundo término\(\chi ( \omega )\) es la susceptibilidad que se define como la transformada de Fourier—Laplace (es decir, transformada de Fourier de un solo lado) de la función de respuesta al impulso. Es una representación en el dominio de la frecuencia de la función de respuesta lineal. El cambio entre dominios de tiempo y frecuencia muestra que una convolución de la fuerza y respuesta en el tiempo conduce al producto de la fuerza y respuesta en frecuencia. Esta es una manifestación del teorema de la convolución:

\[A (t) \otimes B (t) \equiv \int _ {- \infty}^{\infty} d \tau A ( t - \tau ) B ( \tau ) = \int _ {- \infty}^{\infty} d \tau A ( \tau ) B ( t - \tau ) = \mathcal {H}^{- 1} [ \tilde {A} ( \omega ) \tilde {B} ( \omega ) ] \label{10.14}\]

Aquí\(\otimes\) se refiere a la convolución\(\tilde {A} ( \omega ) = \mathcal {F} [ A (t) ]] \),,\(\mathcal {F}\) es una transformada de Fourier, y\(\mathcal {F}^{- 1} [ \cdots ]\) es una transformada inversa de Fourier.

Nótese que\(R(\tau)\) es una función real, ya que la respuesta de un sistema es una observable. La susceptibilidad\(\chi ( \omega )\) es compleja:

\[\chi ( \omega ) = \chi^{\prime} ( \omega ) + i \chi^{\prime \prime} ( \omega ) \label{10.15}\]

Desde

\[\chi ( \omega ) = \int _ {0}^{\infty} d \tau R ( \tau ) e^{i \omega \tau} \label{10.16}\]

Sin embargo, las contribuciones reales e imaginarias no son independientes. Tenemos

\[\chi^{\prime} = \int _ {0}^{\infty} d \tau R ( \tau ) \cos \omega \tau \label{10.17}\]

y

\[\chi^{\prime \prime} = \int _ {0}^{\infty} d \tau R ( \tau ) \sin \omega \tau \label{10.18}\]

\(\chi^{\prime}\)y\(\chi^{\prime \prime}\) son funciones pares e impares de frecuencia:

\[\chi^{\prime} ( \omega ) = \chi^{\prime} ( - \omega ) \label{10.19}\]

\[\chi^{\prime \prime} ( \omega ) = - \chi^{\prime \prime} ( - \omega ) \label{10.20}\]

para que\[\chi ( - \omega ) = \chi^{*} ( \omega ) \label{10.21}\]

Observe también que la Ecuación\ ref {10.21} nos permite escribir

\[\chi^{\prime} ( \omega ) = \frac {1} {2} [ \chi ( \omega ) + \chi ( - \omega ) ] \label{10.22}\]

\[\chi^{\prime \prime} ( \omega ) = \frac {1} {2 i} [ \chi ( \omega ) - \chi ( - \omega ) ] \label{10.23}\]

Relaciones Kramers-Krönig

Ya que son coseno y transformadas sinusoidales de la misma función, no\(\chi^{\prime} ( \omega )\) es independiente de\(\chi^{\prime \prime} ( \omega )\). Los dos están relacionados por las relaciones Kramers-Krönig:

\[\begin{align} \chi^{\prime} ( \omega ) &= \frac {1} {\pi} P \int _ {- \infty}^{+ \infty} \frac {\chi^{\prime \prime} \left( \omega^{\prime} \right)} {\omega^{\prime} - \omega} d \omega^{\prime} \label{10.24} \\[4pt] \chi^{\prime \prime} ( \omega ) &= - \frac {1} {\pi} P \int _ {- \infty}^{+ \infty} \frac {\chi^{\prime} \left( \omega^{\prime} \right)} {\omega^{\prime} - \omega} d \omega^{\prime} \label{10.25} \end{align}\]

Estos se obtienen sustituyendo la transformada sinusoidal inversa de la Ecuación\ ref {10.18} por la Ecuación\ ref {10.17}

\[\begin{align} \chi^{\prime} ( \omega ) &= \frac {1} {\pi} \int _ {0}^{\infty} d t \cos \omega t \int _ {- \infty}^{+ \infty} \chi^{\prime \prime} \left( \omega^{\prime} \right) \sin \omega^{\prime} t d \omega^{\prime} \\[4pt] &= \frac {1} {\pi} \lim _ {L \rightarrow \infty} \int _ {- \infty}^{+ \infty} d \omega^{\prime} \chi^{\prime \prime} \left( \omega^{\prime} \right) \int _ {0}^{L} \cos \omega t \sin \omega^{\prime} t \,d t \end{align}\]

El uso de\(\cos a x \sin b x=\frac{1}{2} \sin (a+b) x+\frac{1}{2} \sin (b-a) x\) esto se puede escribir como

\[\chi^{\prime} ( \omega ) = \frac {1} {\pi} \lim _ {L \rightarrow \infty} \mathrm {P} \int _ {- \infty}^{+ \infty} d \omega^{\prime} \chi^{\prime \prime} ( \omega ) \frac {1} {2} \left[ \frac {- \cos \left( \omega^{\prime} + \omega \right) L + 1} {\omega^{\prime} + \omega} - \frac {\cos \left( \omega^{\prime} - \omega \right) L + 1} {\omega^{\prime} - \omega} \right] \label{10.27}\]

Si elegimos evaluar el límite\(L \rightarrow \infty\), los términos coseno son difíciles de tratar, pero esperamos que desaparezcan ya que oscilan rápidamente. Esto equivale a promediar sobre un campo monocromático. Alternativamente, podemos promediar en un solo ciclo:\(L=2 \pi /\left(\omega^{\prime}-\omega\right)\) para obtener eq. (10.24). La otra relación se puede derivar de manera similar. Nótese que las relaciones Kramers-Krönig son consecuencia de la causalidad, que dictan el límite inferior de\(T_{tinitial}=0\) sobre la primera integral evaluada anteriormente.

Ejemplo\(\PageIndex{1}\): Driven Harmonic Oscillator

Se puede modelar clásicamente la absorción de luz a través de una interacción resonante del campo electromagnético con un dipolo oscilante, usando las ecuaciones de Newton para un oscilador armónico amortiguado forzado:

\[\ddot {x} - \gamma \dot {x} + \omega _ {0}^{2} x = F (t) / m \label{10.28}\]

Aquí la\(x\) es la coordenada que se\(\gamma\) está impulsando, es la constante de amortiguación, y\(\omega_{0}=\sqrt{k / m}\) es la frecuencia natural del oscilador. Originalmente resolvimos este problema es tomar la fuerza impulsora para tener la forma de una fuente oscilante monocromática

\[F (t) = F _ {0} \cos \omega t \label{10.29}\]

Entonces, Ecuación\ ref {10.28} tiene la solución

\[x (t) = \frac {F _ {0}} {m} \left( \left( \omega^{2} - \omega _ {0}^{2} \right)^{2} + \gamma^{2} \omega^{2} \right)^{- 1 / 2} \sin ( \omega t + \delta ) \label{10.30}\]

con

\[\tan \delta = \omega _ {0}^{2} - \omega^{2} / \gamma \omega \label{10.31}\]

Esto demuestra que el oscilador accionado tiene un período de oscilación que es dictado por la frecuencia de accionamiento\(\omega\), y cuya amplitud y desplazamiento de fase con relación al campo de conducción viene dictado por su desintonización de la resonancia. Si hacemos un ciclo promedio para obtener la potencia absorbida promedio del campo, el espectro de absorción es

\[\begin{align*} P _ {a v g} ( \omega ) &= \langle F (t) \cdot \dot {x} (t) \rangle \label{10.32} \\[4pt] &= = \frac {\gamma \omega^{2} F _ {0}^{2}} {2 m} \left[ \left( \omega _ {0}^{2} - \omega^{2} \right)^{2} + \gamma^{2} \omega^{2} \right]^{- 1 / 2} \end{align*}\]

Para determinar la función de respuesta para el oscilador armónico amortiguado, buscamos una solución a la Ecuación\ ref {10.28} usando una fuerza impulsora impulsiva

\[F (t) = F _ {0} \delta \left( t - t _ {0} \right) \nonumber\]

La respuesta lineal de este oscilador a una fuerza arbitraria es

\[x (t) = \int _ {0}^{\infty} d \tau R ( \tau ) F ( t - \tau ) \label{10.33}\]

de manera que la dependencia del tiempo con una fuerza impulsora impulsiva es directamente proporcional a la función de respuesta,\(x(t)=F_{0} R(t)\). Para este caso, obtenemos

\[R ( \tau ) = \frac {1} {m \Omega} \exp \left( - \frac {\gamma} {2} \tau \right) \sin \Omega \tau \label{10.34}\]

La frecuencia reducida se define como

\[\Omega = \sqrt {\omega _ {0}^{2} - \gamma^{2} / 4} \label{10.35}\]

A partir de esto, evaluamos la eq. (10.16) y obtenemos la susceptibilidad

\[\chi ( \omega ) = \frac {1} {m \left( \omega _ {0}^{2} - \omega^{2} - i \gamma \omega \right)} \label{0.36}\]

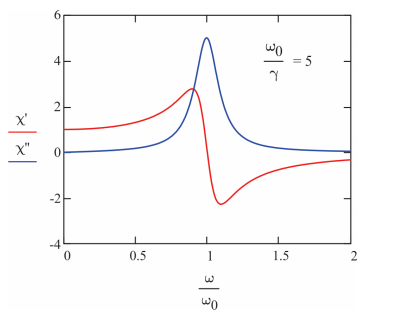
Como veremos en breve, la absorción de luz por el oscilador es proporcional a la parte imaginaria de la susceptibilidad

\[\chi^{\prime \prime} ( \omega ) = \frac {\gamma \omega} {m \left[ \left( \omega _ {0}^{2} - \omega^{2} \right)^{2} + \gamma^{2} \omega^{2} \right]} \label{10.37}\]

La parte real es

\[\chi^{\prime} ( \omega ) = \frac {\omega _ {0}^{2} - \omega^{2}} {m \left[ \left( \omega _ {0}^{2} - \omega^{2} \right)^{2} + \gamma^{2} \omega^{2} \right]} \label{10.38}\]

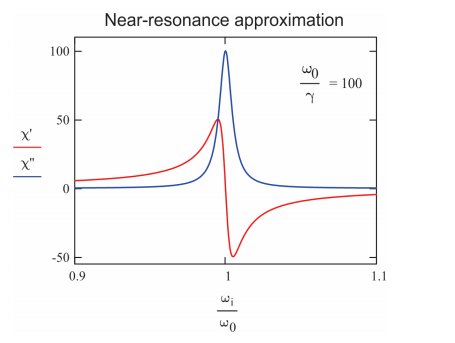
Para el caso de amortiguamiento débil que\(\gamma < < \omega _ {0}\) se encuentra comúnmente en la espectroscopia molecular, la Ecuación\ ref {10.36} se escribe como un lineshape lorentziano usando la aproximación de resonancia cercana

\[\omega^{2} - \omega _ {0}^{2} = \left( \omega + \omega _ {0} \right) \left( \omega - \omega _ {0} \right) \approx 2 \omega \left( \omega - \omega _ {0} \right) \label{10.39}\]

\[\chi ( \omega ) \approx \frac {1} {2 m \omega _ {0}} \frac {1} {\omega - \omega _ {0} + i \gamma / 2} \label{10.40}\]

Entonces la parte imaginaria de la susceptibilidad muestra una forma de línea asimétrica con un ancho de línea de ancho\(\gamma\) completo a la mitad del máximo.

\[\chi^{\prime \prime} ( \omega ) \approx \frac {1} {2 m \omega _ {0}} \frac {\gamma} {\left( \omega - \omega _ {0} \right)^{2} + \gamma^{2} / 4} \label{10.41}\]

\[\chi^{\prime} ( \omega ) \approx \frac {1} {m \omega _ {0}} \frac {\left( \omega - \omega _ {0} \right)} {\left( \omega - \omega _ {0} \right)^{2} + \gamma^{2} / 4} \label{10.42}\]

Funciones de respuesta no lineal

Si el sistema no responde de manera linealmente proporcional al potencial aplicado pero sigue siendo perturbador, podemos incluir términos no lineales, es decir, órdenes de expansión superiores de\(\overline {A (t)}\) en la Ecuación\ ref {10.3}.

Veamos segundo orden:

\[\delta \overline {A (t)}^{( 2 )} = \int d t _ {1} \int d t _ {2} R^{( 2 )} \left( t ; t _ {1} , t _ {2} \right) f _ {1} \left( t _ {1} \right) f _ {2} \left( t _ {2} \right) \label{10.43}\]

Nuevamente nos estamos integrando a lo largo de toda la historia de la aplicación de dos fuerzas\(f_1\) y\(f_2\), incluyendo cualquier dependencia cuadrática de las mismas\(f\). En este caso, haremos valer la causalidad a través de un ordenamiento de tiempo que requiera

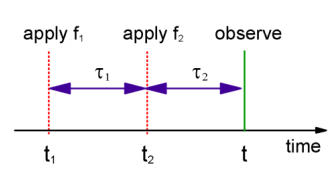
1. que todas las fuerzas deben aplicarse antes de que se observe una respuesta y
2. que la aplicación de\(f_2\) debe seguir\(f_1\). Eso es\(t \geq t _ {2} \geq t _ {1}\) o

\[R^{( 2 )} \left( t ; t _ {1} , t _ {2} \right) \Rightarrow R^{( 2 )} \cdot \Theta \left( t - t _ {2} \right) \cdot \Theta \left( t _ {2} - t _ {1} \right) \label{10.44}\]

lo que lleva a

\[\delta \overline {A (t)}^{( 2 )} = \int _ {- \infty}^{t} d t _ {2} \int _ {- \infty}^{t _ {2}} d t _ {1} R^{( 2 )} \left( t ; t _ {1} , t _ {2} \right) f _ {1} \left( t _ {1} \right) f _ {2} \left( t _ {2} \right) \label{10.45}\]

Ahora llamaremos al sistema estacionario para que solo nos preocupen los intervalos de tiempo entre tiempos de interacción consecutivos. Si definimos los intervalos entre interacciones adyacentes

\[ \left. \begin{array} {l} {\tau _ {1} = t _ {2} - t _ {1}} \\ {\tau _ {2} = t - t _ {2}} \end{array} \right. \label{10.46} \]

Entonces tenemos

\[\delta \overline {A (t)}^{( 2 )} = \int _ {0}^{\infty} d \tau _ {1} \int _ {0}^{\infty} d \tau _ {2} R^{( 2 )} \left( \tau _ {1} , \tau _ {2} \right) f _ {1} \left( t - \tau _ {1} - \tau _ {2} \right) f _ {2} \left( t - \tau _ {2} \right) \label{10.47}\]

Lecturas

1. Berna, B. J., Propedades dependientes del tiempo de los medios condensados. En Química Física: Un Tratado Avanzado, Vol. VIIIB, Henderson, D., Ed. Prensa Académica: Nueva York, 1971.
2. Berna, B. J.; Pecora, R., Dispersión dinámica de luz. R. E. Krieger Publishing Co.: Malabar, FL, 1990.
3. Chandler, D., Introducción a la Mecánica Estadística Moderna. Oxford University Press: Nueva York, 1987.
4. Mazenko, G., Mecánica Estadística de No Equilibrio. Wiley-VCH: Weinheim, 2006.
5. Sluchter, C. P., Principios de Resonancia Magnética, con Ejemplos de Física de Estado Sólido. Harper & Row: Nueva York, 1963.
6. Wang, C. H., Espectroscopia de Medios Condensados: Dinámica de Interacciones Moleculares. Prensa Académica: Orlando, 1985.
7. Zwanzig, R., Mecánica Estadística de No Equilibrio. Oxford University Press: Nueva York, 2001.

Colaboradores y Atribuciones

• Template:ContribTokmakoff